EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 30 / No 2 (April 2025) Wuhan Univ. J. Nat. Sci., 30 2 (2025) 184-194 Full HTML
Open Access
Issue
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 2, April 2025
Page(s) 184 - 194
DOI https://doi.org/10.1051/wujns/2025302184
Published online 16 May 2025

© Wuhan University 2025

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

0 Introduction

The rapid advancement of information technology and the increasing complexity of software systems have amplified the impact of defects in critical code. Mechanized theorem proving, a formal verification technique, is highly valued for its strong abstraction and logical reasoning capabilities, providing rigorous assurance of algorithmic correctness[1-2]. Functional programming, which avoids the use of global variables and assignments, eliminates execution "side effects" and reduces uncertainties in algorithm implementation[3]. These advantages have contributed to its increasing popularity in the software industry.

Multi-pattern matching algorithms are crucial in fields such as information retrieval, intrusion detection, and medicine, where efficiency and accuracy are paramount[4]. However, implementing these algorithms in mixed Chinese-English environments is challenging due to the diversity in encoding rules, including Chinese double-byte encoding, English single-byte encoding, and the differences between simplified and traditional Chinese characters. As a result, developing algorithms for such mixed environments remains a persistent challenge.

Many scholars have studied multi-pattern matching algorithms in different environments. Algorithms designed for single-language environments include Aho-Corasick (AC)[5], Deterministic Finite State Automaton (DFSA)-Quick Search (QS)[6], Improved Deterministic Finite State Automaton (IDFSA)-QS[7], etc. However, when applied to mixed environments, these algorithms often face issues such as space expansion and byte misalignment. While algorithms such as Hash Table (HT)-QS[8] and Threaded Hash Trie (THT)[9] are suited for mixed environments, and they can only be validated through experimental testing. The aforementioned approaches cannot fundamentally guarantee correctness, often leading to overlooked issues that affect the final outcomes. For example, the THT algorithm contains a variable iteration error.

In this paper, we represent the HashTrie structure as a functional framework using the interactive theorem-proving tool Isabelle/HOL, addressing the space expansion problem in mixed Chinese-English environments. We propose a functional algorithm framework based on the HashTrie structure and provide the first mechanical verification of its correctness in Isabelle/HOL. This framework is applicable to multi-pattern string indexing, string sorting, and other related tasks. The Functional Multi-Pattern Matching (FMPM) algorithm, proposed based on this framework, simplifies the implementation of the THT algorithm, effectively reducing the uncertainties factors in the transition from algorithm description to code implementation and identifies and corrects an array out-of-bounds error present in the THT algorithm.

The main contributions of this paper are:

(1) The extension of the Trie structure to propose a HashTrie-based functional framework designed for fast multi-pattern string indexing in mixed-language environments.

(2) Mechanical verification of the framework’s correctness in Isabelle/HOL, including necessary auxiliary lemmas to ensure its proper application in mixed-environment algorithms.

(3) The design of the FMPM algorithm, which addresses space expansion issues in mixed Chinese-English environments, simplifies the THT algorithm, and corrects an previously identified error.

1 Related Work

Multi-pattern matching aims to identify all substrings in texts that match a given set of patterns, but varying character encodings pose challenges. Recent research has developed algorithms for specific environments.

In single-language contexts, such as Chinese or English, the DFSA algorithm builds a DFA using a Hash table for state transitions. This approach requires space proportional to Num(state) × 256 for single-byte characters[5]. Ref.[6] enhanced matching efficiency by splitting Chinese characters into high and low bytes and using a Trie with QS. Ref. [10] optimized the space efficiency of the AC algorithm by employing hash functions for pattern prefixes and bit vectors for storage. Ref.[7] advanced time performance by constructing a state machine that splits Chinese encodings and creates a failure transition table based on encoding associations. These algorithms work well in single-language environments, but they encounter significant challenges when applied in mixed environments. (1) In double-byte Chinese contexts, the memory usage for state transition Hash tables can expand up to 256 times as high as that in single-byte English contexts, leading to a rapid memory expansion. (2) ASCII single-byte encoding for English and double-byte encoding for Chinese can cause byte misinterpretation, resulting in errors.

In multi-pattern matching algorithms for mixed Chinese-English environments, Ref.[4] introduced a Hash-based multi-pattern matching algorithm that utilizes word units and jump mechanisms to improve efficiency, though it may miss or incorrectly match patterns[9]. Ref.[11] proposed the Height Optimized Trie (HOT) structure, which merges nodes in a Binary Patricia Trie and limits fan-out to optimize memory usage and retrieval. Refs.[8, 9, 12] analyzed the performance of multi-pattern matching algorithms in mixed Chinese-English environments. The THT algorithm is efficient but prone to out-of-bounds errors, leading to potential issues[13].

Mechanical verification ensures program correctness by using mathematical logic across all execution scenarios[3]. Ref.[14] used Lisp to prove the correctness of the Boyer-Moore single-pattern matching algorithm[15]. Refs.[16-17] proposed a lock-free Hash Trie based on the Hash Array Mapped Trie (HAMT) [18], verifying its linearizability and lock-freeness through manual validation. Ref.[19] modeled and verified a Trie structure in Isabelle but highlighted significant redundancy in the process. Ref.[20] introduced the Trie+ structure, which reduces storage space by 50% and provides rigorous mechanized verification. While proof assistants have been used to validate complex systems, prior research has primarily focused on single-pattern matching algorithms, leaving a gap in the mechanized verification of multi-pattern matching algorithms.

This paper proposes a functional HashTrie framework verified in Isabelle/HOL for mixed-language environments. Based on this framework, the FMPM algorithm optimizes the THT algorithm, enhances Chinese-English matching precision, and corrects a out-of-bounds error.

2 Functional Framework Based on HashTrie Structure and Its Mechanical Verification

The Trie tree is efficient for string lookup but is limited to single-language environments. This section introduces a functional framework using the HashTrie structure, which replaces the associative table with a complete Hash table. This approach allows storing string information from mixed-language environments within a single HashTrie, thereby enhancing compatibility and improving the lookup speed. The framework supports quick multi-pattern indexing and string sorting in mixed-language environments and has undergone mechanized verification in Isabelle/HOL to ensure its accuracy and efficiency.

2.1 Definition of Trie Structure for Single Environments

In a Trie tree, string information is stored in terminal nodes, while many nodes remain empty. To address this situation, the option monad encapsulates the string information. Each node uses an associative table to map keys to sub-Tries, which guides the search to the next subtree. The option monad and Trie tree are defined as follows:

datatype 'v option = None | Some 'v

datatype ('a,'v)trie = Trie " 'v option" "('a * ('a,'v)trie) list"

In a Trie tree, the type parameter 'a for string characters cannot be used for multiple types simultaneously, which limits it to a single environment. For example, Fig. 1 shows a Trie for English strings {black, blue, slow, some, sure}. When conducting a search, each character must be looked up in the associative table of each node.

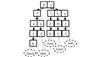thumbnail Fig. 1 Trie tree

2.2 Definition of the HashTrie Structure for Mixed Environments

In a mixed environment, a set of patterns contains at least two types of characters. A Trie tree cannot store these diverse types of patterns simultaneously. By utilizing character encoding rules (ASCII for English character, GB2312 for Simplified Chinese character, and Big5 for Traditional Chinese character), patterns are converted into consistent encoded strings. This enables unified handling of different string types.

ASCII uses the encoding range from 0 to 127, primarily representing English characters. GB2312 is compatible with ASCII within the range of 0 to 127, while the range from 0xA0 to 0xFE is designated for representing Chinese characters. The Big5 encoding, which is predominantly used for traditional Chinese characters, has a different encoding range from both ASCII and GB231. Therefore, the encoding ranges of these three encoding schemes do not overlap, allowing them to coexist in the same text without causing any conflicts.

Definitions and theorems for multi-pattern matching in such environments are provided below.

Definition 1   (Encoded String and Encoded Type) Both single-byte and double-byte characters can be represented in their encoded forms.

For instance, the Chinese characters "复" "兴" "之" "路" are encoded as 0xB8B4, 0xD0CB, 0xD6AE, and 0xC2B7, respectively. Splitting these bytes yields the encoded string [B8, B4, D0, CB, D6, AE, C, B7]. Converting these bytes to decimal results in a unified encoded type "nat".

Definition 2   (Matching Machine) A matching machine organizes multiple patterns to efficiently find all matching substrings in any given text.

The Trie tree in Fig.1 is an example of such a matching machine.

Definition 3   (One-Pass Matching) One-pass matching means starting a match from any position in a text and continuing until the match either succeeds or fails.

To address the issue of storing different pattern types, we introduce the HashTrie structure. It extends the Trie by replacing the associative table with a Hash table, enabling more efficient lookups. The Hash table’s index number acts as the key, and the table stores the corresponding sub-Trie. The HashTrie structure is defined as follows:

datatype 'v hashtrie = Trie " 'v option" " 'v hashtrie list"

A HashTrie matching machine uses a complete Hash table of size 256 as a node. The encoded character of the string serves as the key in the Hash table and maps to the corresponding sub-Trie. All Hash tables within the HashTrie structure are set to size 256, matching the range of single-byte values. Therefore, when searching strings with a HashTrie matching machine, there is no need for traversal or additional hash functions, resulting in high search efficiency. Additionally, after converting a string into an encoded string, a single-byte character can be represented by a single node, and a double-byte character can be represented by two adjacent nodes. For example, the Chinese character "复" has an encoded value of "0xB8B4", and its corresponding node in the HashTrie tree is shown in Fig. 2.

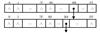thumbnail Fig. 2 The node representing "复"

The HashTrie matching machine effectively handles strings with both single-byte and double-byte encodings. Once all strings in the pattern set are converted into encoded strings, both single-byte and double-byte encoded patterns can be stored in the same HashTrie matching machine. Figure 3 illustrates the HashTrie matching machine for the mixed-environment pattern set {black, blue, 伟大复兴, 伟大梦想}. The encoded values for the characters "伟" "大" "复" "兴" "梦", and "想" are 0xCEB0, 0xB4F, 0xB8B4, 0xD0CB, 0xC3CE, and 0xCFEB, respectively.

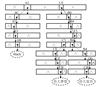thumbnail Fig. 3 Example diagram of the HashTrie matching machine

2.3 Functional Construction Framework of the HashTrie Matching Machine

Specifically, the Trie tree is constructed using the update function, which adds string information to the tree. The update function depends on the "assoc" function[21], which manages the mapping between keys and their corresponding sub-Tries. For a given key, the "assoc" function searches the association table and returns the matching sub-Trie. The update function for the Trie tree is defined as follows:

The update function in a Trie tree constructs the structure for single-environment strings, using the inefficient "assoc" function to search for subtrees, which makes it difficult to access the old subtrees afterward[21]. Similarly, the HashTrie matching machine is constructed with the "ht_update" function, which adds string information to the HashTrie. The "ht_update" function is defined as follows:

The "ht_update" function introduces an additional condition compared to the update function, handling subtrees based on the input sequence as follows:

(1) If the matching machine t lacks the prefix x (the first character of the new string x#xs) and the string has more than one element, the subtree tt is (Trie va hashtrie_node), where hashtrie_node is an empty Hash table for the remaining string xs.

(2) If t lacks a prefix x, and the new string has only one element, the extracted subtree tt is (Trie va []), where [] indicates no further elements to store.

(3) If t contains a prefix x with at least one element, tt is retrieved from at = (alist t)!x.

The "ht_update" function constructs the HashTrie matching machine using a complete Hash table, indexing characters by their code to find and update subtrees recursively. This approach can efficiently handles both single and double-byte characters, improving search performance and maintaining easy access to old subtrees.

primrec update:: "('a, 'v)trie ⇒ 'a list ⇒ 'v ⇒ ('a, 'v) trie"
where "update t [] v = Trie (Some v) (alist t)" |"update t (a#as) v = (let tt = (case assoc (alist t) a of None ⇒ Trie None [] |
Some at ⇒ at) in Trie (value t) ((a,update tt as v) # alist t))"
primrec ht_update::"nat list ⇒ 'v hashtrie ⇒ 'v ⇒'v hashtrie"
where "ht_update [] t v= Trie (Some v) (alist t)"|"ht_update (x # xs) t v = (let tt = (case (alist t)!x of Trie va []) ⇒ (if xs ≠ [] then Trie va hashtrie_node else Trie va []) | at ⇒ at) in Trie (value t) (alist t[x:=(ht_update xs tt v)]))"

2.4 Mechanical Proof of the Algorithm Framework

This section presents a mechanical proof of the correctness of the HashTrie structure and the matching machine construction algorithm. The proof focuses on two key properties.

(1) The algorithm is guaranteed to terminate.

(2) After updating the matching machine, the difference between the original and updated machine is the newly added pattern string.

For property (1), all the functional code presented in this paper is correctly defined using definition, primrec, or fun. The termination of the algorithm can be mechanically verified by Isabelle/HOL. Therefore, this section focuses on proving the correctness of property (2).

It has been proven that using homomorphic sets to represent specifications of data structures such as the Trie is valid[22]. To formalize property (2), an abstract set function set_ht::" 'v hashtrie ⇒ (nat list) set" is defined. Theorem 1 uses the union (∪) in sets to specify the key function ht_update of the HashTrie structure, stated as follows:

Theorem 1   upht_correct:"⋀hashtrie v. isless_hashlength new_str ht ⇒ set_ht (updata new_str ht v) = {new_str} ∪ set_ht ht".

Theorem 1   asserts that after applying ht_update, the set of strings in the matching machine ht will include the newly added string new_str, which was not in the original set. This theorem ensures the correctness of the matching machine construction. The function isless_hashlength checks whether all elements in a list are shorter in length than the HashTrie, while set_ht retrieves all strings in the machine.

Proof   The proof uses structural induction on new_str, with two parts: the base case, where new_str is empty, and the inductive case, where new_str is non-empty and requires auxiliary lemmas. Figure 4 illustrates the dependencies between Theorem 1 and these lemmas.

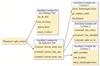thumbnail Fig. 4 The dependency between Theorem 1 and the auxiliary lemmas

The inductive part based on the definition of the ht_update function can be divided into three cases, each corresponding to Lemmas 1-3:

(1) When ht has no strings with the prefix of the first element of new_str, and new_str has at least two elements.

(2) When ht has no strings with the prefix of the first element of new_str, and new_str has only one element.

(3) When the matching machine ht contains strings with the prefix of the first element of new_str, and new_str has at least one element.

Lemma 1   newstr_more_two:" isless_hashlength (a # m) ht ⇒ m ≠ [] ⇒ alist ht ! a = Trie va h ⇒ h = [] ⇒ set_ht (Trie (value ht) (alist ht[a := ht_update m (Trie va hashtrie_node) v])) = insert (a # m) (set_ht ht)".

Lemma 1   states that if the subtree at index a in ht has no successors (h = []), then adding the string a#m with at least two elements will result in a new machine with just one more string, a#m, compared with the original.

Lemma 2   newstr_only_one:" isless_hashlength (a # m) ht ⇒ ¬ m ≠ [] ⇒ alist ht ! a = Trie va h ⇒ h = [] ⇒ set_ht (Trie (value ht) (alist ht[a := ht_update m (Trie va []) v])) = insert (a # m) (set_ht ht)".

Lemma 2   states that if the subtree at index a in ht has no successors (h = []), then adding the single-element string [a] will result in a new machine with just one additional string, [a], compared with the original.

Lemma 3   newstr_more_one: "(⋀ht v. isless_hashlength m ht ⇒ set_ht (ht_update m ht v) = insert m (set_ht ht)) ⇒ isless_hashlength (a # m) ht ⇒ h = h1 # h2 ⇒ alist ht ! a = Trie va (h1 # h2) ⇒ set_ht (Trie (value ht) (alist ht[a := ht_update m (Trie va (h1 # h2)) v])) = insert (a # m) (set_ht ht)".

Lemma 3   states that if the subtree at index a in ht has successors (h = h1 # h2), then after adding the string a # m, the new machine will contain the string a # m in addition to the original strings.

The target equation of Lemma 2 can be divided into cases where the internal code string starts with 'a' or not. When it starts with 'a', all internal code strings except for the single-element string 'a' can be mechanically verified. The remaining cases rely on auxiliary Lemmas 4 and 5.

Lemma 4   one_isless:" isless_hashlength [a] ht ⇒ a < length (alist ht)".

Lemma 5   one_isinupht:"⋀a ht v. a<length (alist ht) ⇒ (isin_ht (Trie (value ht) (alist ht[a := Trie (Some v) []]))) [a]".

When the string starts with 'a', the target equation in Lemma 2 can be automatically divided into two implications. The left side implying the right side is more specific and requires the introduction of auxiliary Lemma 6.

Lemma 6   upht_to_ht:"x = aa#as ⇒ x ≠ [a] ⇒ isless_hashlength [a] ht ⇒isin_ht (Trie (value ht) (alist ht[a := Trie (Some v) []])) x ⇒ isin_ht ht x".

The base case of Theorem 1, with new_str=[], is verified in Isabelle/HOL. The inductive step is proven using Lemmas 1-3. This confirms Theorem 1. The proof process of Theorem 1 is shown in Fig. 5.

thumbnail Fig. 5 Proof of correctness for the functional framework of HashTrie structures in Isabelle/HOL

3 FMPM Algorithm for Mixed Chinese and English Environment

The THT algorithm for mixed Chinese and English environments was only validated through testing. This approach may overlook hidden errors, such as array out-of-bounds issues caused by unverified remaining characters[9].

In this section, a HashTrie matching machine for mixed Chinese and English environments is developed using the framework presented in the previous section . Unlike jump-based algorithms, the HashTrie-based multi-pattern matching algorithm prevents missed or incorrect matches. By preprocessing the pattern set, it calculates the next match scenario, creating a threaded HashTrie that improves efficiency by avoiding backtracking and array out-of-bounds errors.

3.1 Multi-Pattern Matching Algorithm for Mixed Chinese and English Based on HashTrie Structure

To enhance efficiency, the first characters of pattern strings are stored in a complete Hash table. This is because the first character of a Chinese string often leads to mismatches. Matching only proceeds to the subsequent substrings after a successful first-character match. The Hash table consists of 256 tables of size 256, indexed by the high and low bytes of a Chinese character’s code or an English character’s code.

It is important to note that the rows and columns of the first-character Hash table correspond to the code of the first character in the pattern string. English character pattern strings are stored at the main diagonal position of the first-character Hash table. Based on the HashTrie construction algorithm in Section 2.4, after instantiating the type parameter 'v in the ht_update function as a string representing string information, a HashTrie construction function for a mixed Chinese and English environment can be defined as follows:

Theorem 2   In a mixed-language environment, multi-pattern matching algorithms based on jump matching may skip some characters in the text string, potentially leading to missed or incorrect matches.

Ref.[9] provided Theorem 2 and its proof, stating that the HashTrie-based multi-pattern matching algorithm advances by a single character regardless of whether the match is successful. This brute-force approach avoids missed or incorrect matches but may result in redundant character processing, thus reducing efficiency. Given a fixed pattern set, the relationship between the matched segments of one pattern and those of others can determine the subsequent matching states. Section 3.2 will discuss the Threaded HashTrie algorithm for computing the next match.

primrec head_hash_table::"nat list list ⇒ string list ⇒ (string hashtrie) list list ⇒ (string hashtrie) list list"
where " head_hash_table [] vs h = h"|" head_hash_table (x#xs) vs h = (let l = (if ((x!0)>128) then x else (x!0)#x) in
head_hash_table xs (tl vs) (uphead l h (hd vs)))"

3.2 Functional Construction Algorithm for the Threaded HashTrie Matching Machine

Based on the HashTrie matching machine from Section 3.1, the threaded HashTrie matching machine algorithm computes the next match after each successful match of a pattern string. This approach improves efficiency by avoiding repeated matching, a limitation in brute-force algorithms. The algorithm includes three operations: subtree lookup, threading for failed matches, and threading for successful matches.

For example, Fig.6 illustrates the threaded HashTrie matching machine and the relationships among the three operations, based on the code list corresponding to the pattern set {民族伟大复兴, 伟大梦想, 复兴之路}.

thumbnail Fig. 6 Threaded HashTrie matching machine and the relationships among the three operations

In the string "民族伟大复兴", the substring "伟大" can serve as a prefix for the string "伟大梦想". The subtree operation locates the subtree for the prefix "伟大", corresponding to the substring "梦想". If the matching fails at the 5th character "复", the algorithm skips to the substring "梦想" in "伟大梦想" to continue matching. This is the result of the failure thread for the character "复". Similarly, if the matching succeeds, it proceeds to the substring "之路" in "复兴之路". The results of the failure and success threads are stored in two lists whose lengths are equal to that of the pattern strings. The jump targets are found through the subtree operation. The functional implementations of the subtree lookup, failure threading, and success threading operations are as follows:

(1) Subtree lookup

The function find_p locates the next matching situation based on the already matched part. It searches for the corresponding subtree in the matching machine for a substring prefix. The find_p function does not consider the pattern’s first character. The find_prefix function, which accounts for the first character, finds the corresponding matching machine in the first-character Hash table using the character’s code. Then, it locates the subtree with the given prefix within the matching machine. The function definitions are as follows:

(2) Threading for match failure

The threading process considers both Chinese and English pattern strings, requiring separation the first character from the subsequent substring. The function c_findex_line, which handles threading for match failure Chinese pattern strings, is provided below.

In a Chinese environment, the function c_findex_line handles threading for match failure by identifying the appropriate position of the pattern's initial character in the Hash table and determining the threading results for subsequent failures. The English function (e_findex_line) is similar but simpler, so it is not discussed in detail.

The findex function calculates the threading results for each character position Chinese-English pattern strings using the c_findex_line/e_findex_line functions based on the character attributes of the pattern. The implementation of the findex function is as follows:

(3) Threading for match success

The function sindex, which computes the threading position when a pattern matches successfully, is defined in a similar way to the failure function findex. However, in the case of a successful match, only the position of the last character in the pattern is considered. In both Chinese and English environments, the index position is calculated only when all bytes match successfully. The main function for threading on a successful match for Chinese patterns is c_sindex_l, defined below:

A threaded HashTrie matcher is composed of a HashTrie matcher for the pattern set and two lists that store jump information for successful or failed matches. The indices in these lists correspond directly to the indices of the codes in the encoded string.

primrec find_p::"nat list ⇒ string hashtrie ⇒ string hashtrie option"
where "find_p [] t = Some t"| "find_p (x#xs) t = (if alist t = [] then None else (case (alist t)!x of Trie None [] ⇒ None |
Trie _ _ ⇒ find_p xs ((alist t)!x)))"
definition find_prefix::"nat list ⇒ (string hashtrie) list list ⇒ string hashtrie option"
where "find_prefix k h = (case k of (x#xs) ⇒ (if (x > 128) then find_p (tl xs) (h!x!(hd xs)) else find_p xs (h!x!x)))"
definition c_findex_line::"nat list ⇒ nat list list ⇒ (string hashtrie) list list ⇒ (nat × string hashtrie) list"
where "c_findex_line k ks h = (case k of x#s#xs ⇒ c_findex_l (drop 2 xs) (take 2 xs) ks [(0, Trie None []), (0, Trie None []), (0, Trie None []), (0, Trie None [])] h)"
primrec findex::"nat list list ⇒ nat list list ⇒ (nat × string hashtrie) list list ⇒ (string hashtrie) list list ⇒ (nat × string hashtrie) list list"
where "findex [] ks f h = f"| "findex (x#xs) ks f h =(let l = (if (hd x) > 128 then(f@[(c_findex_line x (ks@xs) h)]) else
(f@[(e_findex_line x (ks@xs) h)])) in findex xs (ks@[x]) l h)"
fun c_sindex_l::"nat list ⇒ nat list ⇒ nat list list ⇒ (nat list × string hashtrie) list ⇒ (string hashtrie) list list ⇒ (nat list × string hashtrie) list "
where "c_sindex_l (x#m#xs) p ks s h = c_sindex_l xs (p@[x,m]) ks (s@[([], Trie None []),([], Trie None [])]) h"
"c_sindex_l [] p ks s h = (let i =
(case c_common_pre_suf p ks of None ⇒ ([], Trie None [])| Some n ⇒ (n, the (find_prefix n h))) in (butlast s@[i]))"

3.3 Mixed Chinese-English Multi-Pattern Matching Algorithm Based on Threaded HashTrie Structure

The threaded HashTrie matcher obtained through the preprocessing algorithm in Section 3.2 includes two lists for handling successful and failed matches. At the end of each match, this matcher provides the next matching position. The FMPM based on the threaded HashTrie structure effectively avoids backtracking and improves matching efficiency.

For example, according to the threaded results in Fig. 7, when matching the text "民族伟大梦想和民族伟大复兴之路" against the pattern "民族伟大复兴", if the match fails at the 5th character "复", the next match should continue at the 3rd character "梦" in the pattern "伟大梦想". If the match is successful, the next match should continue at the 3rd character "之" in the pattern "复兴之路". In other cases, whether the match is successful or not, the next match commences from the character immediately following the end of the current match.

thumbnail Fig. 7 Matching process diagram

During the matching process, each character position must be checked to distinguish between Chinese and English strings. After identifying the character type, the Chinese or English multi-pattern preprocessing function is employed to match Chinese or English substrings within the text. At the end of each match, it uses the threading information list to determine the next matching position and outputs the result for the processed text.

Regarding the iteration of boundary variable, as described in Ref.[9], the THT algorithm may lead to array out-of-bounds errors when there is only one character left to be processed. Therefore, the number of remaining characters must be checked at the start of each matching iteration. If the character code is greater than 128, indicating a Chinese character, the size of xs must be ≥ 3 to ensure that at least two characters remain unmatched. If the size of xs < 3, no further matching is required when only one character remains in the Chinese text. For characters with a code ≤ 128, which indicate English characters, similar logic applies, and array out-of-bounds situations are handled through case analysis.

Based on the above, the multi-pattern matching algorithm using the threaded HashTrie is defined as follows:

The FMPM algorithm initially identifies the character type. Then, it uses the Chinese and English multi-pattern preprocessing functions to obtain the information of the matched substring and the matching results for Chinese and English text substrings. After removing the matched substring, it continues matching the remaining text.

function FMPM::"nat list ⇒ nat list list ⇒ string hashtrie list list ⇒ string list ⇒ string list"
where "FMPM [] ks h p = p"| "FMPM (x#xs) ks h p = (if x>128 ∧ length xs ≥ 3 then (case xs of (xx#a#aa#as) ⇒ (case find_p [a,aa] (h!x!xx) of None ⇒ FMPM (a#aa#as) ks h p| Some ht ⇒ (let (i, n_p) = c_FMPM as [x,xx,a,aa] ks ht (sindex ks [] [] h)
(findex ks [] [] h) p [] in FMPM (drop (length i) as) ks h n_p)))
else (if x>128 ∧ length xs < 3 then p else (case xs of [] ⇒ p| xx#as ⇒ (case find_p [xx] (h!x!x) of None ⇒ FMPM xs ks h p |
Some ht ⇒ (let (I, n_p) = e_FMPM as [x,xx] ks ht (sindex ks [] [] h) (findex ks [] [] h) p [] in (case i of FMPM (drop (length i) as) ks h n_p)))))"

3.4 The Efficiency of the Threaded FMPM Algorithm

To evaluate the efficiency of the threaded FMPM algorithm based on HashTrie, the time model proposed in Ref. [23] is used to compare the efficiency of Trie, HashTrie, and threaded HashTrie algorithms, further demonstrating the effectiveness and efficiency advantages of the HashTrie functional algorithm.

For this section, the experimental text is selected from the People’s Daily Online article "People’s Daily Commentary: National Security is of Paramount Importance, and Everyone is Responsible for Cooperating with Law Enforcement" (http://opinion.people.com.cn/n1/2024/0306/c223228-40190160.html). The full text consists of 744 characters and 1 488 bytes. Five sets of keywords (pattern sets) containing 5, 10, 15, 20, and 25 patterns were randomly selected from the article. The time model is used to calculate the matching time required by the three algorithms for the text. The specific results are shown in Fig. 8.

thumbnail Fig. 8 The comparison of execution times of various FMPM algorithms

The threaded HashTrie demonstrates a significant reduction in matching time compared with both the Trie and HashTrie structures. Specifically, across five distinct sets of pattern strings, the matching time of the threaded HashTrie averages approximately 26.41%, 17.22%, 13.55%, 11.70%, and 9.37% of the Trie-based approach, and around 88.58%, 86.78%, 82.16%, 78.96%, and 76.83% of the HashTrie-based method. These results clearly indicate that, compared with FMPM algorithms based on Trie and HashTrie frameworks, the FMPM algorithm based on threaded HashTrie demonstrates higher efficiency. Furthermore, this efficiency advantage becomes increasingly pronounced as the size of the pattern set increases.

4 Conclusion

In mixed environments with diverse character types, traditional multi-pattern matching algorithms face issues such as space expansion and byte misalignment. Classic Trie structures also struggle with handling different types of strings. The HashTrie structure, which uses character codes as keys for complete Hash tables, can manage various string types and ensures accurate lookups. The functional HashTrie framework, whose correctness has been proven using Isabelle/HOL, enables efficient indexing and sorting of multi-pattern strings. To resolve issues such as space expansion and incorrect matches, the FMPM algorithm was developed for HashTrie structures in Isabelle/HOL[24]. This algorithm improves performance and fixes errors in previous methods.

Future research could further optimize the HashTrie functional structure, especially in terms of space efficiency. Currently, this structure might lead to redundant space usage and single-path, non-branching situations when storing strings with no common prefixes. To address this, strategies such as path compression could substantially reduce memory consumption while maintaining efficient retrieval performance. Furthermore, finding a balance between space and time complexity, especially in different application scenarios, remains a subject worthy in-depth exploration. Additionally, integrating this optimized structure with our previous works[25-27] to form a tree-based framework could further enhance overall performance and enable the automation of mechanized verification. This framework not only contributes to improving efficiency but also holds the potential to advance automated research and applications in related fields.

References

  1. Lochbihler A. A mechanized proof of the max-flow min-cut theorem for countable networks with applications to probability theory[J]. Journal of Automated Reasoning, 2022, 66(4): 585-610. [Google Scholar]
  2. Wang X B, Kou M S, Li C Y, et al. Implementation of theorem prover for PPTL with indexed expressions[J]. Journal of Software, 2022, 33(6): 2172-2188(Ch). [Google Scholar]
  3. Zhao Y W. Functional Programming and Proof[EB/OL]. [2021-07-06]. https://www.yuque.com/zhaoyongwang/fpp/(Ch). [Google Scholar]
  4. Dong M, Chang Z J, Zhang R J. A multiple pattern matching algorithm for specifications of incremental metadata for sci-tech literature[J]. Data Analysis and Knowledge Discovery, 2021, 5(6): 135-144(Ch). [Google Scholar]
  5. Aho A V, Corasick M J. Efficient string matching: An aid to bibliographic search[J]. Communications of the ACM, 1975, 18(6): 333-340. [Google Scholar]
  6. Shen Z, Wang Y C, Liu G S. Improved multiple pattern algorithm for Chinese string matching[J]. Journal of the China Society for Scientific and Technical Information, 2002, 21(1): 27-32(Ch). [Google Scholar]
  7. Zhu Y Q, Qin Z G. Multi-pattern matching algorithm based on coding association[J]. Computer Science, 2016, 43(2): 26-30(Ch). [Google Scholar]
  8. Liao M T, Zhang D Y, Li J K. High efficiency Chinese-English multi-pattern match algorithm based on network processor[J]. Computer Engineering, 2007, 33(5): 38-40(Ch). [Google Scholar]
  9. Sun Q D, Huang X B, Wang Q. Multiple pattern matching on Chinese/English mixed texts[J]. Journal of Software, 2008, 19(3): 674-686(Ch). [Google Scholar]
  10. Zhang P, Liu Y B, Yu J, et al. HashTrie: A space-efficient multiple string matching algorithm[J]. Journal on Communications, 2015, 36(10): 172-180(Ch). [Google Scholar]
  11. Binna R, Zangerle E, Pichl M, et al. HOT: A height optimized trie index for main-memory database systems[C]//Proceedings of the 2018 International Conference on Management of Data. New York: ACM, 2018: 521-534. [Google Scholar]
  12. Wang Z, Li R F, Li Y B, et al. A parallel multiple pattern matching algorithm on Chinese/English mixing[J]. Computer Engineering, 2014, 40(4): 318-321(Ch). [Google Scholar]
  13. Henriksen T. Bounds checking on GPU[J]. International Journal of Parallel Programming, 2021, 49(6): 761-775. [Google Scholar]
  14. Moore J S, Martinez M. A mechanically checked proof of the correctness of the Boyer-Moore fast string searching algorithm[C]//Engineering Methods and Tools for Software Safety and Security. Marktoberdorf: IOS Press, 2009: 267-284. [Google Scholar]
  15. Boyer R S, Moore J S. A fast string searching algorithm[J]. Communications of the ACM, 1977, 20(10): 762-772. [CrossRef] [Google Scholar]
  16. Moreno P, Areias M, Rocha R. On the implementation of memory reclamation methods in a lock-free hash trie design[J]. Journal of Parallel and Distributed Computing, 2021, 155: 1-13. [Google Scholar]
  17. Areias M, Rocha R. On the correctness and efficiency of a novel lock-free hash trie map design[J]. Journal of Parallel and Distributed Computing, 2021, 150: 184-195. [Google Scholar]
  18. Atighehchi K, Rolland R. Optimization of tree modes for parallel hash functions: A case study[J]. IEEE Transactions on Computers, 2017, 66(9): 1585-1598. [Google Scholar]
  19. Lochbihler A, Nipkow T. Trie[EB/OL]. [2024-05-26]. https://www.isa-afp.org/browser_info/current/AFP/Trie/document.pdf. [Google Scholar]
  20. Zuo Z K, Ke Y H, Huang Q, et al. Trie+ structural functional modeling, mechanized verification and application[J]. Journal of Software, 2024, 35(9): 4242-4264(Ch). [Google Scholar]
  21. Nipkow T, Paulson L C, Wenzel M. A proof assistant for higher-order logic[EB/OL]. [2024-05-23]. https://isabelle.in.tum.de/dist/Isabelle/doc/tutorial.pdf. [Google Scholar]
  22. Nipkow T, Blanchette J, Eberl M. Functional algorithms, verified![EB/OL]. [2024-09-22]. https://functional-algorithms-verified.org. [Google Scholar]
  23. Zeng Z C. Modeling, Mechanized Verification, and Application of HashTrie Functional Algorithm[D]. Jiangxi: Jiangxi Normal University, 2024(Ch). [Google Scholar]
  24. Eßmann R, Nipkow T, Robillard S. Verified approximation algorithms[C]// Automated Reasoning. Cham: Springer International Publishing, 2020: 291-306. [Google Scholar]
  25. Zuo Z K, Fang Y, Huang Q, et al. Derivation and formal proof of binary tree sorting non-recursive algorithm[J]. Journal of Jiangxi Normal University (Natural Science), 2020, 44(6): 625-632(Ch). [Google Scholar]
  26. Zuo Z K, Fang Y, Huang Z P, et al. The derivation and formal proof of non-recursive algorithm for binary tree queue relation problems[J]. Journal of Jiangxi Normal University (Natural Science), 2022, 46(1): 49-58(Ch). [Google Scholar]
  27. Wang C J, He J F, Luo H M, et al. The model-driven Dafny program generation and automatic verification[J]. Journal of Jiangxi Normal University (Natural Science), 2020, 44(4): 378-384(Ch). [Google Scholar]

All Figures

thumbnail Fig. 1 Trie tree
In the text
thumbnail Fig. 2 The node representing "复"
In the text
thumbnail Fig. 3 Example diagram of the HashTrie matching machine
In the text
thumbnail Fig. 4 The dependency between Theorem 1 and the auxiliary lemmas
In the text
thumbnail Fig. 5 Proof of correctness for the functional framework of HashTrie structures in Isabelle/HOL
In the text
thumbnail Fig. 6 Threaded HashTrie matching machine and the relationships among the three operations
In the text
thumbnail Fig. 7 Matching process diagram
In the text
thumbnail Fig. 8 The comparison of execution times of various FMPM algorithms
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.