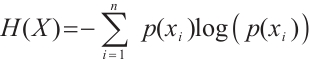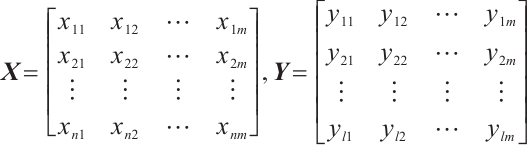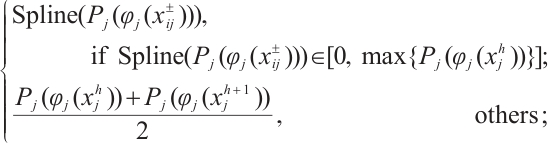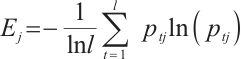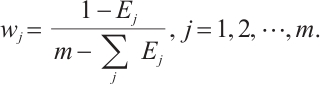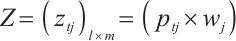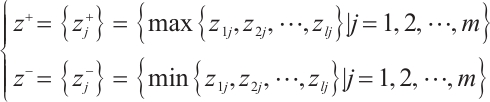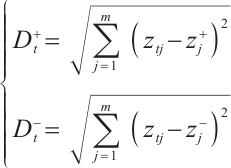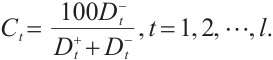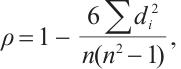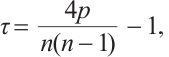© Wuhan University 2025

0 Introduction

As the environmental factor intrinsically linked to public issues and habitat, water environment has always been the focus of environmentalists' attention. To control water pollution and monitor long-term or timely changes in water environment, water quality assessment has increased enormous attention for researchers. In the past two decades, there have been many researches on how to quantitatively evaluate water quality based on the entropy theory. Ma et al^[1] merged the advantages of the Principal Component Analysis (PCA) and the information entropy (IE) to obtain the weights of indicators, which was established to assess the landscape water quality in Zhengzhou City, China. Mahjouri et al^[2] used the discrete entropy theory to assess the efficiency of the Jajrood River monitoring network and revised both the location of existing monitoring stations and temporal frequencies of data gathering. Paul et al^[3] applied information entropy to Water Quality Index (WQI) calculation and calculated the Pearson correlation matrix between different parameters for analyzing its relationship. Li et al^[4] have done a lot of research work on water quality assessment based on entropy weight theory, such as integrating entropy weight theory and WQI, applying set pair analysis method based on entropy weight^[5], and improving Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method based on entropy weight^[6-8]. Amiri et al^[9] improved WQI with entropy weight and provided the entropy weighted water quality index (EWQI) for groundwater samples in Lenjanat plain, central Iran. The experimental results indicate that application of the EWQI is greatly helpful to identify and evaluate groundwater quality in Lenjanat, Iran. Singh^[10] systematically introduced the application of entropy theory in environmental and water engineering, and proposed the basic construction process of the evaluation model. Kholoosi et al^[11] used Entropy Based Water Quality Index (EBWQI) to assess groundwater quality and structured a new clustering method which was proposed based on multi objective optimization for EBWQIs data sets interpretation (MOC). The effectiveness of the MOC method was verified by comparing different clustering methods. Li et al^[12] proposed an improved TOPSIS-based approach called the Informative Weighting and Ranking (TIWR) method using the Criteria Importance Through Inter-criteria Correlation (CRITIC) approach, which avoids classifying several objects into the same typical level and makes them distinguishable.

TOPSIS model has been also widely applied in multiple other fields^[23-24], such as enterprise strength comparison^[25], safety of coal mines^[26], investment decision^[27], highway transportation^[28], urban sustainable development^[29-30], tourism competitiveness^[31], agricultural water resource management^[32], and so on. In the process of water quality assessment, uncertain and fuzzy factors are often encountered, so many researchers are enthusiastic about the research and application of entropy weight method based on fuzzy theory. Lots of researches have made considerable contributions to the fuzzy synthetic evaluation approaches with entropy method^[13-16], and applied fuzzy theory and TOPSIS method to water quality assessment based on entropy weight^[17-21]. An et al^[22] introduced a fuzzy rough set to perform attribute reduction, and combined an attribute recognition theoretical model and entropy method to assess water quality.

Above, we have introduced the extensive research work of scholars on water quality assessment based on the TOPSIS model. However, there are inevitably several problems in these works. First, subjective elements such as fuzzy theory or analytic hierarchy process (AHP) introduce human bias, potentially distorting results. Second, the method emphasizes the final evaluation matrix while neglecting the rich original sample data used to construct it, often relying on regional or annual averages that reduce accuracy. Moreover, traditional entropy-based weighting only considers statistical properties within the evaluation matrix, ignoring the more precise probability information available in the original data. Therefore, based on the framework provided by the above researches, this paper proposes a modified entropy weight approach with TOPSIS model to establish an improved comprehensive evaluation method. It is targeted for the situations that the composition values of evaluation matrix are derived from a large amount of data, such as the monthly multi-site wastewater monitoring data used in this paper. With the simultaneous consideration of the impact of subjective factors, this model evaluates the performances merely on the objective data.

The main structure of the paper is as follows: In Section 1, a modified method for entropy weight is introduced thoroughly and combined with TOPSIS to construct a rational and effective evaluation model. Section 2 provides some background information about the geographical characteristics of Guizhou Province, China, the acquisition of data sources and the establishment of evaluation criteria. In Section 3, a case study of water quality assessment in Guizhou Province, China, in terms of yearly and regional analysis is conducted to examine the applicability of the proposed model. Section 4 presents the conclusion.

1 TOPSIS Model with Modified Entropy Weight

1.1 The Entropy Weight Theory

1.1.1 Information entropy

Entropy theory first appeared in thermodynamics and was later introduced into information theory by Shannon^[33]. Subsequently, the concept of information entropy emerged as a measure of disorder degree and the amount of information conveyed by an event drawn from the probability distribution of a random event. In the probability distribution, the higher the probability of occurrence is, the smaller the uncertainty is and the less information it contains. Therefore, the average information provided by a random event can be quantified as follows:

$H(X)=-{\displaystyle \sum _{i=\mathrm{1}}^n}p(x_i)\mathrm{l}\mathrm{o}\mathrm{g}\left(p(x_i)\right)$

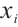where $x_i$ is the value of the random variable 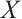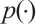$X$; $p(\cdot )$ is the probability of random event 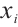$x_i$ occurring.

1.1.2 Modified entropy weight method

Information entropy can be used to measure the degree of differentiation of the indicator. The greater the dispersion degree of a indicator value, the greater the influence of the indicator on the comprehensive evaluation, and the higher weight should be given to the indicator. Differentiating from the traditional approach of processing weights in the entropy weight method, we make an improvement: Firstly, the approximate probability distribution of one indicator can be estimated from all measured value of this indicator; Secondly, the probability of every indicator value in evaluation objects can be obtained more precisely by locating it in the known probability distribution; Finally, with more accurate probabilities estimation, the accuracy of entropy calculation and the indicator weight improves, which adequately enhances the model performance. The specific implementation steps are as follows:

1) Assuming that there are 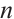$n$ measured values for 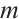$m$ previously defined indicator, and 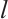$l$ assessment subjects, so the corresponding matrix can be expressed as:

$\mathit{X}=\left[\begin{array}{cccc}{x}_{\mathrm{11}}& x_{\mathrm{12}}& \cdots & x_{\mathrm{1}m}\\ x_{\mathrm{21}}& x_{\mathrm{22}}& \cdots & x_{\mathrm{2}m}\\ ⋮& ⋮& ⋮& ⋮\\ x_{n\mathrm{1}}& x_{n\mathrm{2}}& \cdots & x_{nm}\end{array}\right],\mathit{Y}=\left[\begin{array}{cccc}{y}_{\mathrm{11}}& y_{\mathrm{12}}& \cdots & y_{\mathrm{1}m}\\ y_{\mathrm{21}}& y_{\mathrm{22}}& \cdots & y_{\mathrm{2}m}\\ ⋮& ⋮& ⋮& ⋮\\ y_{l\mathrm{1}}& y_{l\mathrm{2}}& \cdots & y_{lm}\end{array}\right]$

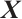where $\mathit{X}$ is the original sample data matrix, 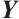$\mathit{Y}$ is the evaluation matrix, $l\ll n$.

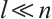2) To align data values to a common scale and distribution for comparison, normalization is applied to all acquired value 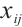$x_{ij}$ for each criterion. After the subtraction-based conversion procedure and frequency calculation in terms of 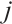$j$-th indicator, we proximate the probability distribution 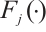$F_j(\cdot )$ for it by interpolating all handled data into cubic splines functions^[34-36]. The procedures are described as follows:

a) To unify indicator type, the subtraction-based conversion procedure is applied as follows:

For the benefit indicator: 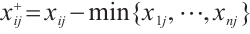$x_{ij}^{+}=x_{ij}-\mathrm{m}\mathrm{i}\mathrm{n}\{x_{\mathrm{1}j},\cdots ,x_{nj}\}$ ;

For the cost indicator: 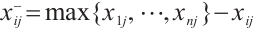$x_{ij}^{-}=\mathrm{m}\mathrm{a}\mathrm{x}\{x_{\mathrm{1}j},\cdots ,x_{nj}\}-x_{ij}$ ;

For the interval indicator:

$x_{ij}^{-}=\mathrm{m}\mathrm{a}\mathrm{x}\{\left|x_{\mathrm{1}j}-{\widehat{x}}_j\right|,\cdots ,\left|x_{nj}-{\widehat{x}}_j\right|\}-\left|x_{ij}-{\widehat{x}}_j\right|$

b) Build a frequency table 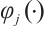${\phi }_j(\cdot )$ for each converted indicator value 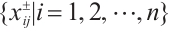$\{x_{ij}^{\pm }|i=\mathrm{1,2},\cdots ,n\}$ and transform it into 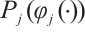$P_j({\phi }_j(\cdot ))$ which is the approximate probability of 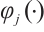${\phi }_j(\cdot )$ with being obtained by using the frequency 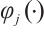${\phi }_j(\cdot )$ divided by the total number of values.

c) Proximate the probability distribution 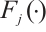$F_j(\cdot )$ by fitting 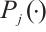$P_j(\cdot )$ with cubic spline interpolation method as follows:

$F_j(x_{ij}^{\pm })=$

$\{\begin{array}{l}\mathrm{S}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}(P_j({\phi }_j(x_{ij}^{\pm }))),\\ \mathrm{i}\mathrm{f}\mathrm{S}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}(P_j({\phi }_j(x_{ij}^{\pm })))\in [\mathrm{0},\mathrm{m}\mathrm{a}\mathrm{x}\{P_j({\phi }_j(x_j^h))\}];\\ \frac{P_j({\phi }_j(x_j^h))+P_j({\phi }_j(x_j^{h+\mathrm{1}}))}{\mathrm{2}},\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{s};\end{array}$(1)

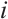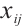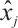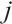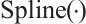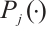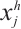where $i$ is the sample data number index, $j$ is the indicator index, $x_{ij}$ is the corresponding value located in the sample data, ${\widehat{x}}_j$ is the ideal value of the $j$-th indicator, $\mathrm{S}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}(\cdot )$ is the cubic spline interpolation function of $P_j(\cdot )$, and $x_j^h$ is the data point of ${\phi }_j(\cdot )$, $x_{ij}^{\pm }\in [x_j^h,x_j^{h+\mathrm{1}})$.

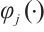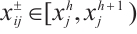3) Calculate the entropy of each dimension of assessment subject 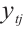$y_{tj}$ based on the probability distribution of each indicator. Its expressions are shown as follows:

$E_j=-\frac{\mathrm{1}}{\mathrm{l}\mathrm{n}l}{\displaystyle \sum _{t=\mathrm{1}}^l}{p}_{tj}\mathrm{l}\mathrm{n}\left(p_{tj}\right)$

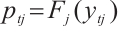where $p_{tj}=F_j(y_{tj})$ is the probability of 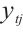$y_{tj}$ by (1), $t=\mathrm{1,2},\cdots ,l$.

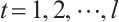4) The weight of 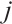$j$-th evaluation indicator is expressed as follows:

$w_j=\frac{\mathrm{1}-E_j}{m-\sum _j{E}_j},j=\mathrm{1,2},\cdots ,m.$(2)

1.2 The Methodology of TOPSIS

TOPSIS is a multiple objective decision making method which was firstly proposed by Hwang and Yoon in 1981^[37], and Yoon made some further researches in 1995^[38]. TOPSIS, which uses the comparison between the distance of the solution from the positive ideal solution and the distance of the solution from negative ideal solution, determines the priority order of the assessed subjects. Positive ideal solution is defined as the composition of all the best value achieved for each indicator, while negative ideal solution contains all the worst value. The evaluation procedures of TOPSIS method are as follows:

1) Calculate the weighted normalized decision matrix

$Z={\left(z_{tj}\right)}_{l\times m}=\left(p_{tj}\times w_j\right)$

2) Determine the positive ideal solution 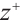$z^{+}$ and the negative solution $z^{-}$:

$\{\begin{array}{l}{z}^{+}=\left\{z_j^{+}\right\}=\left\{\mathrm{m}\mathrm{a}\mathrm{x}\left\{z_{\mathrm{1}j},z_{\mathrm{2}j},\cdots ,z_{lj}\right\}|j=\mathrm{1,2},\cdots ,m\right\}\\ z^{-}=\left\{z_j^{-}\right\}=\left\{\mathrm{m}\mathrm{i}\mathrm{n}\left\{z_{\mathrm{1}j},z_{\mathrm{2}j},\cdots ,z_{lj}\right\}|j=\mathrm{1,2},\cdots ,m\right\}\end{array}$(3)

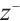3)　Calculate the Euclidean distance of each assessment subject to positive ideal solution 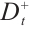${\mathit{D}}_{\mathit{t}}^{+}$ and negative ideal solution ${\mathit{D}}_{\mathit{t}}^{-}$:

$\{\begin{array}{c}{D}_t^{+}=\sqrt[]{{\displaystyle \sum _{j=\mathrm{1}}^m}{\left(z_{tj}-z_j^{+}\right)}^{\mathrm{2}}}\\ D_t^{-}=\sqrt[]{{\displaystyle \sum _{j=\mathrm{1}}^m}{\left(z_{tj}-z_j^{-}\right)}^{\mathrm{2}}}\end{array}$(4)

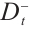4) Calculate the similarity of each assessment subject 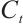$C_t$ to the worst condition, and obtain the corresponding grade in centesimal grade system. The higher the grade, the better the evaluation result of this alternative subject.

$C_t=\frac{\mathrm{100}{D}_t^{-}}{D_t^{+}+D_t^{-}},t=\mathrm{1,2},\cdots ,l.$(5)

1.3 TOPSIS with Modified Entropy Weight

Based on the concept and methodology mentioned in Sections 1.1 and 1.2, the application steps (evaluation procedure) for the TOPSIS model with our modified entropy weights (as MEW-TOPSIS below) can be briefed as follows:

Step 0.   Normalize data and calculate approximate probability distribution 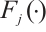$F_j(\cdot )$ by Eq. (1).

Step 1.   Determine the weight of j-th indicator by Eq. (2).

Step 2.   Calculate the distance of each assessed subject to the positive ideal solution 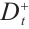$D_t^{+}$ and the negative ideal solution 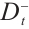$D_t^{-}$ by Eq. (4).

Step 3.   Sort the grade of assessment subjects from smallest to largest by Eq. (5).

1.4 Rank Correlation Knowledge

In statistics, the two commonly-used measures of statistical dependence between two ranked variable are Spearman^[39] and Kendall^[40] rank correlation coefficient. In Section 3, to examine the effectiveness and superiority of the proposed model, these two coefficients are set as the performance indicators for different evaluation methods. The calculation formulas for these two coefficients are expressed as follows: Spearman rank correlation coefficient is given by

$\rho =\mathrm{1}-\frac{\mathrm{6}\sum d_i^{\mathrm{2}}}{n(n^{\mathrm{2}}-\mathrm{1})},$(6)

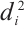where $d_i^{\mathrm{2}}$ is the difference between paired ranks, n is the number of paired items, $\rho \in [-\mathrm{1,1}]$.

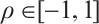Kendall rank correlation coefficient is given by

$\tau =\frac{\mathrm{4}p}{n(n-\mathrm{1})}-\mathrm{1},$(7)

where p is the number of pairs items in the same order, 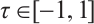$\tau \in [-\mathrm{1,1}]$.

2 Supplementary Information

2.1 Geological Information

Guizhou Province is located in the Yunnan-Guizhou Plateau of China, between 103°36′E - 109°35′E and 24°37′N - 29°13′N. As of 2021, the total area of the province is 176 200 km², accounting for 1.8% of the national total area. With 6 prefecture level cities and 3 autonomous prefectures, the province has a permanent population of 38.52 million people.

There are many rivers in Guizhou Province, and there are 984 rivers with length over 10 km, such as Wujiang River, Chishui River, Qingshui River, Nanpanjiang River, Beipanjiang River and Hongshui River, etc. In 2021, the river runoff in Guizhou Province reaches 105.3 billion cubic meters. The mountainous features of Guizhou's rivers are obvious. Most of the upstream rivers have open valleys with gentle water flow and little water volume; the midstream rivers have interlocking valleys with rapid water flow; the downstream rivers have deep and narrow valleys with large water volume and rich hydraulic resources.

2.2 Data Acquisition

The sample data used in this paper is the site-specific estimates of contaminant exposure (mainly concentration or concentration statistics) acquired from the wastewater monitoring system of large-scale companies in Guizhou Province, and is published by the Department of Ecology and Environment of Guizhou Province on its official website. By focusing on the water quality within recent years, the data in the period from 2018 to 2022 is selected. The number of data resource are represented in Fig. 1. We can know from Fig. 1(b) that Guiyang City, as the capital city of Guizhou Province, has a total number of 4 100 data values acquired from 2018 to 2022 with ranking first among 9 prefecture-level divisions.

Fig. 1 Number of related data resource

2.3 Evaluation Criteria

The Ministry of Ecology and Environment of the People's Republic of China promulgated the China Surface Water Environmental Quality Standard (GB3838-2002) in 2002, listing 24 representative indicators and the national-scale benchmarks for screening-level assessment of surface water environmental quality. However, considering the difficulty of data access and the scarcity of sample data on some attributes, 18 indicators were chosen for the assessment criteria and presented in Table 1 with the corresponding threshold values and levels of water quality.

3 Result and Discussion

In this section, we apply the proposed model for yearly evaluation water quality across the regions in Guizhou Province with the dataset and criteria mentioned in Sections 2.2 and 2.3. As the implementation procedure stated in Section 1, estimated probability distribution for each criterion is fitted by all sample data of it, presented as a separated graph in Fig. 2. From the visualization of probability distributions, we can figure out that the fitted probability distributions are generally in line with the actual situation, except for some points in Fig. 2(j) that deviate slightly.

Fig. 2 Cubic spline interpolation of probability distribution 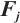${\mathit{F}}_{\mathit{j}}$

In order to scientifically and comprehensively demonstrate the overall changes of water environment in Guizhou Province, the comparative analysis is conducted from two aspects. On the one hand, to see the trend over time, our evaluation is based on the yearly average value of each criterion from 2018 to 2022; On the other hand, in a comprehensive water quality evaluation, the regional comparative analysis should be concerned, so an analysis based on the yearly average of each criterion of every prefecture-level division from 2018 to 2022 has been run.

3.1 Annual Analysis (2018-2022)

The yearly average values of predetermined indicator from 2018 to 2022 are shown in Table 2. The evaluation matrix 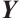$\mathit{Y}$ in our model is composed of each of them.

To prove the effectiveness and superiority of the methodology proposed in this paper, we selected the other two approaches to run comparative analysis as follows:

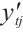a) TEW: Use traditional entropy weight methodology for calculating weights, where $p_{tj}=\frac{y_{tj}^{\text{'}}}{{\displaystyle \sum _{t=\mathrm{1}}^l}{y}_{tj}^{\text{'}}}$ and $y_{tj}^{\text{'}}$ has been normalized by Max-Minimum regularization method;

b) Wei(x): Use the methodology proposed by Chiang et al^[41] to calculate the entropy weight, where

$E_j=\frac{\mathrm{1}}{\mathrm{0.6487}l}{\displaystyle \sum _{t=\mathrm{1}}^l}\mathrm{W}\mathrm{e}\mathrm{i}\left(\frac{y_{tj}^{\text{'}}}{{\displaystyle \sum _{t=\mathrm{1}}^l}{y}_{tj}^{\text{'}}}\right)$

$\mathrm{W}\mathrm{e}\mathrm{i}(x)=x{\mathrm{e}}^{(\mathrm{1}-x)}+(\mathrm{1}-x){\mathrm{e}}^x-\mathrm{1},j=\mathrm{1,2},\cdots ,m$

c) MEW: Use the modified entropy weight methodology proposed in this paper (see Section 1.3).

Baijiu (a special Chinese liquor) industry is known as one of the pillar industries and has been the mainly driving force of economic growth in Guizhou Province. It is logical to infer that there exists a direct relationship between the output of Baijiu and the quality of water environment because the volume of industrial sewage discharged will inevitably increases once the production volume of Baijiu increases. Therefore, the evaluation model performance can be measured by the correlation between the annual output of Baijiu and the yearly grade got from model. For this, Spearman and Kendall rank correlation coefficients are selected as the reasonable indicators of model performance (see Section 1.4). Moreover, the data related to Baijiu we used is the annual output of Baijiu enterprises above designated size in 2018-2022 published by National Bureau of Statistics. The related results are shown in Table 3.

Both rank correlation coefficients show that there is a negative correlation between Baijiu production and water quality. This is consistent with the inference mentioned above. Furthermore, these two rank correlation coefficients, which are also indicators of model performance, turn out to be closer to -1 while calculating the correlation between the evaluation result obtained from our proposed model and annual output of Baijiu, sufficiently justifing that it is a more favorable approach than the other two. Additionally, it is noticeable that the annual output of Baijiu in 2020 was the lowest. Part of the reason for this is the outbreak of the COVID-19 epidemic. There were severe disruptions on economy and society triggered by this, including decreased social mobility, slow-down in all industry production and so on. Reduced human activity led to predictable decrease in pollution, so that the volume of sewage discharged hit the bottom in this year, and water environment improved significantly at same time, which is precisely consistent with the rank-order of the evaluation grade in 2020 got by our proposed model.

3.2 Regional Analysis

There are nine prefecture-level divisions in Guizhou Province, including Guiyang, Zunyi, Bijie, Liupanshui, Qiandongnan, Qianxinan, Qiannan, Tongren and Anshun. The evaluation from a regional perspective is beneficial to understand the detailed changes in the water environment of Guizhou Province, and build a dynamic pollution map based on the inter-regional comparison with the time trend basically. Similarly, we use the novel methodology MEW-TOPSIS to evaluate the water quality of these nine regions on an annual basis (see Table 4).

The evaluation results show that the water quality of most cities in Guizhou Province has decreased to varying degrees in the past two years, except for Zunyi and Bijie which have a significant improvement in water quality. As the political, economic, cultural, educational, scientific and technological center of Guizhou Province, Guiyang has maintained a high social mobility and orderly production operations for three years since the COVID-19 epidemic, and the water quality has slightly declined. After the epidemic, the resumption of work and production will be promoted in a sequential manner. In this process, it is even more important to strengthen the protection of the water environment, strictly control the discharge of sewage, and improve the environmental protection awareness of production enterprises. In addition, the water environment in the three southern autonomous prefectures of Guizhou Province has also deteriorated, which requires high attention from local departments.

4 Conclusion

With the subtle improvement in entropy weight methodology, the modified model we proposed exploits the useful information of data to a maximum extent. The improvement is specified as using cubic spline interpolation to fit a more proper and accurate probability distribution for each indicator in evaluation and substituting the original way of probability calculation for the entropy weight method with it. Then, an improved comprehensive evaluation model for water quality is constructed scrupulously by combining it with the TOPSIS model. To prove its practicality and superiority, a case study of water quality assessment of Guizhou Province was conducted by using the wastewater monitoring data of large-scale companies, and two rank correlation coefficients are set as model performance indicators on the foundation of a solid inference about the relationship between the production Baijiu and water environment. In final, the outcomes not only suggest the boosted effectiveness and accuracy of model but also projects a simplified panorama of water quality changes of Guizhou Province in recent five years, which contributes to remind some local authorities specially the ones in Bijie and Zunyi city to pay more attention to the water environment and enforce pollution control at sources. In addition to be applied on water quality assessment, the high flexibility and versatility of the model we proposed is expected to accommodate further extensions and be put into practice in various fields.

References

All Tables

All Figures

	Fig. 1 Number of related data resource
In the text

	Fig. 2 Cubic spline interpolation of probability distribution 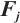${\mathit{F}}_{\mathit{j}}$
In the text