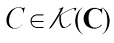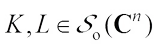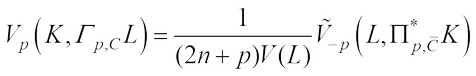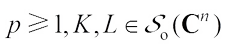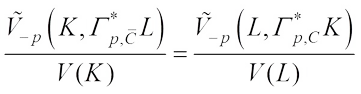| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 27, Number 1, March 2022
|
|
|---|---|---|
| Page(s) | 42 - 48 | |
| DOI | https://doi.org/10.1051/wujns/2022271042 | |
| Published online | 16 March 2022 | |
Mathematics
CLC number: O18
Inequalities on Complex Lp Centroid Bodies
College of Science & Three Gorges Mathematical Research Center, China Three Gorges University, Yichang 443002, Hubei, China
† To whom correspondence should be addressed. E-mail: zhyp5208@163.com
Received: 25 September 2021
Based on the notion of the complex Lp centroid body, we establish Brunn-Minkowski type inequalities and monotonicity inequalities for complex Lp centroid bodies in this article. Moreover, we obtain the affirmative form of Shephard type problem for the complex Lp centroid bodies and its negative form.
Key words: complex Lp centroid body / Brunn-Minkowski type inequalities / Shephard type problem
Biography: CHENG Manli, female, Master candidate, research direction: convex geometric analysis. E-mail: 1806857113@qq.com
Foundation item: Supported by the National Natural Science Foundation of China (11901346)
© Wuhan University 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Let 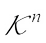 denote the set of convex bodies (compact, convex sets with non-empty interiors) in Euclidean space
denote the set of convex bodies (compact, convex sets with non-empty interiors) in Euclidean space 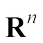 . For the set of convex bodies containing the origin in their interiors, the set of origin-symmetric convex bodies, we write
. For the set of convex bodies containing the origin in their interiors, the set of origin-symmetric convex bodies, we write 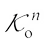 and
and 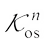 , respectively. Let V(K) denote the volume of K and
, respectively. Let V(K) denote the volume of K and  the unit sphere.
the unit sphere.
Centroid bodies are a classical notion from geometry which have attracted increasing attention in recent years[1-11]. In 1997, Lutwak and Zhang [12] introduced the concept of 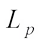 centroid body as follows: For each compact star-shaped about the origin
centroid body as follows: For each compact star-shaped about the origin  and
and 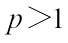 , the
, the 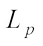 centroid body,
centroid body, 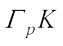 , of K is the origin-symmetric convex body whose support function is defined by
, of K is the origin-symmetric convex body whose support function is defined by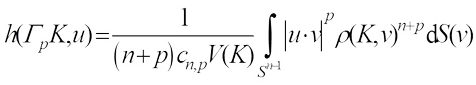 (1)for any
(1)for any  . Refs. [13-19] had conducted a series of studies on the
. Refs. [13-19] had conducted a series of studies on the 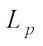 centroid body, and many scholars were attracted. The
centroid body, and many scholars were attracted. The 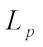 centroid body has got many results from these articles. Particularly, Refs. [20, 21] gave the Brunn-Minkowski inequality and monotonicity inequality for the
centroid body has got many results from these articles. Particularly, Refs. [20, 21] gave the Brunn-Minkowski inequality and monotonicity inequality for the 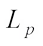 centroid body. Grinberg and Zhang [22] gave the Shephard problems for the
centroid body. Grinberg and Zhang [22] gave the Shephard problems for the 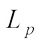 centroid body.
centroid body.
However, complex convex geometry has been studied in many works[23-28]. In this paper, we mainly study the complex centroid body. First, we introduce some notations in complex vector space 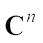 . Let
. Let 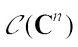 denote the set of compact convex subsets of complex vector space
denote the set of compact convex subsets of complex vector space 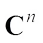 . Let
. Let  ,
, 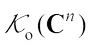 and
and 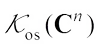 denote the set of complex convex bodies, the set of complex convex bodies containing the origin in their interiors, and the set of origin symmetric complex convex bodies, respectively. Let
denote the set of complex convex bodies, the set of complex convex bodies containing the origin in their interiors, and the set of origin symmetric complex convex bodies, respectively. Let  ,
, 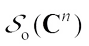 and
and 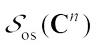 denote the set of complex star bodies, the set of complex star bodies containing the origin in their interiors, and the set of origin symmetric complex star bodies, respectively.
denote the set of complex star bodies, the set of complex star bodies containing the origin in their interiors, and the set of origin symmetric complex star bodies, respectively.  stands for the complex unit sphere.
stands for the complex unit sphere.
Harberl[29] firstly proposed the complex centroid body of K and established the Busemann-Petty centroid inequality. In 2021, Wu[30] introduced the concept of the 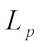 complex centroid body
complex centroid body 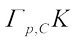 as follows: If
as follows: If 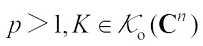 and
and  , the complex
, the complex 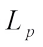 centroid body
centroid body 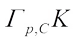 is the convex body with support function
is the convex body with support function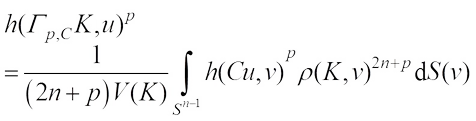 (2)where the integration is with respect to the push forward of the Lebesgue measure under the canonical isomorphism
(2)where the integration is with respect to the push forward of the Lebesgue measure under the canonical isomorphism 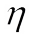 and as for
and as for 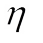 , it is the canonical isomorphism between
, it is the canonical isomorphism between 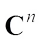 and
and 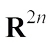 , i.e.,
, i.e.,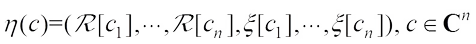 where
where  are the real part and imaginary part, respectively. It is obvious to get that if
are the real part and imaginary part, respectively. It is obvious to get that if 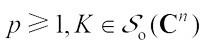 , then
, then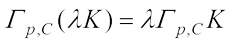 (3)
(3)
In this article, associated with the definition of complex 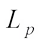 centroid body, we continuously study the complex
centroid body, we continuously study the complex 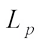 centroid body. Let
centroid body. Let 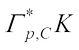 denote the polar of
denote the polar of 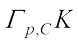 and
and 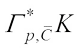 denote the polar for complex conjugate of
denote the polar for complex conjugate of 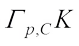 . First, we establish the Brunn-Minkowski type inequalities for complex
. First, we establish the Brunn-Minkowski type inequalities for complex 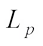 centroid bodies.
centroid bodies.
Theorem 1 If 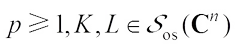 and
and 
 , then
, then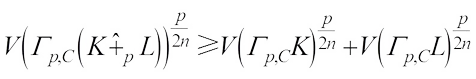 (4)with equality if and only if K and L are real dilation.
(4)with equality if and only if K and L are real dilation.
Theorem 2 If 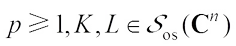 and
and 
 , then
, then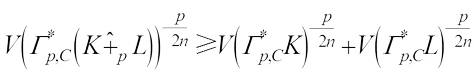 (5)with equality if and only if L and K are real dilation.
(5)with equality if and only if L and K are real dilation.
Then we obtain monotonicity inequalities for complex 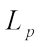 centroid bodies.
centroid bodies.
Theorem 3 For 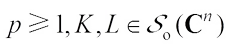 ,
, 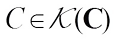 , if
, if 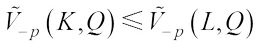 for any
for any 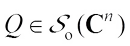 , then
, then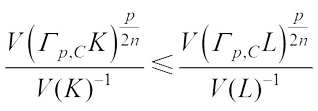 (6)with equality if and only if K=L.
(6)with equality if and only if K=L.
Theorem 4 For 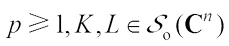 ,
, 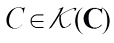 , if
, if 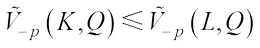 , for any
, for any 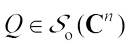 , then
, then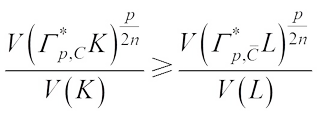 (7)with equality if and only if K=L.
(7)with equality if and only if K=L.
Finally, we study the 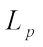 Shephard type problem of complex
Shephard type problem of complex 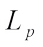 centroid bodies and give the negative form.
centroid bodies and give the negative form.
Theorem 5 Let 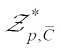 denote the set of polar for complex conjugate of
denote the set of polar for complex conjugate of 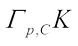 . For
. For 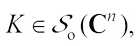
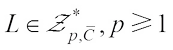 , if
, if 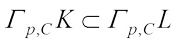 , then
, then 
 with equality if and only if K=L.
with equality if and only if K=L.
Theorem 6 For 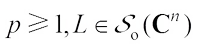 , if L is not origin symmetric star body, then there exists
, if L is not origin symmetric star body, then there exists 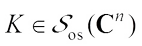 such that
such that 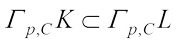 , but
, but 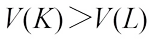 .
.
Throughout this paper, we assume that  .
.
1 Preliminaries
In this section, we collect complex reformulations of well-known results from convex geometry. These complex versions can be directly deduced from their real counterparts by an appropriate application of  . For standard reference, the readers may consult the books of Gardner[31] and Schneider[32].
. For standard reference, the readers may consult the books of Gardner[31] and Schneider[32].
1.1 Complex Support Functions and Radial Functions
For a complex number  , we write
, we write 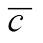 for its conjugate and |c| for its norm. If
for its conjugate and |c| for its norm. If  , then
, then 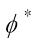 denotes the conjugate transpose of
denotes the conjugate transpose of 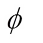 and if
and if 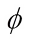 is invertible,
is invertible, 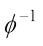 denotes the inverse of
denotes the inverse of 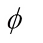 . A complex convex body
. A complex convex body 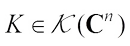 is uniquely determined by its support function
is uniquely determined by its support function 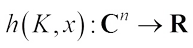 ,
,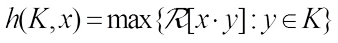 where “∙” means the standard Hermitian inner production in
where “∙” means the standard Hermitian inner production in 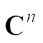 and
and 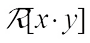 is the real part of
is the real part of 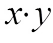 . It is easy to see that
. It is easy to see that 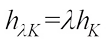 for all
for all 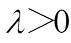 and
and 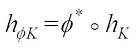 for all
for all  . The complex radial function
. The complex radial function 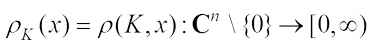 of a compact star- shaped (about the origin)
of a compact star- shaped (about the origin)  is defined, for x∈Cn\{0}, by
is defined, for x∈Cn\{0}, by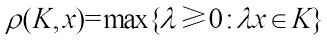 It is easy to see that
It is easy to see that 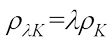 for all
for all 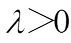 and
and 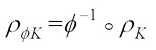 for all
for all  . If
. If 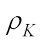 is positive and continuous, K will be called a star body. Moreover, if
is positive and continuous, K will be called a star body. Moreover, if  , it is easy to certify that
, it is easy to certify that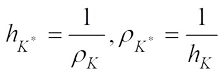 (8)
(8)
An application of polar coordinates to the volume of a complex star body 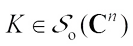 gives that
gives that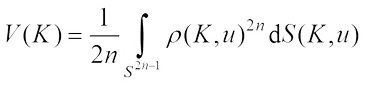
1.2 Complex Lp Mixed Volume and Dual Lp Mixed Volume
For 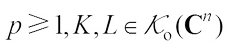 and
and 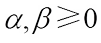 (not both zero), the complex
(not both zero), the complex 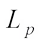 Minkowski combination
Minkowski combination  is defined by
is defined by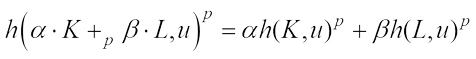 The complex
The complex 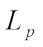 mixed volume,
mixed volume, 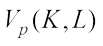 of
of 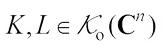 is defined by (see Ref.[33])
is defined by (see Ref.[33])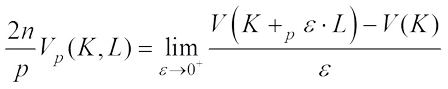 (9)By (9) we have
(9)By (9) we have 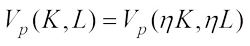 and for
and for  ,
,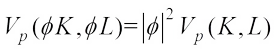 For every Borel set
For every Borel set 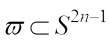 , the complex surface area measure
, the complex surface area measure 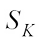 of
of 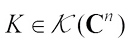 is defined by
is defined by where
where 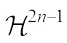 stands for (2n-1)-dimensional Hausdorff measure on
stands for (2n-1)-dimensional Hausdorff measure on  .
.
In addition, the complex surface area measures are translation invariant and 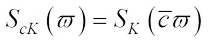 for all
for all  and each Borel set
and each Borel set 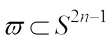 . If
. If 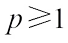 , we define the complex
, we define the complex 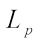 surface area measure
surface area measure 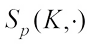 of
of 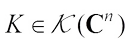 as
as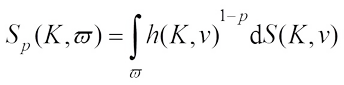 For
For 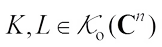 , there is the
, there is the 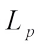 surface area measure
surface area measure 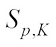 of K on
of K on  such that
such that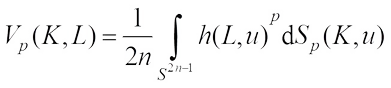 (10)It turns out that the measure
(10)It turns out that the measure 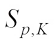 is absolutely continuous with respect to
is absolutely continuous with respect to 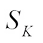 and has Radon Nikodym derivative
and has Radon Nikodym derivative 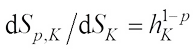 . There is the complex
. There is the complex 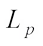 Minkowski inequality for complex convex body: If
Minkowski inequality for complex convex body: If 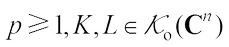 , then
, then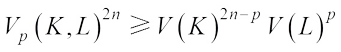 (11)with equality if and only if K and L are real dilation. The real
(11)with equality if and only if K and L are real dilation. The real 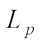 Minkowski inequality and its proof are shown in Ref . [32] .
Minkowski inequality and its proof are shown in Ref . [32] .
For 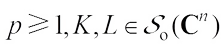 and
and 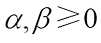 (not both zero), the complex
(not both zero), the complex 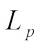 harmonic radial combination
harmonic radial combination 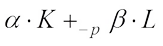 is defined by
is defined by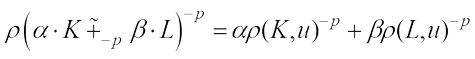 Then the dual complex
Then the dual complex 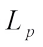 mixed volume
mixed volume 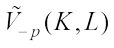 is defined by (see Ref.[33])
is defined by (see Ref.[33])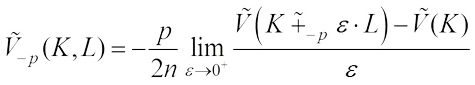 The polar coordinate formula for volume yields
The polar coordinate formula for volume yields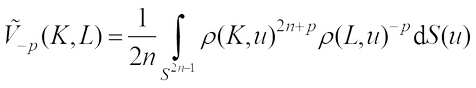 (12)Particularly,
(12)Particularly, 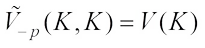 .
.
The integral representation (12), together with the Hӧlder inequality[34] immediately gives that (13)with equality if and only if K and L are real dilation. For the real
(13)with equality if and only if K and L are real dilation. For the real 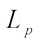 harmonic radial combination and real
harmonic radial combination and real 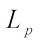 dual Minkowski inequality, we refer to Ref. [35].
dual Minkowski inequality, we refer to Ref. [35].
1.3 The Complex Lp Harmonic Blaschke Combination
The notion of real 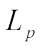 harmonic Blaschke combination was given by Lu and Leng[36]. Then, we extend real
harmonic Blaschke combination was given by Lu and Leng[36]. Then, we extend real 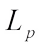 harmonic Blaschke combination to the complex case.
harmonic Blaschke combination to the complex case.
For 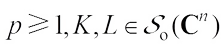 and
and 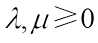 (not both zero), the complex
(not both zero), the complex 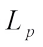 harmonic Blaschke combination
harmonic Blaschke combination 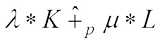 of K and L is defined by
of K and L is defined by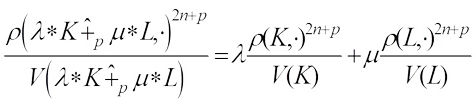 (14)where
(14)where  is
is 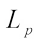 harmonic Blaschke scalar multiplication and
harmonic Blaschke scalar multiplication and 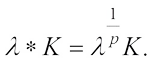 Taking
Taking 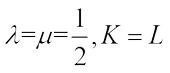 in
in 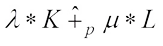 , then the complex
, then the complex 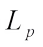 harmonic Blaschke body
harmonic Blaschke body 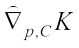 is introduced by
is introduced by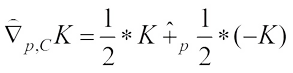 (15)Obviously,
(15)Obviously, 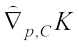 is origin symmetric.
is origin symmetric.
2 Proofs of Theorems
In this section, we will prove Theorem 1-Theorem 6.
Proof of Theorem 1 For 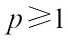 and
and 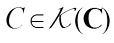 , the
, the 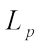 harmonic Blaschke combination (14) together with (2) yields
harmonic Blaschke combination (14) together with (2) yields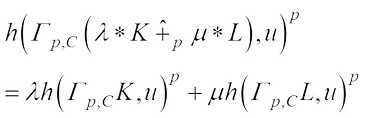 (16)
(16)
From (10) and for any 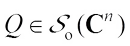 , we obtain
, we obtain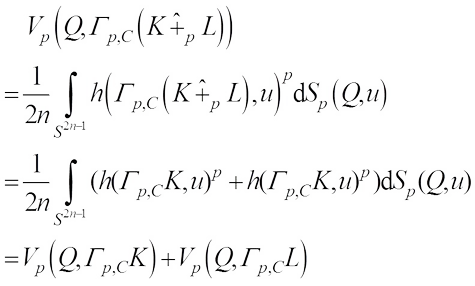 Therefore, by (11), we get
Therefore, by (11), we get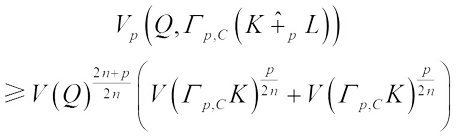 (17)with equality if and only if
(17)with equality if and only if 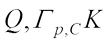 and
and 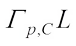 are real dilation. Taking
are real dilation. Taking 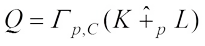 in (17), one has
in (17), one has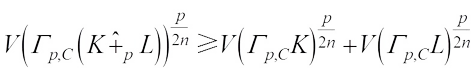 Together (16) with the equality condition of (17), we know that the equality holds if and only if K and L are real dilation.
Together (16) with the equality condition of (17), we know that the equality holds if and only if K and L are real dilation.
Proof of Theorem 2 From (8) and (16), one has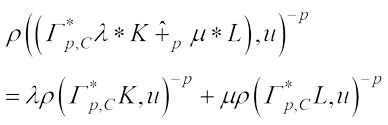 (18)
(18)
Then by (12) and the inverse Minkowski’s integral inequality[34], we obtain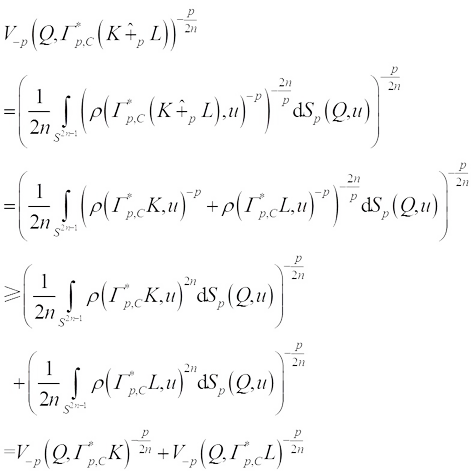 (19)Taking
(19)Taking 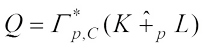 in (19) and by (13), one yields the inequality (6). According to the equality conditions of Minkowski’s integral inequalities, we see that equality holds in (19) if and only if K and L are real dilation.
in (19) and by (13), one yields the inequality (6). According to the equality conditions of Minkowski’s integral inequalities, we see that equality holds in (19) if and only if K and L are real dilation.
Next, we turn to prove Theorem 3 and Theorem 4. Lemma 1 provides a connection of 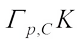 and
and 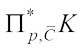 in terms of mixed volumes and their dual.
in terms of mixed volumes and their dual.
Proof From (3), (8), (10) and definition of 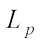 projection body[29], we have
projection body[29], we have which ends the proof of Lemma 1.
which ends the proof of Lemma 1.
Proof From (3), (8) and (12), it easily gets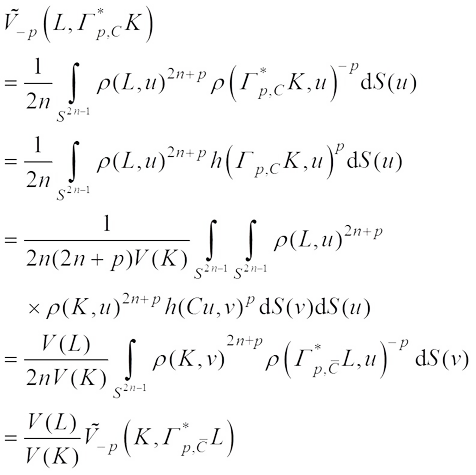 That is to say,
That is to say,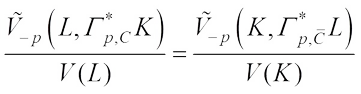 which yields (21).
which yields (21).
Remark 1 If 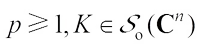 , then
, then 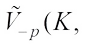
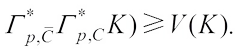 If K is a central ellipsoid or an Hermitian ellipsoid, then the equality holds.
If K is a central ellipsoid or an Hermitian ellipsoid, then the equality holds.
Now we are in a position to prove Theorem 3 and Theorem 4.
Proof of Theorem 3 Since 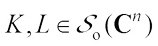 and
and  for any
for any 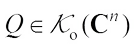 , then taking
, then taking 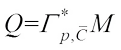 for any
for any 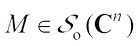 , we have
, we have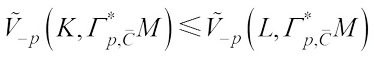 (22)with equality if and only if K = L. By Lemma 1, we obtain
(22)with equality if and only if K = L. By Lemma 1, we obtain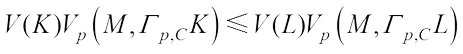 (23)
(23)
Taking 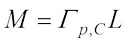 in (23) and by (11), one has
in (23) and by (11), one has (24)with equality in the second inequality of (24) if and only if
(24)with equality in the second inequality of (24) if and only if 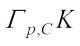 and
and 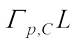 are real dilation. Thus, it follows from (24) that we have
are real dilation. Thus, it follows from (24) that we have i.e.,
i.e.,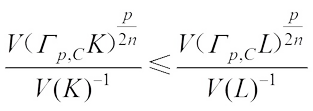 (25)
(25)
From Lemma 1, we see that inequalities (22) and (23) are equivalent. Thus, equality holds in (25) if and only if K = L.
Proof of Theorem 4 Since 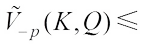
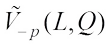 for any
for any 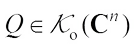 , then, taking
, then, taking 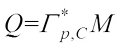 for any
for any 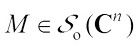 , we get
, we get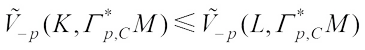 (26)with equality if and only if K = L. Combining (21) and (26), we obtain
(26)with equality if and only if K = L. Combining (21) and (26), we obtain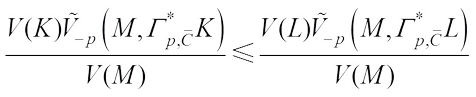 (27)Taking
(27)Taking 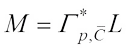 and by (13), it yields
and by (13), it yields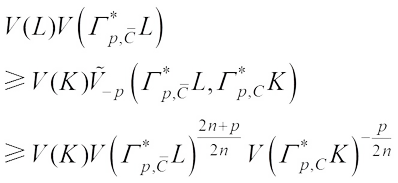 (28)with equality in the second inequality of (30) if and only if
(28)with equality in the second inequality of (30) if and only if 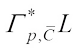 and
and 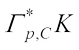 are real dilation. Thus, it follows from (28) that we have
are real dilation. Thus, it follows from (28) that we have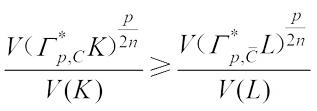 (29)with equality if and only if K = L.
(29)with equality if and only if K = L.
Now, we are dedicated to proving Theorem 5 and Theorem 6.
Proof of Theorem 5 For 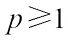 and
and 
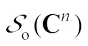 , it follows from the Lemma 2,
, it follows from the Lemma 2,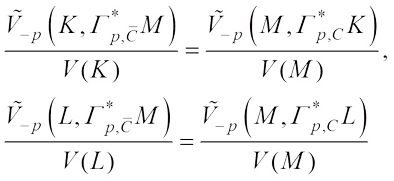 (30)Since
(30)Since 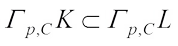 , then
, then 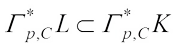 , hence for all
, hence for all 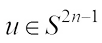 , we have
, we have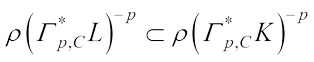 (31)Combining (30) and (31), we get
(31)Combining (30) and (31), we get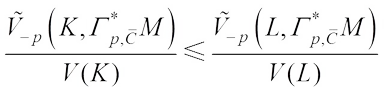 (32)For
(32)For 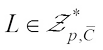 and taking
and taking 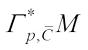 for L in (32), then from (13), we get
for L in (32), then from (13), we get  with equality if and only if K = L.
with equality if and only if K = L.
Proof of Theorem 6 By (3), (15) and (16), we have (33)Meanwhile, according to (12), (13) and (14), it yields
(33)Meanwhile, according to (12), (13) and (14), it yields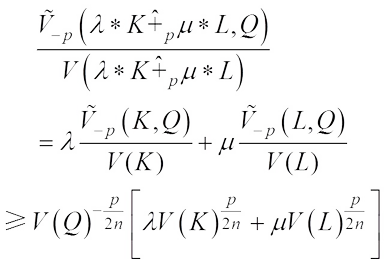 (34)Taking
(34)Taking  and
and 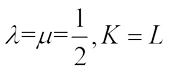 in (34), then
in (34), then 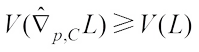 with equality if and only if L is an origin symmetric body.
with equality if and only if L is an origin symmetric body.
Since L is not an origin symmetric, we get 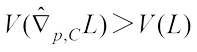 . Choose
. Choose  such that
such that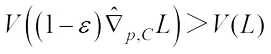
Let 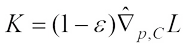 , then
, then 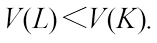 According to (3), we see that
According to (3), we see that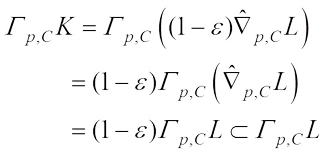 which ends the proof of Theorem 6.
which ends the proof of Theorem 6.
References
- Bernig A. Centroid bodies and the convexity of area functionals [J]. The Journal of Differential Geometry, 2014, 98(3): 357-373. [Google Scholar]
- Chen F, Yang C. A new proof of the Orlicz-Lorentz centroid inequality [J]. Journal of Inequalities and Applications, 2019, 2019(1): 1-12. [CrossRef] [PubMed] [Google Scholar]
- Lutwak E. On some affine isoperimetric inequalities [J]. The Journal of Differential Geometry, 1986, 23(1):1-13. [Google Scholar]
- Lutwak E. Centroid bodies and dual mixed volumes [J]. Proceedings of the London Mathematical Society, 1990, 60(2): 365-391. [CrossRef] [Google Scholar]
- Lutwak E, Yang D, Zhang G Y. The Cramer-Rao inequality for star bodies [J]. Duke Mathematical Journal, 2002, 112(1): 59-81. [MathSciNet] [Google Scholar]
- Lutwak E, Yang D, Zhang G Y. Orlicz centroid bodies [J]. The Journal of Differential Geometry, 2010, 84(2): 365-387. [Google Scholar]
- Petty C M. Centroid surfaces [J]. Pacific Journal of Mathematics, 1961, 11(3):1535-1547. [CrossRef] [MathSciNet] [Google Scholar]
- Shi K J, Wang Y. The asymmetric version of generalized centroid bodies [J]. Communication on Applied Mathematics and Computation, 2018, 32(3): 425-436. [MathSciNet] [Google Scholar]
- Xiong G, Xu D. Orlicz centroid bodies of ellipsoids [J]. Communication on Applied Mathematics & Computation, 2012, 26(1): 365-388. [Google Scholar]
- Yu W Y, Wu D H. The monotony properties of generalized projection bodies, intersection bodies and centroid bodies [J]. Journal of the Korean Mathematical Society, 2006, 43: 609-622. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Zhu G X. The Orlicz centroid inequality for star bodies [J]. Advances in Applied Mathematics, 2012, 48(2): 432-445. [CrossRef] [MathSciNet] [Google Scholar]
- Lutwak E, Zhang G Y. Blaschke-Santalӧ inequalities [J]. The Journal of Differential Geometry, 1997, 47(1): 1-16. [Google Scholar]
- Feng Y B, Wang W D. The Shephard type problems and monotonicity for Lp-mixed centroid bodies [J]. Indian Journal of Pure & Applied Mathematics, 2014, 45(3): 265-284. [CrossRef] [MathSciNet] [Google Scholar]
- Feng Y B, Wang W D. Shephard type problems for Lp centroid bodies [J]. Mathematical Inequalities & Applications, 2014, 17(3): 865-877. [MathSciNet] [Google Scholar]
- Feng Y B, Wang W D, Lu F H. Some inequalities on general Lp centroid bodies [J]. Mathematical Inequalities & Applications, 2015, 18(1):39-49. [NASA ADS] [MathSciNet] [Google Scholar]
- Milman E. On the mean-width of isotropic convex bodies and their associated Lp-centroid bodies [J]. International Mathematics Research Notices, 2015: 3408-3423. [Google Scholar]
- Pei Y N, Wang W D. Shephard type problems for general Lp-centroid bodies [J]. Journal of Inequalities & Applications, 2015, 2015(1): 287. [CrossRef] [Google Scholar]
- Wang W D, Lu F H, Leng G S. A type of monotonicity on the Lp centroid body and Lp projection body [J]. Mathematical Inequalities & Applications, 2005, 8(4): 735-742. [CrossRef] [MathSciNet] [Google Scholar]
- Wang W D, Leng G S. Inequalities of the quermassintegrals for the Lp-projection bodys and the Lp-centroid body [J]. Acta Mathematica Scientia, Series B, English Edition, 2010, 30(1): 359-368. [Google Scholar]
- Wang W D, Leng G S. Monotonicity of Lp-centroid body [J]. Journal of Systems Science and Mathematical Sciences, 2008, 28(2): 154-162. [Google Scholar]
- Yuan J, Zhao L Z, Leng G S. Inequalities for centroid body [J]. Taiwanese Journal of Mathematics, 2007, 11(5): 1315-1325. [Google Scholar]
- Grinberg E, Zhang G Y. Convolutions, transforms, and convex bodies [J]. Proceedings of the London Mathematical Society, 1999, 78(1): 77-115. [CrossRef] [MathSciNet] [Google Scholar]
- Abardia J, Bernig A. Projection bodies in complex vector spaces [J]. Advances in Mathematics, 2012, 227(2): 830-846. [Google Scholar]
- Abardia J. Difference bodies in complex vector spaces [J]. Journal of Functional Analysis, 2012, 263(11): 3588-3603. [CrossRef] [MathSciNet] [Google Scholar]
- Koldobsky A, Paouris G, Zymonopoulou M. Complex intersection bodies [J]. Journal of the London Mathematical Society, Second Series, 2013, 88(2): 538-562. [Google Scholar]
- Liu L J, Wang W, Huang Q Z. On polars of mixed complex projection bodies [J]. Bulletin of the Korean Mathematical Society, 2005, 52(2): 453-465. [Google Scholar]
- Li C, Wang W D. Inequalities for complex centroid bodies [J]. Acta Mathematica Hungarica, 2020, 161: 313-326. [CrossRef] [MathSciNet] [Google Scholar]
- Wang W, Liu L J. Complex Lp affine isoperimetric inequalities [J]. Advances in Applied Mathematics, 2021, 122: 102108. [CrossRef] [Google Scholar]
- Haberl C. Complex affine isoperimetric inequalities [J]. Calculus of Variations and Partial Differential Equations, 2019, 58(5): 169. [CrossRef] [Google Scholar]
- Wu Y C. On complex affine isoperimetric inequalities [J]. Mathematical Inequalities & Applications, 2021, 24(3): 655-678. [MathSciNet] [Google Scholar]
- Gardner R J. Geometric Tomography [M]. 2nd Edition. Cambridge: Cambridge University Press, 2006. [CrossRef] [Google Scholar]
- Schneider R. Convex Bodies: The Brunn-Minkowski Theory [M]. 2nd Edition. Cambridge: Cambridge University Press, 2014. [Google Scholar]
- Lutwak E. The Brunn-Minkowski-Firey theory I: Mixed volumes and the Minkowski problem [J]. The Journal of Differential Geometry, 1993, 38(1): 131-150. [Google Scholar]
- Lutwak E. The Brunn-Minkowski-Firey theory II: Affine and geominimal surface areas [J]. Advances in Mathematics, 1996, 118(1): 244-294. [CrossRef] [MathSciNet] [Google Scholar]
- Hardy G H, Littlewood J E, Pólya G. Inequalities [J]. Bulletin of the American Mathematical Society, 1953, 59: 411-412. [CrossRef] [MathSciNet] [Google Scholar]
- Lu F H, Leng G S. On Lp-Brunn-Minkowski type inequalities of convex bodies [J]. Boletín de la Sociedad Matemática Mexicana, Third Series, 2007, 13(1): 167-176. [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.