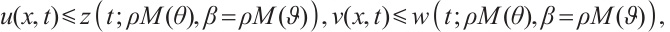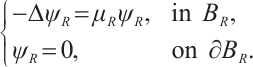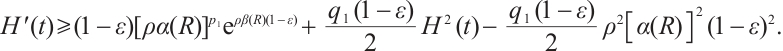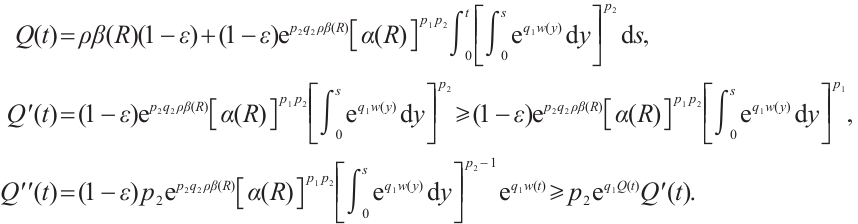| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 2, April 2025
|
|
|---|---|---|
| Page(s) | 111 - 117 | |
| DOI | https://doi.org/10.1051/wujns/2025302111 | |
| Published online | 16 May 2025 | |
Mathematics
CLC number: O175.26
Life Span of Solutions for a Class of Semilinear Parabolic Equations with Large Initial Values
一类大初值半线性抛物型方程解的生命跨度
College of Business, Xi’an International University, Xi’an 710077, Shaanxi, China
Received:
28
September
2024
In this paper, a class of semilinear parabolic equations with cross coupling of power and exponential functions and large initial values are studied. By constructing and solving ordinary differential equations, the upper and lower bounds on the solution life span of the equations are obtained.
摘要
研究了一类幂函数与指数函数交叉耦合,且具有大初值的半线性抛物方程组,通过构造和求解常微分方程的方法,得到了方程组解生命跨度的上下限。
Key words: semilinear parabolic equations / life span / comparative principle / blow up
关键字 : 半线性抛物型方程 / 生命跨度 / 比较原理 / 爆破
Cite this article: XUE Yingzhen, LI Yulin. Life Span of Solutions for a Class of Semilinear Parabolic Equations with Large Initial Values[J]. Wuhan Univ J of Nat Sci, 2025, 30(2): 111-117.
Biography: XUE Yingzhen, male, Professor, research direction: theory and application of partial differential equation. E-mail: xueyingzhen@xaiu.edu.cn
Foundation item: Supported by Key Project Funding for Shaanxi Higher Education Teaching Reform Research (23BZ078), Shaanxi Provincial Education Science Planning Project (SGH24Y2782), Shaanxi Provincial Social Science Foundation Program(2024D008), Key Projects of the Second Huang Yanpei Vocational Education Thought Research Planning Project (ZJS2024ZN026), Shaanxi Higher Education Society Key Projects(XGHZ2301), 2024 Annual Planning Project of the China Association for Non-Government Education (School Development Category) (CANFZG24095), and the Youth Innovation Team of Shaanxi Universities
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
In this article, we study the following system of semilinear parabolic equations
where  is a bounded domain in
is a bounded domain in  with smooth boundary
with smooth boundary  is a parameter,
is a parameter,  are nonnegative continuous functions in
are nonnegative continuous functions in 
Denote
We denote by  the maximal existence time of a classical solution
the maximal existence time of a classical solution  of Equations (1)-(4), that is
of Equations (1)-(4), that is
and we call  is the life span of
is the life span of  if
if  then we have
then we have
Equations (1)-(4) can be used to describe the processes of diffusion of heat and burning in two component continuous media conductivity, volume energy release, and nucleate blow up.
In recent decades, there are many research achievements on the life span of solutions determined by initial value has been considered, see Refs. [1-9]. Sato[1] studied the following system of semi-linear equations
and by using super-subsolution method and Kaplan method, he obtained expression of the span of solution when  . Xu et al[2] studied the following system of coupled parabolic equations with large initial values
. Xu et al[2] studied the following system of coupled parabolic equations with large initial values
then by constructing and solving a new ordinary parabolic equation (OPE) system, they had the accurate life span of solutions (blow up time) of the expression determined with the initial value.
Zhou et al[3] and Xiao[4] considered the following nonlinear parabolic system with large initial values
and they obtained the life span (or blow up time) and maximal existence time of blow up solutions. Zhou[5] investigated the upper and lower bound for the life span of solutions for the following parabolic system with large initial values,
and he obtained the upper and lower bound for the life span of solutions.
Other relevant achievements on the estimation of upper and lower bounds for blow up time see Refs. [6-9]. Current research mainly focuses on the nonlinear term being in the form of polynomial or exponential functions. Then, can we obtain results similar to those in Refs. [2,5] when the nonlinear term is cross coupled with power and exponential functions? This article studies the upper and lower bounds of the life span of equations (1)-(4), cleverly resolving the difficulty of integration when multiplying power and exponential functions. The conclusion can better describe the situation where the reaction rate of the medium is inconsistent during the combustion and diffusion process of porous media flow and two com- ponent continuous media.
The arrangement of this article is as follows: in Section 1, two important theorems of this article are presented. In Section 2, in order to prove the theorems, a system of ordinary differential equations (ODE) is constructed and solved. In Section 3, the main theorems are proved in detail.
1 Main Results
In this section, we state the following main results.
Theorem 1 Let  suppose that
suppose that  satisfy
satisfy 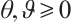 in
in 
 on
on  .
.
(i) If  then we have
then we have
(ii) If  then we have
then we have
Theorem 2 Let  suppose that
suppose that  satisfy
satisfy  in
in 
 on
on  .
.
(i) If  then we have
then we have
(ii) If  then we have
then we have
2 Blow up Time of ODE System
In this section, we consider the ODE system as follows:
where  are two nonnegative numbers.
are two nonnegative numbers.
Lemma 1 If the equations (5)-(7) have solutions for the following form,
where

 represent the inverse functions of
represent the inverse functions of  and
and  with respect to the first variable, respectively. Then the life span of
with respect to the first variable, respectively. Then the life span of  is
is 
Proof Let the first equations of (5)-(7) divide the second one, then it gives  integrating the equation over
integrating the equation over 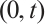 above, we can obtain
above, we can obtain
Hence we have
Substituting those equalities in the equations (5)-(7), we set that  satisfies the initial value problem
satisfies the initial value problem
Integrating the first equation above over  , we can show
, we can show
Hence we obtain
This implies that the life span  of (z,w) is
of (z,w) is
By using the change of variables
it is easy to obtain that
that is 
3 Proof of Main Results
In this section, we prove the main results by first proving Theorem 1.
Proof Choosing  by virtue of comparison principle, see also Lemma 3.1 in Ref. [6], it follows that
by virtue of comparison principle, see also Lemma 3.1 in Ref. [6], it follows that
for  and
and 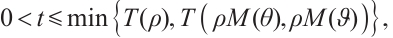 this implies
this implies 
If  we obtain
we obtain
Multiplying  to both sides above inequality and taking
to both sides above inequality and taking  we obtain the result (i) of Theorem 1 by Lebesgue theorem[10].
we obtain the result (i) of Theorem 1 by Lebesgue theorem[10].
If  we have
we have
Multiplying  to both sides above inequality and taking
to both sides above inequality and taking  we obtain the result (ii) of Theorem 1 by Leesgue theorem[10]. This completes the proof of the Theorem 1.
we obtain the result (ii) of Theorem 1 by Leesgue theorem[10]. This completes the proof of the Theorem 1.
The following proof proves Theorem 2.
Proof In order to prove this Lemma, we employ Kaplan's method[7]. First we consider the case of  assume without loss generality that
assume without loss generality that  define by
define by 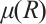 the first eigenvalue of
the first eigenvalue of  in the ball
in the ball  and
and 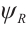 is the corresponding eigenfunction.
is the corresponding eigenfunction.
Thus, we have
Assuming that  it is easy to note that
it is easy to note that 
Let  we set
we set
Since 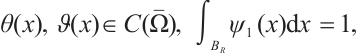 we obtain
we obtain 
Multiplying the equations of (1)-(4) by  integrating by parts and using Jensen inequality[10], we have
integrating by parts and using Jensen inequality[10], we have
By using the derivative formula of the product of two terms and performing simple calculations, we obtain
Integrating these inequalities over  we see that
we see that
Substituting the second inequality into the first, it follows that
where, when  we use the following inequality
we use the following inequality
We fix  and take
and take  such that
such that  then we have
then we have
We set
Since  we see that
we see that
Integrating these inequalities over  it follows that
it follows that
Dividing the left hand side by the right hand side and integrating over  we have
we have
We take large  such that
such that
Then  blows up at time
blows up at time  hence we get
hence we get
Therefore, by  and Lebesgue's theorem, it follows that
and Lebesgue's theorem, it follows that
Taking  and then
and then  we obtain the result (i) of Theorem 2.
we obtain the result (i) of Theorem 2.
Next we consider the case of  Similarly, we have
Similarly, we have
We fix  and take
and take  such that
such that  then we have
then we have
Taking 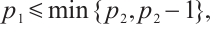 we set
we set
Integrating these inequalities over  it follows that
it follows that
Dividing the left hand side by the right hand side and integrating over  we obtain
we obtain
We take large  such that
such that
Then  blow up at time
blow up at time  hence we get
hence we get
Therefore, by Lebesgue theorem[10], it follows that
taking 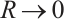 and then
and then  we obtain the result (ii) of Theorem 2. This completes the proof of Theorem 2.
we obtain the result (ii) of Theorem 2. This completes the proof of Theorem 2.
References
- Sato S. Life span of solutions with large initial data for a semilinear parabolic system[J]. Journal of Mathematical Analysis and Applications, 2011, 380(2): 632-641. [Google Scholar]
- Xu X J, Ye Z. Life span of solutions with large initial data for a class of coupled parabolic systems[J]. Zeischrift für angewamde Mathematik and physik, 2013, 64(3): 705-717. [Google Scholar]
- Zhou S, Yang Z D. Life span of solutions with large initial data for a semilinear parabolic systems[J]. Journal of Mathematical Research with Applications, 2015, 35(1): 103-109. [Google Scholar]
- Xiao F. Life span of solutions for a class of parabolic system with large initial data[J]. Acta Mathematica Scientia, 2016, 36A(4): 672-680. [Google Scholar]
- Zhou S. Life span of solutions with large initial data for a semilinear parabolic system coupling exponential reaction terms[J]. Boundary Value Problems, 2019, 154: 1-8. [Google Scholar]
- Chen H W. Global existence and blow up for a nonlinear reaction diffusion system[J]. Journal of Mathematical Analysis and Applications, 1997, 212(2): 481-492. [Google Scholar]
- Kaplan S. On the growth of solutions of quasi-linear parabolic equations[J]. Communications on Pure and Applied Mathematics, 1963, 16(3): 305-330. [Google Scholar]
- Xue Y Z. Lower bound of blow up time for solutions of a class of cross coupled porous media equations[J]. Wuhan University Journal of Natural Sciences, 2021, 26(4): 289-294. [Google Scholar]
- Leng Y, Nie Y, Zhou Q. Asymptotic behavior of solutions to a class of coupled parabolic systems[J]. Boundary Value Problems, 2019, 68: 1-11. [Google Scholar]
- Hu S Z. An interesting proof of Lebesgue theorem and Riemann inerability of functions[J]. Journal of Fuyang Teachers College (Natural Science), 2000, 17(1): 56-58(Ch). [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.