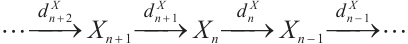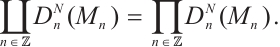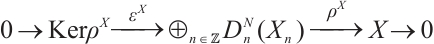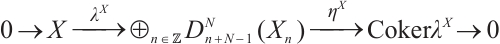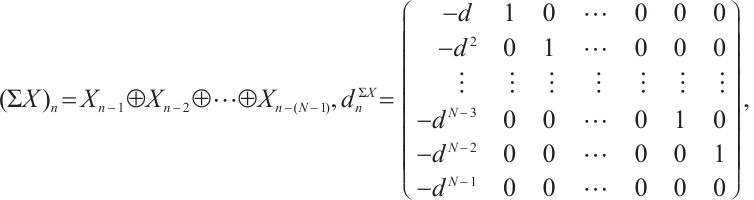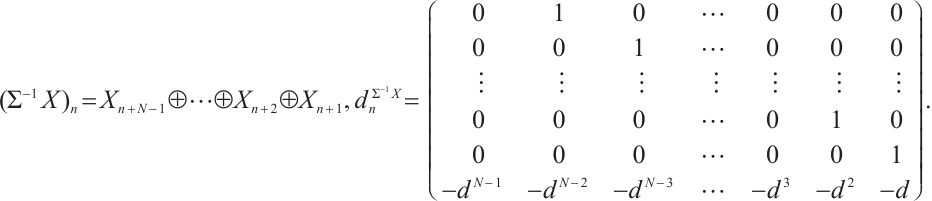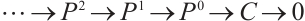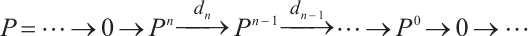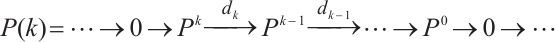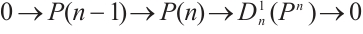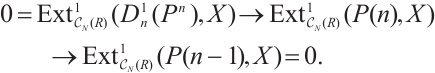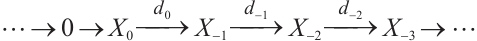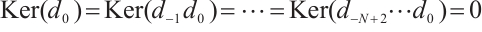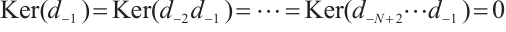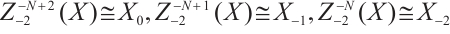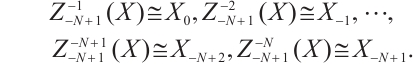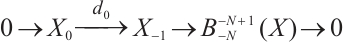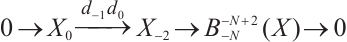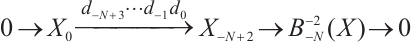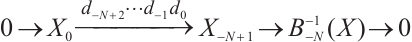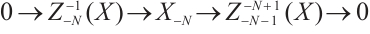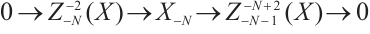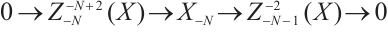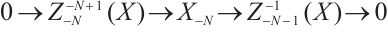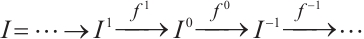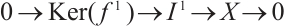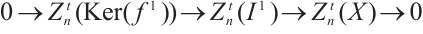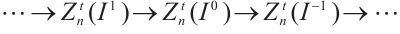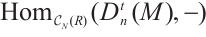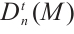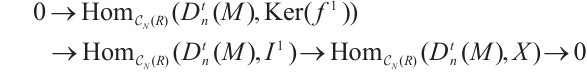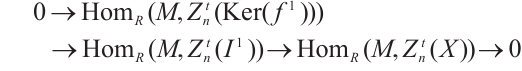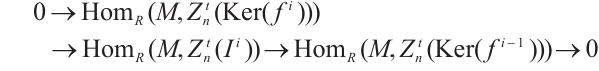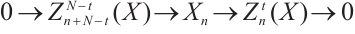| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 2, April 2025
|
|
|---|---|---|
| Page(s) | 133 - 138 | |
| DOI | https://doi.org/10.1051/wujns/2025302133 | |
| Published online | 16 May 2025 | |
Mathematics
CLC number: O153.3
Absolutely Clean N-Complexes
绝对Clean N-复形
College of Mathematics and Computer Science, Northwest Minzu University, Lanzhou 730030, Gansu, China
† Corresponding author. E-mail: lubo55@126.com
Received:
10
April
2024
The notion of absolutely clean N-complexes is studied. We show that an N-complex 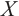 is absolutely clean if and only if
is absolutely clean if and only if 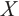 is N-exact and
is N-exact and 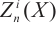 is an absolutely clean module for each
is an absolutely clean module for each 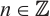 and
and 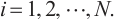 In particular, we prove that a bounded above N-complex
In particular, we prove that a bounded above N-complex 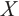 is absolutely clean if and only if
is absolutely clean if and only if 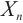 is an absolutely clean module for each
is an absolutely clean module for each 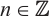 . We also show that under certain hypotheses, an N-complex
. We also show that under certain hypotheses, an N-complex  is Gorenstein AC-injective if and only if
is Gorenstein AC-injective if and only if 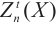 is a Gorenstein AC-injective module for each
is a Gorenstein AC-injective module for each 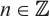 and
and 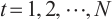 .
.
摘要
研究了绝对clean N-复形的概念,证明了N-复形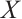 是绝对clean的当且仅当
是绝对clean的当且仅当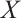 是N-正合的并且对任意的
是N-正合的并且对任意的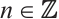 和
和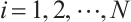 ,
,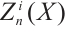 是绝对clean模。特别地,证明了上有界N-复形
是绝对clean模。特别地,证明了上有界N-复形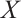 是绝对clean的当且仅当
是绝对clean的当且仅当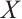 是N-正合的并且对任意的
是N-正合的并且对任意的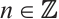 ,
,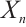 是绝对clean 模。证明了一定条件下N-复形
是绝对clean 模。证明了一定条件下N-复形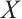 是Gorenstein AC-内射的当且仅当对任意的
是Gorenstein AC-内射的当且仅当对任意的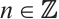 和
和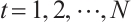 ,
,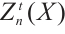 是Gorenstein AC-内射模。
是Gorenstein AC-内射模。
Key words: absolutely clean module / absolutely clean N-complex / Gorenstein AC-injective N-complex
关键字 : 绝对clean模 / 绝对clean N-复形 / Gorenstein AC-内射N-复形
Cite this article: HAN Xia, WANG Xin, LU Bo. Absolutely Clean N-Complexes[J]. Wuhan Univ J of Nat Sci, 2025, 30(2): 133-138.
Biography: HAN Xia, female, Master candidate, research direction: homological algebra. E-mail: y221530320@stu.xbmu.edu.cn
Foundation item: Supported by the National Natural Science Foundation of China (12061061), Fundamental Research Funds for the Central Universities (31920230173), Longyuan Young Talents of Gansu Province, and Young Talents Team Project of Gansu Province (2025QNTD49)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
A module 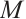 is called type
is called type 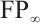 if
if 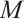 has a projective resolution by finitely generated projective modules. This concept is a generalization of finitely generated modules and finitely presented modules, which is studied by Bravo et al[1]. Also a module
has a projective resolution by finitely generated projective modules. This concept is a generalization of finitely generated modules and finitely presented modules, which is studied by Bravo et al[1]. Also a module 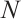 is called
is called 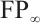 -injective or absolutely clean if
-injective or absolutely clean if 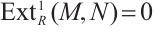 for all modules
for all modules 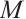 of type
of type 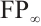 , these modules have properties that injective modules only have over Noetherian rings. Specifically, if
, these modules have properties that injective modules only have over Noetherian rings. Specifically, if 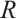 is left Noetherian, the modules of type
is left Noetherian, the modules of type 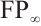 are precisely the finitely generated modules.
are precisely the finitely generated modules.
The category of complexes plays an important role in the theory of homological algebra, and many results of the category of modules have been generalized to the category of complexes. As we know, in the category of complexes, the relationship between complexes and its level modules and cycle modules is an important research topic. For example, a complex is injective if and only if it is exact and each cycle module is injective. A complex 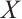 is absolutely clean if and only if
is absolutely clean if and only if 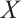 is exact and each
is exact and each 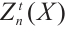 is an absolutely clean module for each
is an absolutely clean module for each 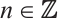 and
and 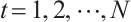 . A complex
. A complex 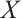 is Gorenstein AC-injective if and only if
is Gorenstein AC-injective if and only if 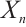 is a Gorenstein AC-injective module and
is a Gorenstein AC-injective module and 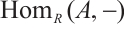 is exact for any absolutely clean complex
is exact for any absolutely clean complex  [2].
[2].
The notion of N-complexes was introduced by Mayer in his study of simplicial complexes[3-4], that is, it satisfies differentials  . The category of N-complexes is consistent with the category of complexes whenever
. The category of N-complexes is consistent with the category of complexes whenever  . In 1996, Kapranov[5], Dubois-Violette and Kerner[6] gave an abstract framework of homological theory of N-complexes. Since then, the N-complexes have been concerned by many authors, for example Refs.[7-11]. Recently, Lu[12] introduced the concept of FP-injective N-complexes, which has shown that an N-complex
. In 1996, Kapranov[5], Dubois-Violette and Kerner[6] gave an abstract framework of homological theory of N-complexes. Since then, the N-complexes have been concerned by many authors, for example Refs.[7-11]. Recently, Lu[12] introduced the concept of FP-injective N-complexes, which has shown that an N-complex 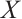 is FP-injective if and only if
is FP-injective if and only if 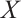 is N-exact and
is N-exact and 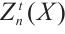 is an FP-injective module for each
is an FP-injective module for each 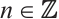 and
and 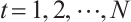 .
.
In present paper, we establish relationships between the absolutely clean N-complex and its level modules and cycle modules. And from this, we prove that under certain hypotheses, an N-complex 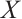 is Gorenstein AC-injective if and only if
is Gorenstein AC-injective if and only if 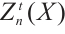 is a Gorenstein AC-injective module for each
is a Gorenstein AC-injective module for each 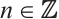 and
and 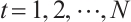 .
.
More precisely, our results can be stated as follows:
Theorem 1 Let 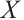 be an N-complex. Then
be an N-complex. Then 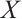 is absolutely clean if and only if
is absolutely clean if and only if 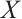 is N-exact and
is N-exact and 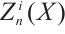 is an absolutely clean module for each
is an absolutely clean module for each 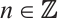 and
and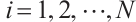 .
.
As an application of Theorem 1, the following result is established.
Proposition 1 Let 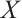 be a bounded above N-complex. Then
be a bounded above N-complex. Then 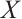 is absolutely clean if and only if
is absolutely clean if and only if 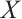 is N-exact and
is N-exact and 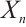 is an absolutely clean module for
is an absolutely clean module for 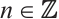 .
.
It is well known that an N-complex 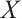 is Gorenstein AC-injective if and only if
is Gorenstein AC-injective if and only if 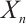 is a Gorenstein AC-injective module and
is a Gorenstein AC-injective module and 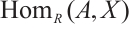 is N-exact for any absolutely clean N-complex
is N-exact for any absolutely clean N-complex 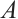 [9]. As another application of Theorem 1, we also obtain the following result, which extends the above classical result to the Gorenstein AC-injective N-complexes.
[9]. As another application of Theorem 1, we also obtain the following result, which extends the above classical result to the Gorenstein AC-injective N-complexes.
Proposition 2 Let 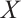 be an N-exact N-complex with
be an N-exact N-complex with 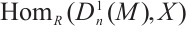 N-exact for any absolutely clean module
N-exact for any absolutely clean module 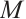 . Then
. Then 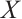 is a Gorenstein AC-injective N-complex if and only if
is a Gorenstein AC-injective N-complex if and only if 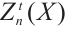 is a Gorenstein AC-injective module for each
is a Gorenstein AC-injective module for each 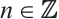 and
and 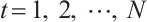 .
.
1 Preliminaries
Throughout this paper, unless stated otherwise, 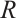 denotes an associative ring with an identity and by the term "module" we always mean a left
denotes an associative ring with an identity and by the term "module" we always mean a left 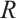 -module and use
-module and use 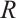 -
- to denote the category of left
to denote the category of left  -modules.
-modules.
This section is devoted to recalling some notions and basic consequences for use throughout this paper. For terminology we shall follow Refs. [7] and [10] when working with N-complexes.
By an N-complex 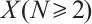 we mean a sequence of left
we mean a sequence of left 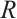 -modules
-modules
satisfying 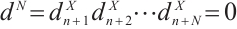 for any
for any 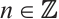 . That is, composing any N-consecutive morphisms gives
. That is, composing any N-consecutive morphisms gives 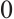 . So a
. So a 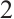 -complex is a chain complex in the usual sense. A chain map or simply map
-complex is a chain complex in the usual sense. A chain map or simply map 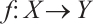 of N-complexes is a collection of morphisms
of N-complexes is a collection of morphisms 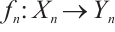 making all the rectangles commute. In this way, we get a category of N-complexes of left
making all the rectangles commute. In this way, we get a category of N-complexes of left 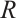 -modules, denoted by
-modules, denoted by  , whose objects are N-complexes and whose morphisms are chain maps. This is an abelian category having enough projectives and injectives. Let
, whose objects are N-complexes and whose morphisms are chain maps. This is an abelian category having enough projectives and injectives. Let 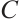 and
and 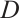 be N-complexes. We use
be N-complexes. We use 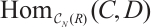 to denote the Abelian group of morphisms from
to denote the Abelian group of morphisms from 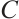 and
and 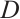 and
and 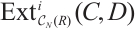 for
for 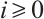 to denote the groups we get from the right derived functor of
to denote the groups we get from the right derived functor of 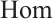 .
.
For an N-complex 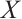 , there are
, there are 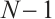 choices for homology. Indeed for
choices for homology. Indeed for 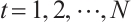 , we define
, we define 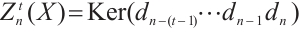 and
and 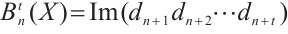 . In particular, we have
. In particular, we have 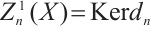 ,
,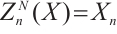 and
and 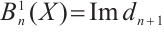 ,
,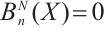 . Finally, we define
. Finally, we define 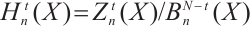 the amplitude homology objects of
the amplitude homology objects of 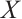 for all
for all 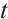 . We say
. We say 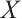 is N-exact, or just exact, if
is N-exact, or just exact, if 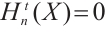 for all
for all 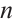 and
and 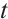 .
.
An N-complex 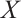 is called bounded, if there is only a finite number
is called bounded, if there is only a finite number 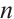 such that
such that 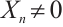 ; if
; if 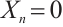 when
when 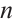 is sufficiently large, which is called bounded above. Similarly, we can define lower bounded N-complexes. As we know, an N-complex
is sufficiently large, which is called bounded above. Similarly, we can define lower bounded N-complexes. As we know, an N-complex 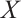 is called finitely generated if
is called finitely generated if 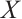 is bounded and
is bounded and 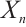 is a finitely generated module for each
is a finitely generated module for each 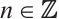 .
.
Unless stated otherwise, in the following complexes will always denote 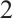 -complexes. Given a module
-complexes. Given a module 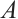 , we define N-complexes
, we define N-complexes 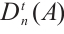 for
for 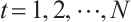 , as follows:
, as follows: 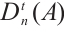 consists of
consists of 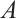 in degrees
in degrees 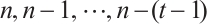 , all joined by identity morphisms, and
, all joined by identity morphisms, and 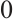 in every other degree. Let
in every other degree. Let 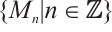 be objects of modules. Then
be objects of modules. Then 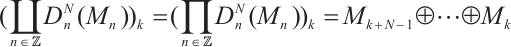 for all
for all 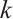 . Therefore,
. Therefore,
Two chain maps 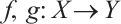 are called chain homotopic, or simply homotopic if there exists a collection of morphisms
are called chain homotopic, or simply homotopic if there exists a collection of morphisms 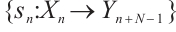 such that
such that
If 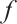 and
and 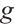 are homotopic, then we write
are homotopic, then we write 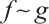 . We call a chain map
. We call a chain map 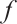 null homotopic if
null homotopic if 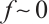 . There exists an additive category
. There exists an additive category 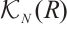 , called the homotopy category of N-complexes, whose objects are the same as those of
, called the homotopy category of N-complexes, whose objects are the same as those of 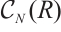 and whose
and whose 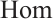 sets are the equivalence classes of
sets are the equivalence classes of 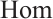 sets in
sets in 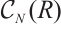 . An isomorphism in
. An isomorphism in 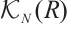 is called a homotopy equivalence. Let
is called a homotopy equivalence. Let 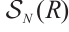 be the collection of sequences
be the collection of sequences 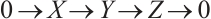 of morphisms in
of morphisms in 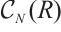 such that
such that 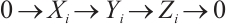 is split exact in
is split exact in 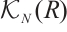 for any integer
for any integer 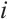 .
.
Following Ref.[8], let 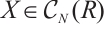 , we have morphisms
, we have morphisms 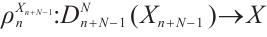 and
and 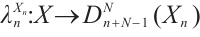 . Set
. Set 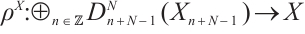 and
and 
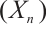 . Then we have the following exact sequences in
. Then we have the following exact sequences in 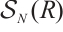 ,
,
and
Now we define functors 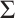 ,
,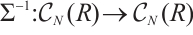 by
by 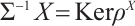 and
and 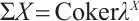 in the exact sequences above. Then
in the exact sequences above. Then 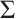 and
and 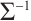 induce the suspension functor and its quasi-inverse of the triangulated category
induce the suspension functor and its quasi-inverse of the triangulated category 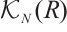 . On the other hand, we define the shift functor
. On the other hand, we define the shift functor 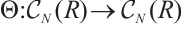 by
by 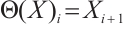 and
and 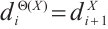 for
for 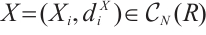 . The N-complex
. The N-complex 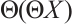 is denoted as
is denoted as 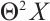 and inductively we define
and inductively we define 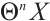 for all
for all 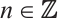 . This induces the shift functor
. This induces the shift functor 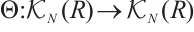 which is a triangle functor. Unlike classical case,
which is a triangle functor. Unlike classical case, 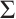 does not coincide with
does not coincide with  .
.
Following Refs. [8] or [10], for any N-complex 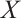 ,
, 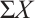 and
and 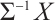 are given by the following explicit description,
are given by the following explicit description,
2 Main Results
In this section, we investigate the concept of absolutely clean N-complexes and give some equivalence characterizations of absolutely clean N-complexes. In particular, we prove that an N-complex 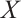 is absolutely clean if and only if
is absolutely clean if and only if 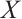 is N-exact and
is N-exact and 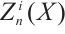 is an absolutely clean module for each
is an absolutely clean module for each 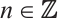 and
and 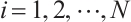 .
.
Definition 1 An N-complex 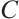 is of type
is of type 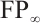 if
if 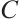 has a projective resolution
has a projective resolution 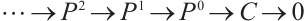 by finitely generated projective N-complexes
by finitely generated projective N-complexes 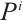 for
for 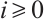 .
.
Proposition 3 An N-complex 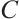 is of type
is of type 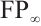 if and only if it is bounded and each
if and only if it is bounded and each 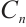 is a module of type
is a module of type 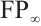 .
.
Proof Sufficiency. Let 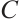 be of type
be of type 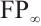 . Then it must be finitely generated, so it is bounded. We also see that each N-complex
. Then it must be finitely generated, so it is bounded. We also see that each N-complex 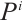 must consist of finitely generated projective modules in each degree by the definition of N-complex of type
must consist of finitely generated projective modules in each degree by the definition of N-complex of type 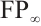 . So we get that each
. So we get that each 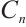 is a module of type
is a module of type 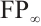 .
.
Necessity. Suppose 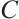 is bounded and each
is bounded and each 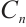 is a module of type
is a module of type  , we can construct a surjection
, we can construct a surjection  where
where  is a finitely generated projective N-complex. Set
is a finitely generated projective N-complex. Set 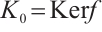 and note that it also must be bounded. Since each
and note that it also must be bounded. Since each 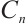 must also be finitely presented, it follows that each
must also be finitely presented, it follows that each 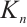 is finitely generated. Thus
is finitely generated. Thus 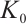 is finitely generated, and we can again construct a surjection
is finitely generated, and we can again construct a surjection 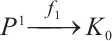 where
where 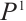 is a finitely generated projective N-complex. Set
is a finitely generated projective N-complex. Set 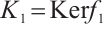 and note that
and note that 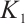 must be bounded. Since each
must be bounded. Since each 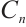 must be of type
must be of type 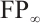 , it follows that
, it follows that 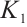 must also be finitely generated N-complex. Continuing this way, we can construct a projective resolution
must also be finitely generated N-complex. Continuing this way, we can construct a projective resolution
where each 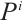 is a finitely generated projective N-complex.
is a finitely generated projective N-complex.
Remark 1 1) If 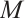 is a module of type
is a module of type 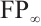 , then
, then 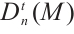 is an N-complex of type
is an N-complex of type 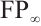 for each
for each 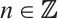 and
and 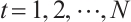 .
.
2) An N-complex of type 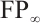 is finitely generated.
is finitely generated.
Definition 2 An N-complex 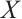 is said to be absolutely clean if
is said to be absolutely clean if 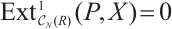 for all N-complexes
for all N-complexes 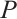 of type
of type 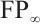 .
.
Remark 2 1) If 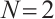 , then absolutely clean N-complexes are precisely absolutely clean complex.
, then absolutely clean N-complexes are precisely absolutely clean complex.
2) The class of absolutely clean N-complexes is closed under direct products, summands and direct limits.
3) 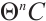 is absolutely clean for any absolutely clean N-complex
is absolutely clean for any absolutely clean N-complex 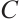 and
and 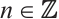 .
.
4) The class of absolutely clean N-complexes is coresolving. For any absolutely clean N-complex 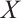 and
and 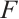 of type
of type 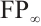 , we have
, we have 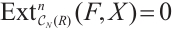 for all
for all 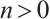 .
.
5) The class of absolutely clean N-complexes is closed under clean N-subcomplexes and clean quotients.
It is well known that an N-complex 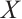 is injective if and only if
is injective if and only if 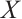 is N-exact and
is N-exact and 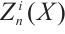 is an injective module for each
is an injective module for each 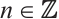 and
and 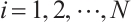 . In the following, we will generalize this characterization to the absolutely clean N-complexes. Firstly, we need to make the following preparations.
. In the following, we will generalize this characterization to the absolutely clean N-complexes. Firstly, we need to make the following preparations.
Lemma 1 An N-complex 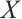 is absolutely clean if and only if
is absolutely clean if and only if 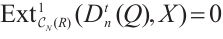 for all modules
for all modules  of type
of type 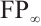 and
and 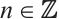 and
and 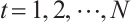 .
.
Proof Sufficiency. It is trivial.
Necessity. Without losing generality, we take 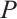 has the following form:
has the following form:
with each 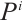 a module of type
a module of type 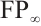 for
for 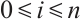 .
.
For any 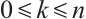 , we put
, we put
Then 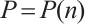 . In the following, we prove the result by using induction on
. In the following, we prove the result by using induction on 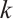 . For
. For 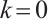 , by the assumption,
, by the assumption,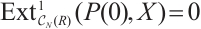 . Assume that
. Assume that 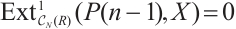 . Applying the functor
. Applying the functor 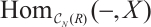 to the exact sequence
to the exact sequence
yields the following exact sequence
Then 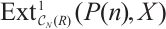 , as desired.
, as desired.
Lemma 2[11] Let 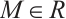 -
-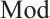 ,
, 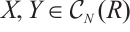 and
and 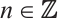 ,
,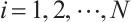 . Then we have the following natural isomorphisms:
. Then we have the following natural isomorphisms:
1) 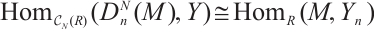 .
.
2) 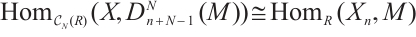 .
.
3) 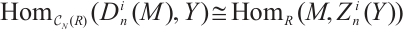 .
.
4)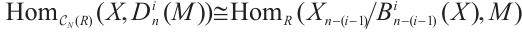 .
.
5) 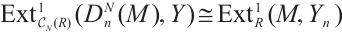 .
.
6) 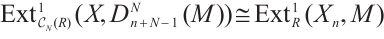 .
.
7) If 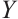 is N-exact, then
is N-exact, then 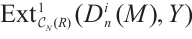
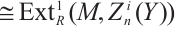 .
.
8) If 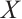 is N-exact, then
is N-exact, then 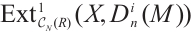
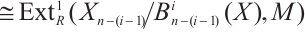 .
.
Following Ref. [5], let 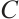 and
and 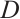 be N-complexes of left
be N-complexes of left 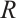 -modules. We will denote by
-modules. We will denote by 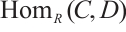 the sequence of Abelian groups with
the sequence of Abelian groups with 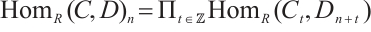 and such that if
and such that if 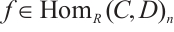 then
then 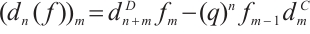 , where
, where 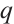 is a N-th root of unity,
is a N-th root of unity, 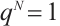 and
and 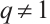 . Then
. Then  is also an N-complex.
is also an N-complex. 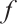 is called a chain map of degree
is called a chain map of degree 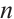 if
if 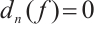 . A chain map of degree
. A chain map of degree 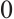 is called a morphism.
is called a morphism.
Lemma 3[13] Let 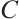 and
and 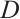 be N-complexes. Then
be N-complexes. Then 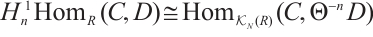 . In particular,
. In particular, 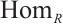
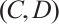 is N-exact if and only if
is N-exact if and only if  , i.e.,
, i.e.,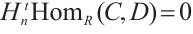 is equivalent to
is equivalent to 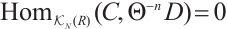 for
for  and
and  .
.
Proof of Theorem 1
Sufficiency. Let 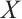 be an absolutely clean N-complex. Then
be an absolutely clean N-complex. Then 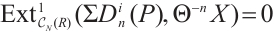 for any module
for any module 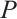 of type
of type  ,
, 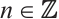 and
and 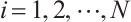 . This implies that N-complex
. This implies that N-complex 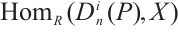 is N-exact[13]. Note that
is N-exact[13]. Note that 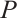 is of type
is of type 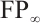 . It follows that
. It follows that 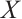 must be an N-exact N-complex. Also,
must be an N-exact N-complex. Also, 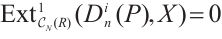 for all modules
for all modules 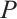 of type
of type 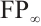 ,
, 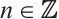 and
and 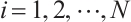 . Using Lemma 2, we get
. Using Lemma 2, we get 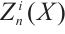 is an absolutely clean module for
is an absolutely clean module for 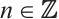 and
and 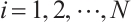 .
.
Necessity. It follows by Lemma 1 and Lemma 2.
Then the following result can be obtained by Theorem 1.
Corollary 1 If an N-complex 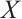 is absolutely clean, then
is absolutely clean, then 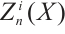 is an absolutely clean module for each
is an absolutely clean module for each 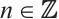 and
and 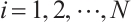 . Moreover,
. Moreover,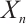 is an absolutely clean module for each
is an absolutely clean module for each 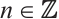 .
.
Corollary 2 A module 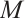 is absolutely clean if and only if the N-complex
is absolutely clean if and only if the N-complex 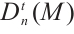 is absolutely clean for each
is absolutely clean for each 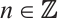 and
and 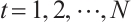 .
.
In the following, we obtain a result for bounded above N-complex 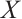 .
.
Proof of Proposition 1
Sufficiency. Obviously, 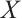 is N-exact and
is N-exact and 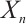 is an absolutely clean module for
is an absolutely clean module for 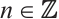 by Theorem 1 and Corollary 1.
by Theorem 1 and Corollary 1.
Necessity. Assume that 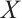 has the following form:
has the following form:
Since 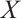 is N-exact,
is N-exact,
This implies that 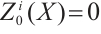 for
for  and
and 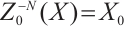 . Also we have
. Also we have
Then 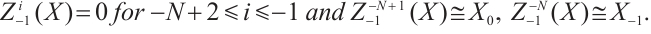
Similarly, 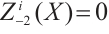 for
for 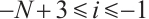 and
and
Then 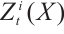 is absolutely clean for
is absolutely clean for 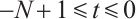 ,
, 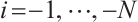 .
.
Note that
are exact. This implies that 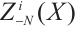 is absolutely clean for
is absolutely clean for 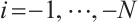 .
.
Using exact sequences
we can obtain 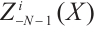 is absolutely clean for
is absolutely clean for 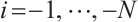 .
.
We also obtain 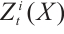 is absolutely clean for
is absolutely clean for 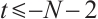 ,
,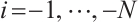 , by a similar method. Thus
, by a similar method. Thus 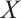 is absolutely clean by Theorem 1.
is absolutely clean by Theorem 1.
As we know, absolutely clean N-complex is important for the characterization of Gorenstein AC-injective N-complexes. An N-complex 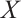 is Gorenstein AC-injective if and only if
is Gorenstein AC-injective if and only if 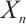 is a Gorenstein AC-injective module and
is a Gorenstein AC-injective module and 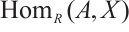 is N-exact for any absolutely clean N-complex
is N-exact for any absolutely clean N-complex 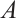 [9]. Next we obtain an equivalent characterization for N-exact absolutely clean N-complex in Gorenstein AC-injective N-complexes.
[9]. Next we obtain an equivalent characterization for N-exact absolutely clean N-complex in Gorenstein AC-injective N-complexes.
Proof of Proposition 2
Sufficiency. From the definition of the Gorenstein AC-injective N-complexes[8], there is an exact sequence of injective N-complexes
with 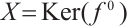 and which remains exact after applying
and which remains exact after applying 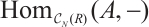 for any absolutely clean N-complex
for any absolutely clean N-complex 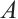 . Since
. Since 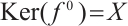 and
and 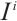 are N-exact, we have
are N-exact, we have 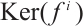 is N-exact for all
is N-exact for all  .
.
For the exact sequence
according to Ref. [14] we have the following exact sequence
Thus there is an exact sequence of injective modules
with 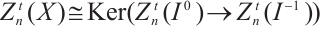 . Next we only show that
. Next we only show that 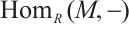 applying the sequence (18) exact for any absolutely clean module
applying the sequence (18) exact for any absolutely clean module  .
.
Let  be an absolutely clean module and
be an absolutely clean module and 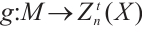 be a morphism of modules. Since
be a morphism of modules. Since 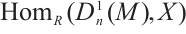 is N-exact, there exists a morphism
is N-exact, there exists a morphism 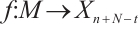 such that the following diagram commute (Fig. 1).
such that the following diagram commute (Fig. 1).
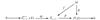 |
Fig. 1 The commutative diagram of 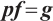 Note that |
It follows from Lemma 2
is exact. Similarly, we can prove that
is exact. Hence,  applying the sequence (18) exact.
applying the sequence (18) exact.
Necessity. Note that there is an exact sequence
and  and
and  are Gorenstein AC-injective modules, this implies
are Gorenstein AC-injective modules, this implies 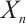 is a Gorenstein AC-injective module for each
is a Gorenstein AC-injective module for each 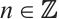 . Next we need to prove that
. Next we need to prove that 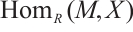 is N-exact for any absolutely clean N-complex
is N-exact for any absolutely clean N-complex 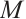 . The proof is similar to Theorem 3.2 in Ref. [2]. Thus
. The proof is similar to Theorem 3.2 in Ref. [2]. Thus  is a Gorenstein AC-injective N-complex.
is a Gorenstein AC-injective N-complex.
References
- Bravo D, Gillespie J, Hovey M. The stable module category of a general ring[EB/OL]. [2014-06-25]. https://arxiv.org/abs/q-alg/1405.5768. [Google Scholar]
- Bravo D, Gillespie J. Absolutely clean, level, and Gorenstein AC-injective complexes[J]. Communications in Algebra, 2016, 44(5): 2213-2233. [Google Scholar]
- Mayer W. A new homology theory I[J]. Annals of Mathematics, 1942, 43(2): 370-380. [Google Scholar]
- Mayer W. A new homology theory II[J]. Annals of Mathematics, 1942, 43(3): 594-605. [Google Scholar]
- Kapranov M M. On the q-analog of homological algebra[EB/OL]. [1996-11-04]. https://arxiv.org/abs/q-alg/9611005. [Google Scholar]
- Dubois-Violette M, Kerner R. Universal q-dierential calculus and q-analog of homological algebra[EB/OL]. [1996-08-30]. https://arxiv.org/abs/q-alg/9608026. [Google Scholar]
- Gillespie J. The homotopy category of N-complexes is a homotopy category[J]. Journal of Homotopy and Related Structures, 2015, 10(1): 93-106. [Google Scholar]
- Iyama O, Kato K, Miyachi J I. Derived categories of N-complexes[J]. Journal of the London Mathematical Society, 2017, 96(3): 687-716. [Google Scholar]
- Lu B. Gorenstein objects in the category of N-complexes[J]. Journal of Algebra and Its Applications, 2021, 20(10): 2150174. [CrossRef] [Google Scholar]
- Yang X Y, Ding N Q. The homotopy category and derived category of N-complexes[J]. Journal of Algebra, 2015, 426: 430-476. [Google Scholar]
-
Yang X Y, Gao T Y. Cotorsion pairs in
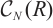 [J]. Algebra Colloquium, 2017, 24(4): 577-602.
[Google Scholar]
[J]. Algebra Colloquium, 2017, 24(4): 577-602.
[Google Scholar]
- Lu B. FP-injective objective in the category of N-complexes[J]. Indian Journal of Pure and Applied Mathematics, 2024, 55(1): 242-255. [Google Scholar]
- Lu B, Di Z X. Gorenstein cohomology of N-complexes[J]. Journal of Algebra and Its Applications, 2020, 19(9): 2050174. [Google Scholar]
- Lu B. Cartan-Eilenberg Gorenstein projective N-complexes[J]. Communications in Algebra, 2021, 49(9): 3810-3824. [Google Scholar]
All Figures
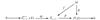 |
Fig. 1 The commutative diagram of  Note that |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.