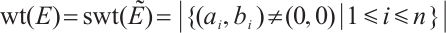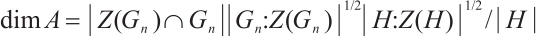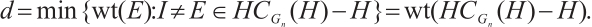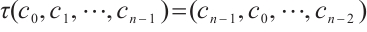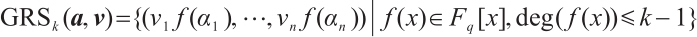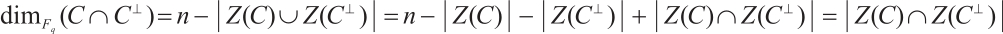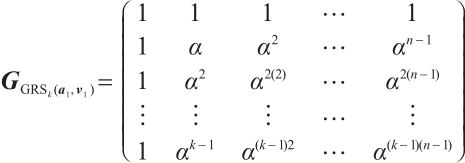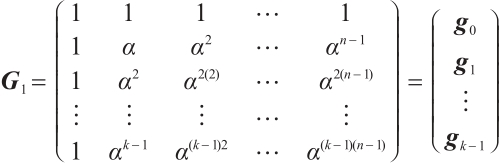| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 29, Number 1, February 2024
|
|
|---|---|---|
| Page(s) | 38 - 44 | |
| DOI | https://doi.org/10.1051/wujns/2024291038 | |
| Published online | 15 March 2024 | |
Mathematics
CLC number: O236.2
Three New Classes of Subsystem Codes
1
School of Mathematics and Physics, Hubei Polytechnic University, Huangshi 435003, Hubei, China
2
College of Arts and Science, Hubei Normal University, Huangshi 435003, Hubei, China
Received:
18
May
2023
In this paper, we construct three classes of Clifford subsystem maximum distance separable (MDS) codes based on Reed-Solomon codes and extended generalized Reed-Solomon codes over finite fields  for specific code lengths. Moreover, our Clifford subsystem MDS codes are new because their parameters differ from the previously known ones.
for specific code lengths. Moreover, our Clifford subsystem MDS codes are new because their parameters differ from the previously known ones.
Key words: Clifford subsystem codes / Reed-Solomon codes / generator matrices
Cite this article: LI Hui, LIU Xiusheng, HU Peng. Three New Classes of Subsystem Codes[J]. Wuhan Univ J of Nat Sci, 2024, 29(1): 38-44.
Biography: LI Hui, female, Master, Lecturer, research direction: algebraic coding. E-mail: HPhblg@126.com
Fundation item: Supported by Research Funds of Hubei Province (D20144401 and Q20174503)
© Wuhan University 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Subsystem codes protect quantum information by encoding it in a tensor factor of a subspace of the physical state space. They generalize all major quantum error protection schemes, and therefore are exceptionally versatile.
The subsystem codes are constructions of quantum codes combining the features of decoherence-free subspaces, noiseless subsystems, and quantum error-correcting codes. These codes can potentially provide attractive features, including streamlined syndrome calculation and a diverse range of easily implementable fault-tolerant operations. An  subsystem code is a KR-dimensional subspace
subsystem code is a KR-dimensional subspace 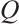 of
of 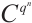 , which is decomposed into a tensor product
, which is decomposed into a tensor product 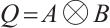 of a K-dimensional vector space
of a K-dimensional vector space 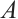 and an R-dimensional vector space
and an R-dimensional vector space  such that all errors of weight less than
such that all errors of weight less than 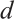 can be detected by
can be detected by 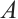 . The vector spaces
. The vector spaces 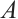 and
and 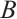 are respectively referred to as the subsystem
are respectively referred to as the subsystem 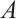 and the co-subsystem
and the co-subsystem 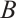 . We also use bracket notation
. We also use bracket notation 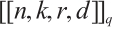 to write the parameters of an
to write the parameters of an  subsystem code in more straightforward form. For some background on subsystem codes, see the next section.
subsystem code in more straightforward form. For some background on subsystem codes, see the next section.
Aly et al[1-4] gave various methods to derive subsystem codes from classical codes over binary and non-binary fields and presented subsystem codes' families. In Ref.[5], Leng and Ma provided two methods to construct good non-binary subsystem codes. The first one is derived from quantum codes applied to non-narrow-sense BCH codes. The second one is derived from the technique of defining sets of classical cyclic codes. Recently, Qian and Zhang [6,7] constructed two new classes of subsystem maximum distance separable (MDS) codes using two classes of classical cyclic codes.
Inspired by these works, in this paper, we construct three classes of Clifford subsystem MDS codes based on linear codes, which have parameters as follows:
(i) 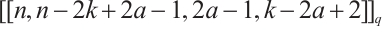 , where
, where  , and
, and 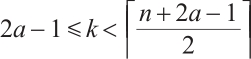 .
.
(ii) 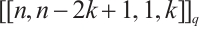 , where
, where  ,
, 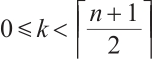 .
.
(iii) 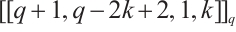 , where
, where  .
.
We conclude this introduction with a description of each section in this paper. Section 1 revisits the fundamentals and results of linear codes and subsystem codes. In Section 2 details, we construct three classes of Clifford subsystem MDS codes using Reed-Solomon codes and extended generalized Reed-Solomon codes over 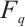 . In Section 3, we compare the Clifford subsystem codes and give a summary of this work.
. In Section 3, we compare the Clifford subsystem codes and give a summary of this work.
1 Preliminaries
In this section, we first recall some basic concepts and results about linear codes and subsystem codes necessary for the development of this work. We refer to Refs.[1, 4, 8] for more details.
Throughout this paper, let 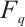 be the finite field with
be the finite field with  elements, where
elements, where 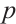 is a prime number and
is a prime number and 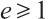 is an integer. For a positive integer
is an integer. For a positive integer 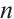 , let
, let 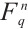 denote the vector space of all
denote the vector space of all 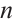 -tuples over
-tuples over 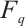 . A linear
. A linear 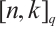 code
code  over
over 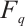 is a
is a 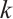 -dimensional subspace of
-dimensional subspace of  . The Hamming weight
. The Hamming weight 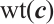 of a codeword
of a codeword  is the number of nonzero components of
is the number of nonzero components of  . The Hamming distance of two codewords
. The Hamming distance of two codewords  , is
, is  . The minimum Hamming distance
. The minimum Hamming distance 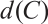 of
of 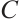 is the smallest Hamming distance between any two distinct codewords
is the smallest Hamming distance between any two distinct codewords 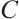 . An
. An  code is an
code is an  linear code with the minimum Hamming distance
linear code with the minimum Hamming distance 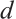 .
.
Let  . Let
. Let 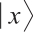 be the vectors of an orthonormal basis of
be the vectors of an orthonormal basis of 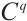 , where the labels
, where the labels 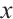 are elements of
are elements of 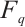 . Then
. Then 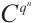 has the following orthonormal basis
has the following orthonormal basis 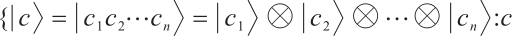
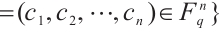 .
.
If 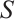 is a set, then
is a set, then  denotes the cardinality of the set
denotes the cardinality of the set  . We use the notation
. We use the notation  to denote concatenation of
to denote concatenation of 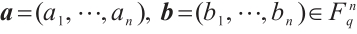 .
.
The symplectic weight of  is defined as
is defined as 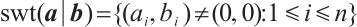 .
.
The trace-symplectic product of two vectors  and
and  in
in 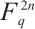 is defined as
is defined as
where  denotes the dot product and
denotes the dot product and 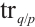 represents the trace from
represents the trace from 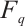 to the subfield
to the subfield 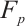 , i.e.,
, i.e., 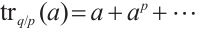
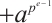 . The trace-symplectic dual of a code
. The trace-symplectic dual of a code  is defined as
is defined as  .
.
Consider  , the unitary linear operators
, the unitary linear operators  and
and 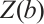 in
in  are defined by
are defined by 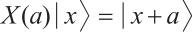 and
and 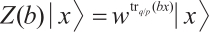 , respectively, where
, respectively, where 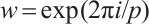 is a primitive
is a primitive 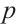 -th root of unity.
-th root of unity.
Let 
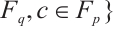 .
.
Then 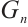 is called the error group on
is called the error group on 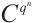 .
.
The weight of an error 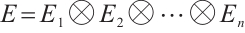 in
in 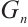 is defined as the number of
is defined as the number of 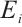 which are not equal to identity, and it is denoted by
which are not equal to identity, and it is denoted by 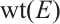 . We can also associate with
. We can also associate with  a vector
a vector 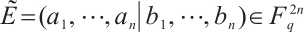 . We have
. We have
Every nontrivial normal subgroup 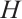 in
in 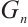 defines a subsystem code
defines a subsystem code  . Let
. Let 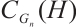 be the centralizer of
be the centralizer of 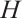 in
in 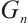 and
and 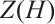 the center of
the center of 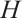 . As a subspace, the subsystem code
. As a subspace, the subsystem code 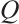 defined by
defined by  is precisely the same as the stabilizer code defined by
is precisely the same as the stabilizer code defined by 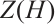 . By Ref.[9], Theorem 4,
. By Ref.[9], Theorem 4, 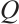 can be decomposed as
can be decomposed as  where
where 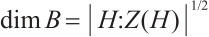 and
and
Since information is stored exclusively on subsystem 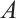 , our concern is limited to errors that affect
, our concern is limited to errors that affect  . An error
. An error 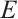 in
in 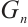 is detectable by subsystem
is detectable by subsystem 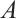 if and only if
if and only if  is contained in the set
is contained in the set  . The distance of the subsystem code
. The distance of the subsystem code 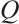 is defined as
is defined as
If 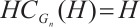 , then we define the distance of the subsystem code
, then we define the distance of the subsystem code 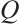 to be
to be 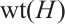 . A distance
. A distance 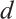 subsystem code
subsystem code 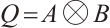 with
with 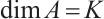 ,
,  is often denoted as
is often denoted as 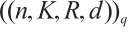 or
or 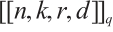 if
if 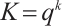 and
and 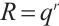 . We assert that
. We assert that 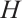 is the gauge group of
is the gauge group of  and
and 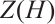 is its stabilizer. The gauge group acts trivially on
is its stabilizer. The gauge group acts trivially on 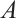 .
.
The following theorem, as presented in Ref.[1], demonstrates the relationship between subsystem codes and classical codes.
Theorem 1 Let 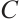 be a classical additive subcode of
be a classical additive subcode of 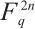 such that
such that 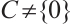 and let
and let 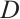 denote its subcode
denote its subcode 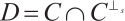 . If
. If 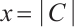 and
and 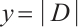 , then there exists a subsystem code
, then there exists a subsystem code  such that
such that
(1) 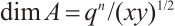 ;
;
(2)  .
.
The minimum distance of the subsystem 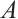 is given by
is given by
(1) 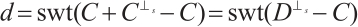 if
if 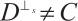 ;
;
(2)  if
if 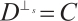 . Thus, the subsystem
. Thus, the subsystem  can detect all errors in
can detect all errors in  of weight less than
of weight less than 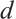 , and correct all errors in
, and correct all errors in 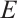 of weight
of weight 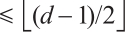 .
.
We call codes constructed using Theorem 1 as Clifford subsystem codes.
The subsequent lemma will play an essential role in constructing Clifford subsystem codes, as detailed in Ref. [2].
Theorem 2 Let 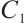 be an
be an 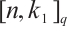 linear code such that subcode
linear code such that subcode 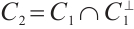 is an
is an 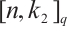 linear code and
linear code and 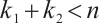 . Then there exist
. Then there exist 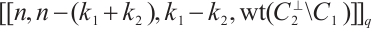 Clifford subsystem codes.
Clifford subsystem codes.
Theorem 3 (Singleton Bound for Clifford Subsystem Codes[10]) Let  be a
be a 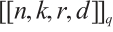 Clifford subsystem code. Then
Clifford subsystem code. Then 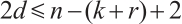 .
.
Definition 1[4] Let 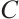 be a
be a 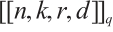 Clifford subsystem code. If
Clifford subsystem code. If 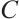 attains Singleton bound for Clifford subsystem code, i.e.,
attains Singleton bound for Clifford subsystem code, i.e., 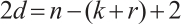 , it is termed a Clifford subsystem MDS code.
, it is termed a Clifford subsystem MDS code.
2 Constructions of Clifford Subsystem MDS Codes
In this section, we construct three classes of Clifford subsystem MDS codes employing cyclic codes and generalized Reed-Solomon codes over 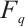 .
.
Throughout the following, we consistently assume that  is a positive integer.
is a positive integer.
A linear code of length n over  is cyclic if the code invariant under the automorphism
is cyclic if the code invariant under the automorphism 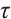 which
which
It is well-known that a cyclic code of length 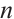 over
over  can be identified with an ideal in the residue ring
can be identified with an ideal in the residue ring 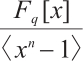 via the isomorphism
via the isomorphism 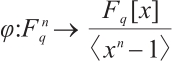 given by
given by 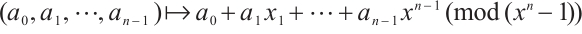 . From that, the following fact is well-known and straightforward (see Ref.[8]).
. From that, the following fact is well-known and straightforward (see Ref.[8]).
Lemma 1 If 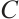 is a cyclic code of length
is a cyclic code of length 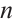 over
over  , then there exists
, then there exists  such that
such that 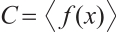 with
with 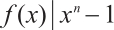 .
.
Let 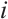 be an integer such that
be an integer such that 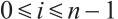 , and let
, and let 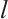 be the smallest positive integer such that
be the smallest positive integer such that  . Then
. Then 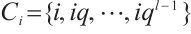 is the
is the 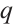 -cyclotomic coset module
-cyclotomic coset module 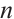 containing
containing  . Since
. Since 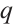 is coprime with
is coprime with  , the fundamental factors of
, the fundamental factors of 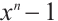 in
in 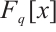 can be described by the
can be described by the 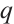 -cyclotomic cosets. Suppose that
-cyclotomic cosets. Suppose that 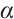 be a primitive nth root of unity over some extension field of
be a primitive nth root of unity over some extension field of 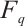 , and let
, and let  be the minimal polynomial of
be the minimal polynomial of 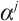 concerning
concerning  . Let
. Let 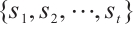 be a complete set of representatives of
be a complete set of representatives of 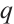 -cyclotomic cosets. Then, the polynomial
-cyclotomic cosets. Then, the polynomial 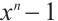 factors uniquely into monic irreducible polynomial in
factors uniquely into monic irreducible polynomial in  as
as 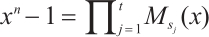 .
.
The defining set of the cyclic code 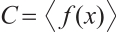 is defined as
is defined as  .
.
The defining set 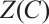 is a union of some
is a union of some 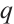 -cyclotomic co-sets and
-cyclotomic co-sets and 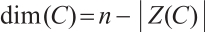 .
.
Next, we recall some primary results of generalized Reed-Solomon codes (see Ref.[7]). Let 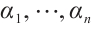 be
be 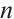 distinct elements of
distinct elements of 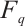 , and let
, and let  be
be 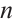 nonzero elements of
nonzero elements of 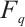 . For
. For 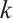 between 1 and
between 1 and 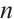 , the generalized Reed-Solomon code
, the generalized Reed-Solomon code 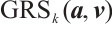 is defined by
is defined by
where 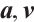 denote the vectors
denote the vectors 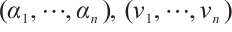 , respectively.
, respectively.
2.1 Construction 1
Let 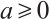 and
and 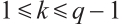 . A Reed-Solomon code (RS code) is a cyclic code of length
. A Reed-Solomon code (RS code) is a cyclic code of length 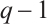 generated by
generated by
denoted by 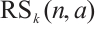 , where
, where 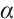 is a primitive element of
is a primitive element of 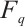 (see Ref.[11]).
(see Ref.[11]).
Remark 1 It is easy to prove that 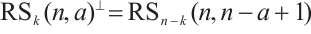 . Thus, the defining set of
. Thus, the defining set of 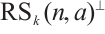 is given by
is given by 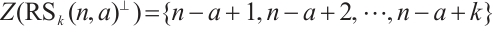 .
.
Lemma 2 Let 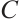 be cyclic code with defining set
be cyclic code with defining set 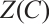 . Then the defining set of
. Then the defining set of 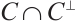 is given by
is given by  . In particular,
. In particular, 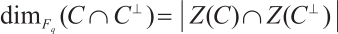 .
.
Proof According to Ref.[6] (Exercise 239, Chapter 4), we have that 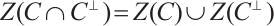 . Thus,
. Thus,
Theorem 4 Let 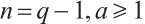 , and
, and  . Then, there is a Clifford subsystem MDS code with parameters
. Then, there is a Clifford subsystem MDS code with parameters 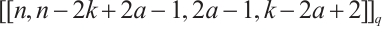 .
.
Proof Let 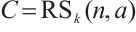 . Obviously, the defining set of
. Obviously, the defining set of 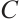 is given by
is given by 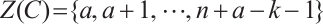 . By Remark 1, we have
. By Remark 1, we have 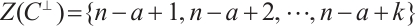 }.
}.
Since 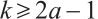 , we have
, we have 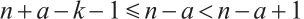 . Then, the first element in the defining set of
. Then, the first element in the defining set of 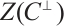 comes after the last element in
comes after the last element in  . Since
. Since  , we rewrite
, we rewrite 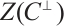 as
as 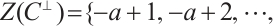
 . Then
. Then 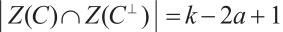 . And
. And 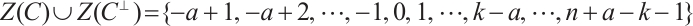 .
.
This means that 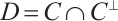 is an MDS code with parameters
is an MDS code with parameters 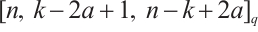 . It follows that
. It follows that 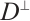 is an MDS code with parameters
is an MDS code with parameters 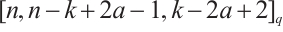 .
.
By  , we have
, we have 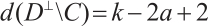 . Then, by Theorem 2, there exists a Clifford subsystem code
. Then, by Theorem 2, there exists a Clifford subsystem code 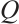 with parameters
with parameters  .
.
Since 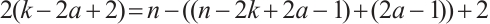 , the Clifford subsystem code
, the Clifford subsystem code 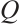 with parameters
with parameters 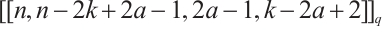 is MDS by Definition 1.
is MDS by Definition 1.
2.2 Construction 2
In this subsection, we construct a class of Clifford subsystem MDS codes by using generalized Reed-Solomon codes over  .
.
Let 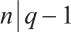 , and let
, and let 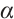 be a nth root of unity, that is
be a nth root of unity, that is  and
and  for
for 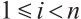 . Take
. Take 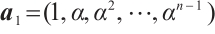 and
and 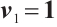 with
with 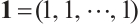 ; the generalized Reed-Solomon code
; the generalized Reed-Solomon code  have the following generator matrix:
have the following generator matrix:
where 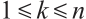 .
.
The rows of the matrix  under consideration will be denoted by
under consideration will be denoted by  .
.
Thus 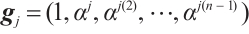 for
for 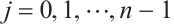 . It is easy to check that
. It is easy to check that  for
for 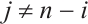 . We recall the following fact (see Ref.[12]).
. We recall the following fact (see Ref.[12]).
Lemma 3 Let  be a code generated by taking
be a code generated by taking 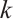 consecutive rows of the matrix
consecutive rows of the matrix 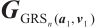 . Then
. Then  is an MDS code with parameters
is an MDS code with parameters 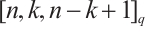 .
.
It is a routine to verify the following lemma.
Lemma 4 Let 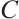 be the code with generator matrix
be the code with generator matrix 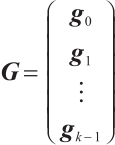 . Then
. Then 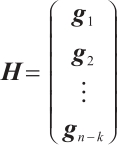 is a check matrix for
is a check matrix for 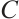 .
.
Theorem 5 Let 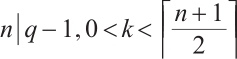 . Then, there is a Clifford subsystem MDS code
. Then, there is a Clifford subsystem MDS code 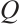 with parameters
with parameters  .
.
Proof For 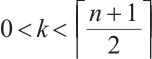 , let
, let
The code 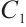 generated by the matrix
generated by the matrix  is an MDS code with parameters
is an MDS code with parameters 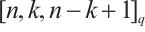 by Lemma 3. Taking
by Lemma 3. Taking 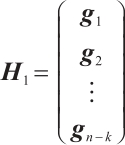 . Then, by Lemma 4,
. Then, by Lemma 4, 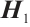 is a generator of the matrix of code
is a generator of the matrix of code  with parameters
with parameters 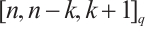 .
.
Let 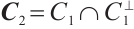 . Set
. Set 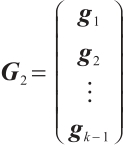 . Then, by
. Then, by  , the matrix
, the matrix 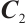 is a generator matrix for code
is a generator matrix for code 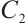 . Moreover, the code
. Moreover, the code 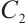 is an MDS code with parameters
is an MDS code with parameters 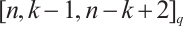 by Lemma 3. So, the code
by Lemma 3. So, the code 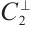 is an MDS code with parameters
is an MDS code with parameters 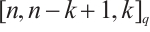 .
.
By Theorem 2, there exists a Clifford subsystem code  with parameters
with parameters 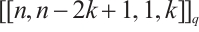 .
.
Since 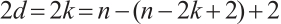 , the Clifford subsystem code
, the Clifford subsystem code 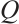 with parameters
with parameters 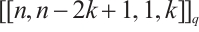 is MDS by Definition 1.
is MDS by Definition 1.
2.3 Construction 3
In this subsection, we construct a class of Clifford subsystem MDS codes by utilizing the extended code of generalized Reed-Solomon codes over 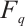 .
.
We note that the extended code of the generalized Reed-Solomon code 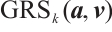 given by
given by
where 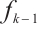 stands for the coefficient of
stands for the coefficient of 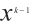 . The following two results can be found in Ref.[7].
. The following two results can be found in Ref.[7].
Lemma 5[13] The code 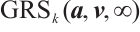 is an MDS code with parameters
is an MDS code with parameters 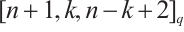 .
.
Lemma 6 [13] Let 1 be all-one word of length 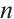 . If
. If 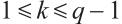 , then the dual code of
, then the dual code of 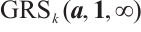 is
is 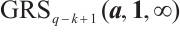 .
.
Theorem 6 Let 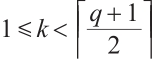 . Then, there is a Clifford subsystem MDS code with parameters
. Then, there is a Clifford subsystem MDS code with parameters 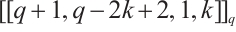 .
.
Proof Taking  . Then,
. Then, 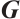 is a generator matrix of the code
is a generator matrix of the code 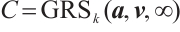 with parameters
with parameters 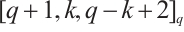 .
.
Set  . Then, by Lemma 6,
. Then, by Lemma 6,  is a parity-check matrix of the code
is a parity-check matrix of the code 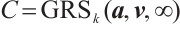 .
.
Since 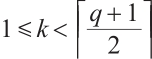 ,
,  is a generator matrix for the code
is a generator matrix for the code 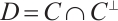 with parameters
with parameters 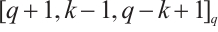 . It is easy to check that
. It is easy to check that  is a linear code with parameters
is a linear code with parameters 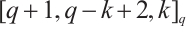 .
.
Since 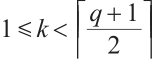 ,
, 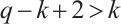 , which implies that
, which implies that  . Thus, by Theorem 2, there exists a Clifford subsystem code
. Thus, by Theorem 2, there exists a Clifford subsystem code  with parameters
with parameters 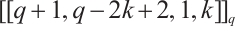 .
.
Since  , the Clifford subsystem code
, the Clifford subsystem code 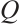 with parameters
with parameters 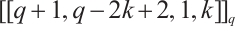 is MDS by Definition 1.
is MDS by Definition 1.
3 Comparison and Conclusion
This paper presents three new families of Clifford subsystem MDS codes employing Reed-Solomon codes and extended Reed-Solomon codes over 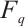 . Table 1 gives our general conclusions to compare those known results in Refs. [5-7]. The results show that the lengths of those known conclusions above Clifford subsystem codes studied in the pieces of literature are fixed or odd. However, the lengths of a class of Clifford subsystem codes derived from our construction are very flexible.
. Table 1 gives our general conclusions to compare those known results in Refs. [5-7]. The results show that the lengths of those known conclusions above Clifford subsystem codes studied in the pieces of literature are fixed or odd. However, the lengths of a class of Clifford subsystem codes derived from our construction are very flexible.
Clifford subsystem codes comparison
References
- Aly S A, Klappenecker A. Subsystem code constructions[C]//IEEE International Symposium on Information Theory. Piscaway: IEEE Press, 2008: 369-373. [Google Scholar]
- Aly S A. Asymmetric and symmetric subsystem BCH codes and beyond[EB/OL]. [2008-03-06]. https://doi.org/10.48550/arXiv.0803.0764. [Google Scholar]
- Aly S A, Ashikhmin A. Nonbinary quantum cyclic and subsystem codes over asymmetrically-decohered quantum channels[EB/OL]. [2010-07-08]. https://arxiv.org/pdf/1002.2966.pdf. [Google Scholar]
- Aly S A, Klappenecker A. Constructions of subsystem codes over finite fields[J]. International Journal of Quantum Information, 2009, 7(5): 891-912. [Google Scholar]
- Leng R, Ma Z. Constructions of new families of nonbinary asymmetric quantum BCH codes and subsystem BCH codes[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(3): 465-469. [NASA ADS] [CrossRef] [Google Scholar]
- Qian J, Zhang L. Constructions of optimal subsystem codes[J]. Modern Physics Letters B, 2012, 26(26): 501-535. [Google Scholar]
- Qian J, Zhang L. New optimal subsystem codes[J]. Discrete Mathematics, 2013, 313(21): 2451-2455. [CrossRef] [MathSciNet] [Google Scholar]
- Huffman W C, Pless V. Fundamentals of Error-Correcting Codes[M]. Cambridge: Cambridge University Press, 2003. [CrossRef] [Google Scholar]
- Klappenecker A, Sarvepalli P K. Clifford code constructions of operator quantum error-correcting codes[J]. IEEE Transactions on Information Theory, 2008, 54(12): 5760-5765. [CrossRef] [MathSciNet] [Google Scholar]
- Klappenecker A, Sarvepalli P K. On subsystem codes beating the quantum Hamming or singleton bound[J]. Mathematical, Physical and Engineering Sciences, 2007, 463(2078): 2887-2905. [Google Scholar]
- Ling S, Xing C P. Coding Theory—A First Course[M]. Cambridge: Cambridge University Press, 2004. [CrossRef] [Google Scholar]
- Hurley T, Hurley D, Hurley B. Entanglement-assisted quantum error-correcting codes from units[EB/OL]. [2018-06-28]. https://arxiv.org/pdf/1806.10875.pdf. [Google Scholar]
- Jin L, Xing C. New MDS self-dual codes from generalized Reed-Solomon codes[J]. IEEE Transactions on Information Theory, 2017, 63:1434-1438. [CrossRef] [MathSciNet] [Google Scholar]
All Tables
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.