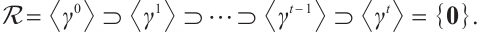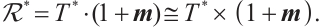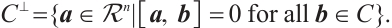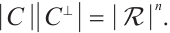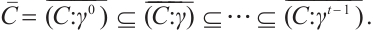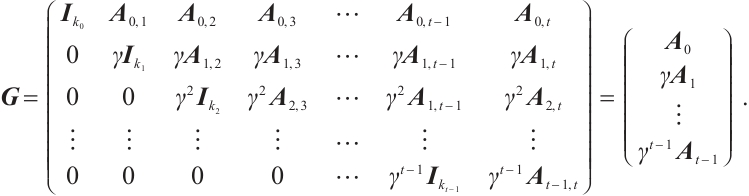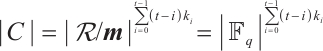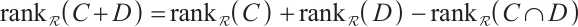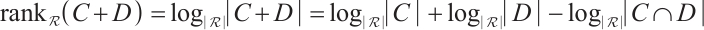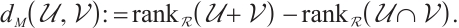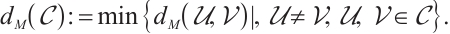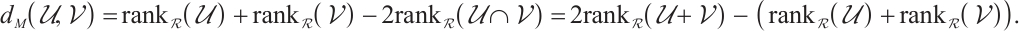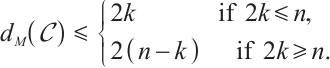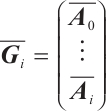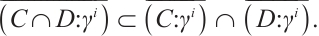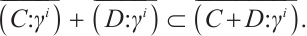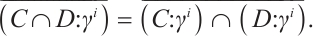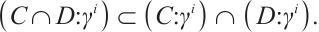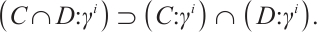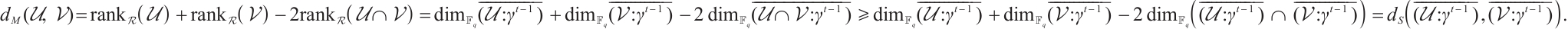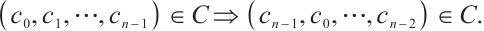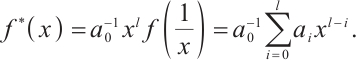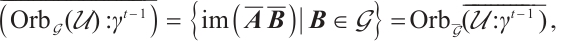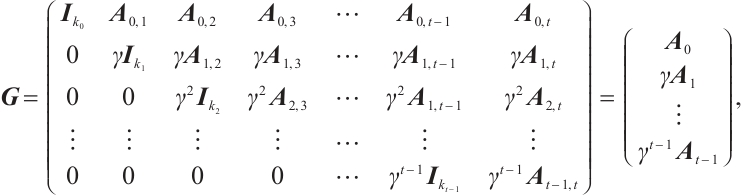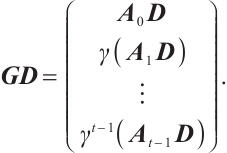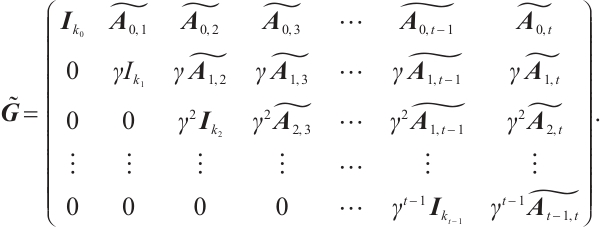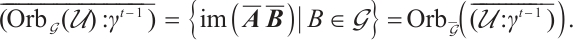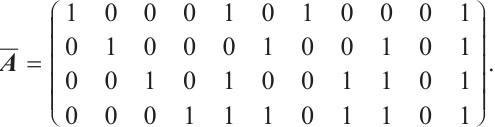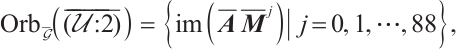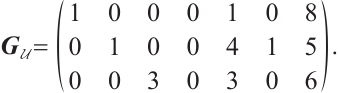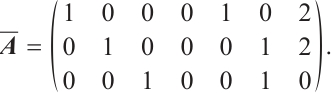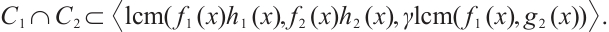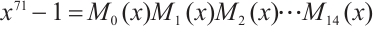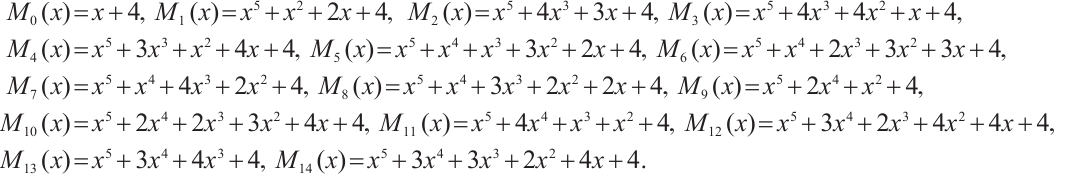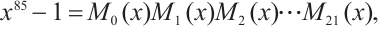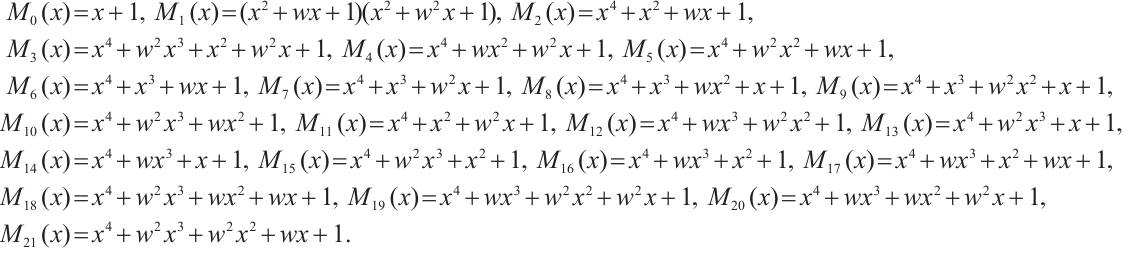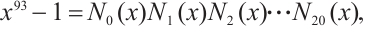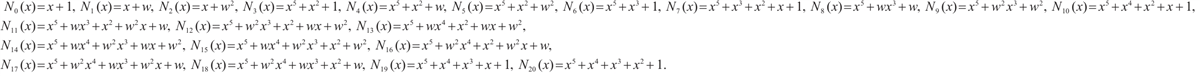| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
|
|
|---|---|---|
| Page(s) | 289 - 301 | |
| DOI | https://doi.org/10.1051/wujns/2025303289 | |
| Published online | 16 July 2025 | |
Mathematics
CLC number: O236.2
Construction of Constant Rank and Orbit Codes over Finite Chain Rings
有限链环上常秩和轨道码的构造
Department of Science and Technology, College of Arts and Science of Hubei Normal University, Huangshi 435109, Hubei, China
† Corresponding author. E-mail: lxs6682@163.com
Received:
3
November
2024
In this paper, we first generalize the constant dimension and orbit codes over finite fields to the constant rank and orbit codes over finite chain rings. Then we provide a relationship between constant rank codes over finite chain rings and constant dimension codes over the residue fields. In particular, we prove that an orbit submodule code over a finite chain ring is a constant rank code. Finally, for special finite chain ring 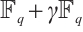 , we define a Gray map
, we define a Gray map 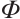 from
from 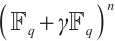 to
to 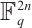 , and by using cyclic codes over
, and by using cyclic codes over 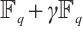 , we obtain a method of constructing an optimum distance constant dimension code over
, we obtain a method of constructing an optimum distance constant dimension code over 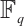 .
.
摘要
本文将有限域上常维数和轨道码推广到有限链环上的常秩和轨道码。我们提供了有限链环的常秩码和它的剩余类域的常维数码之间的一种关系。特别地,证明了有限链环上的轨道子模码是一个常秩码。最后,对于特殊有限链环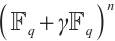 ,定义了一个Gray映射从
,定义了一个Gray映射从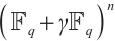 到
到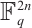 的Gray映射
的Gray映射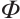 ,借助
,借助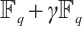 上的循环码,得到域
上的循环码,得到域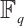 上一种构造极优距离常维数码的办法。
上一种构造极优距离常维数码的办法。
Key words: finite chain ring / rank of linear codes / constant rank codes / orbit codes
关键字 : 有限链环 / 线性码的秩 / 常秩码 / 轨道码
Cite this article: GUO Ye, LIU Xiusheng. Construction of Constant Rank and Orbit Codes over Finite Chain Rings[J]. Wuhan Univ J of Nat Sci, 2025, 30(3): 289-301.
Biography: GUO Ye, male, Master, Lecturer, research direction: algebraic coding. E-mail: 771088974@qq.com
Foundation item: Supported by Research Funds of Hubei Province (D20144401, Q20174503)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Random linear network coding, first introduced in Ref. [1], is a strong tool for effective data transmission over noisy and lossy networks. It was proved in Ref. [1] that the information rate of a network can be improved by using coding at the nodes of the network, instead of simply routing the received inputs. An algebraic approach to random network coding was provided by Koetter and Kschischang in Ref. [2]. They proposed transmitting information by means of the subspaces of finite fields 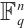 and defined subspace codes as a class of codes well suited for error correction. In the case that all the codewords in a subspace code have the same dimension, the subspace code is said to be a constant dimension subspace code. The theory of constant dimension subspace code has received a lot of attention in recent years (see Refs. [3-9]). As we know, the approach of constructing good constant dimension subspace codes is an interesting research field. In Ref. [9], Trautmann et al introduced the concept of orbit codes as subspace codes obtained from the action of subgroups of the general linear group
and defined subspace codes as a class of codes well suited for error correction. In the case that all the codewords in a subspace code have the same dimension, the subspace code is said to be a constant dimension subspace code. The theory of constant dimension subspace code has received a lot of attention in recent years (see Refs. [3-9]). As we know, the approach of constructing good constant dimension subspace codes is an interesting research field. In Ref. [9], Trautmann et al introduced the concept of orbit codes as subspace codes obtained from the action of subgroups of the general linear group 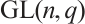 on the set of subspaces of
on the set of subspaces of 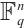 . When the acting group is cyclic, the code is called a cyclic orbit code. Because of the simplicity of their algebraic structure and the existence of efficient encoding/decoding algorithms, this family of codes has attracted great interest. Gluesing-Luerssen and Lehmann[3] presented a detailed study of cyclic orbit codes based on the stabilizer subfield. Later, Gluesing-Luerssen et al[4] investigated the structure of the distance distribution for cyclic orbit codes, which are subspace codes generated by the action of
. When the acting group is cyclic, the code is called a cyclic orbit code. Because of the simplicity of their algebraic structure and the existence of efficient encoding/decoding algorithms, this family of codes has attracted great interest. Gluesing-Luerssen and Lehmann[3] presented a detailed study of cyclic orbit codes based on the stabilizer subfield. Later, Gluesing-Luerssen et al[4] investigated the structure of the distance distribution for cyclic orbit codes, which are subspace codes generated by the action of 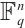 on an
on an 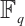 -subspace
-subspace 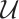 of
of 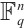 . Ref. [10] gave a systematic construction of subspace codes using subspace polynomials. By using Ben-Sasson’s idea, Chen et al[6] also provided some constructions of cyclic subspace codes. Roth et al[11] and Zhang et al[12] generalized and improved their result, so that one can obtain larger codes for fixed parameters and increase the density of some possible parameters.
. Ref. [10] gave a systematic construction of subspace codes using subspace polynomials. By using Ben-Sasson’s idea, Chen et al[6] also provided some constructions of cyclic subspace codes. Roth et al[11] and Zhang et al[12] generalized and improved their result, so that one can obtain larger codes for fixed parameters and increase the density of some possible parameters.
Linear codes over finite rings have played a very important role in the theory of error correcting codes and practice (see Refs. [13-19]). On the one hand, by means of linear codes over finite rings, one can obtain good linear codes over finite fields (see Refs. [20-22]). On the other hand, new quantum codes and entanglement-assisted quantum codes can be obtained from linear codes over finite rings (see Refs. [23-27]).
Inspired by these works, in this paper, we first generalize subspace codes over finite fields to submodule codes over finite chain rings, and generalize constant dimension codes over finite fields to constant rank codes over finite chain rings. Under suitable conditions, we give a characterization of the constant rank codes over finite chain rings. We give a sufficient condition for which an orbit submodule code over a finite chain ring is a constant rank code.
This paper is organized as follows. In Section 1, we recall the necessary background materials of linear codes over finite chain rings. In Section 2, we first generalize the constant dimension codes over finite fields to constant rank codes over finite chain rings. Then, we give a relationship between constant rank codes over finite chain rings and constant dimension codes over the residue fields. By means of this relationship, we obtain a method to construct constant rank codes over finite chain rings. In Section 3, we collect concepts of orbit codes over finite fields, which are generalized to the orbit submodule codes over finite chain rings. Then we study orbit submodule constant rank codes over finite chain rings. We give two new examples of the open problem proposed by Gluesing-Luerssen et al in Ref. [4] (see Examples 1 and 2). In Section 4, we define a Gray map 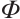 from
from 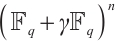 to
to 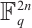 , and we give a method for constructing an optimum distance constant dimension code over
, and we give a method for constructing an optimum distance constant dimension code over 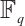 by using cyclic codes over
by using cyclic codes over  . Finally, a brief summary of this work is described in Section 5.
. Finally, a brief summary of this work is described in Section 5.
1 Linear Codes over Chain Rings
Throughout this paper 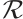 will denote a finite chain ring. In this section, we recall some basic concepts and results of linear codes over
will denote a finite chain ring. In this section, we recall some basic concepts and results of linear codes over  , necessary for the development of this work. For more details, we refer to Refs. [16, 19, 28-30].
, necessary for the development of this work. For more details, we refer to Refs. [16, 19, 28-30].
It is well known that  has the unique maximal ideal, denoted by
has the unique maximal ideal, denoted by  . Let
. Let  be a generator of the unique maximal ideal
be a generator of the unique maximal ideal  , i.e.,
, i.e., 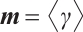 . Its chain of ideals is
. Its chain of ideals is
The integer 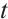 is called the nilpotency index of
is called the nilpotency index of  . Let
. Let 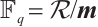 be the residue field with characteristic
be the residue field with characteristic 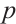 , where
, where 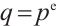 and
and 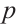 is a prime number. There is a natural homomorphism from
is a prime number. There is a natural homomorphism from 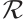 onto
onto 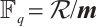 , i.e.,
, i.e.,
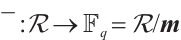 ,
,  , for any
, for any 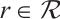 .
.
This natural homomorphism from 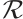 onto
onto 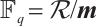 can be extended naturally to a homomorphism from
can be extended naturally to a homomorphism from 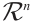 onto
onto 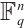 . For an element
. For an element  , let
, let 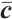 be its image under this homomorphism.
be its image under this homomorphism.
Let  denote the group of units of
denote the group of units of 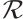 .
. 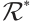 is just the set of non-nilpotent elements of
is just the set of non-nilpotent elements of 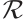 i.e.,
i.e., 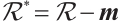 . The subgroup
. The subgroup 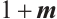 of
of 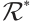 is a
is a 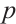 -group.
-group.
It is well known that the group of units 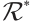 of
of 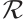 contains a unique cyclic subgroup
contains a unique cyclic subgroup 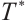 of order
of order 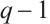 .
. 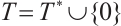 is called the Teichmüller set of
is called the Teichmüller set of 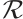 and forms a system of coset representatives of
and forms a system of coset representatives of 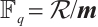 . More precisely,
. More precisely, 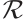 contains a unit element
contains a unit element 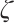 with multiplicative order
with multiplicative order 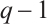 such that
such that 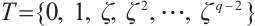 . We call
. We call 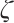 the generator of
the generator of 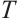 . Since the set
. Since the set 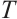 modulo
modulo 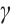 equals
equals 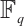 , we do not make distinction between
, we do not make distinction between 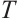 and
and 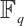 . Every element
. Every element 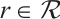 can be written as
can be written as 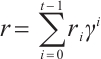 , where
, where 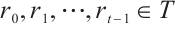 (see Refs. [7,18]).
(see Refs. [7,18]).
Lemma 1 Let notations be as above. We have
A nonempty subset  is called a linear code of length
is called a linear code of length 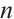 over
over 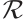 if it is an
if it is an 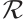 -submodule of
-submodule of 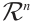 . All codes are assumed to be linear. We say that a linear code
. All codes are assumed to be linear. We say that a linear code 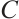 over
over 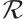 is free if
is free if 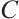 is isomorphic as a module to
is isomorphic as a module to 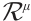 for some positive lnteger
for some positive lnteger 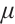 , denoted by
, denoted by 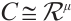 .
.
For two vectors 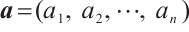 and
and 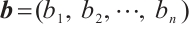 in
in 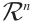 , we define the Euclidean inner product as
, we define the Euclidean inner product as 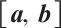 to be
to be 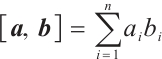 .
.
Let 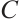 be a linear code over
be a linear code over 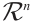 . We define the Euclidean dual code of
. We define the Euclidean dual code of 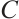 as
as
The following lemma is well-known in Ref. [30].
Lemma 2 Let 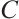 be a linear code of length
be a linear code of length 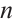 over
over 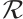 (or an
(or an 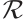 -submodule of
-submodule of 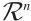 ). Then
). Then
One of the most important tools in coding theory is finding a generator matrix for a code. In general, we want not only a matrix that generates code by rows, but also a matrix that generates code by a minimum number of rows. To describe the generator matrix for a code over 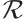 , we introduce the following two definitions and lemmas which come from Refs. [16, 28].
, we introduce the following two definitions and lemmas which come from Refs. [16, 28].
Definition 1 Let  be nonzero vectors in
be nonzero vectors in 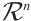 . Then
. Then  are
are 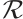 -independent if
-independent if 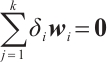 implies that
implies that 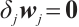 for all
for all 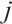 , where
, where 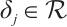 .
.
Following Definition 1, we can easily get the following lemma.
Lemma 3 If the nonzero vectors 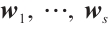 in
in 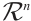 are
are 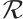 -independent and
-independent and 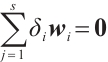 , then
, then 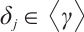 for all
for all 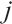 .
.
Let 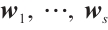 be vectors in
be vectors in 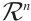 . As usual, we denote the set of all linear combinations of
. As usual, we denote the set of all linear combinations of 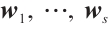 by
by  .
.
Lemma 4 If the nonzero vectors 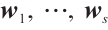 in
in 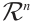 are
are 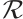 -independent, then none of the vectors
-independent, then none of the vectors 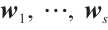 is a linear combination of the other vectors.
is a linear combination of the other vectors.
With the help of the above definition and two lemmas, we give a definition of a generator matrix for a code over 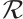 .
.
Definition 2 Let 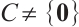 be a linear code over
be a linear code over 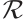 (or an
(or an 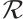 -submodule of
-submodule of  ). The nonzero codewords
). The nonzero codewords 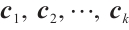 are called a basis of
are called a basis of 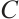 if they are
if they are 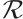 -independent and generate
-independent and generate 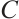 . Let
. Let 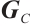 be a
be a  matrix where
matrix where  are rows of
are rows of 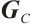 . Then
. Then 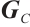 is a generator matrix of
is a generator matrix of 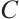 .
.
Definition 3 A parity-check matrix 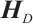 for a linear code
for a linear code 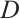 over
over 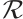 is a generator matrix for the dual code
is a generator matrix for the dual code 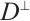 .
.
Let 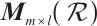 be the set of all
be the set of all  matrices over
matrices over 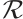 . For
. For 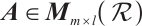 ,
, 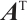 denotes the transpose of the matrix
denotes the transpose of the matrix 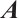 . We also let
. We also let 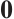 denote the zero matrix, where the size will either be obvious from the context or specified whenever necessary. Similarly, we denote the
denote the zero matrix, where the size will either be obvious from the context or specified whenever necessary. Similarly, we denote the  identity matrix by
identity matrix by 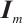 , or simply
, or simply  if the size is clear from the context.
if the size is clear from the context.
Let 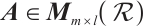 , and let
, and let  and
and  be the submodules generated by the rows of
be the submodules generated by the rows of 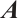 and the columns of
and the columns of 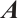 , respectively. Now, we introduce the definition of the row-rank (or column-rank) of the matrix from Ref. [31].
, respectively. Now, we introduce the definition of the row-rank (or column-rank) of the matrix from Ref. [31].
Definition 4 The parameter 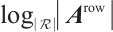 is called the row-rank of the matrix
is called the row-rank of the matrix 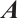 and denoted by
and denoted by 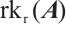 , and similarly
, and similarly 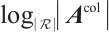 is called the column-rank of the matrix
is called the column-rank of the matrix 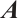 and denoted by
and denoted by 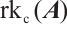 .
.
Obviously, when 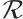 is a finite field, the above definition coincides with the usual rank of a matrix. We need the following two lemmas which can be found in Ref. [31].
is a finite field, the above definition coincides with the usual rank of a matrix. We need the following two lemmas which can be found in Ref. [31].
Lemma 5 Let 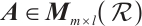 . Then
. Then 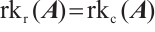 .
.
In 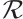 , we define
, we define 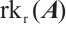 or
or 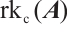 as the rank of the matrix
as the rank of the matrix 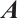 , denoted by
, denoted by 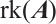 . The following two concepts and a result about matrices over finite chain rings appear in Ref. [32].
. The following two concepts and a result about matrices over finite chain rings appear in Ref. [32].
Let 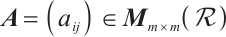 . If there is an
. If there is an  matrix
matrix 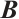 over
over 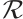 such that
such that 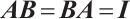 , then
, then 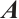 is invertible and
is invertible and 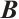 is an inverse of
is an inverse of 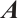 . If the determinant
. If the determinant 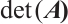 is a unit of
is a unit of  , then
, then  is non-singular.
is non-singular.
Lemma 6 Let  be an
be an  matrix over
matrix over 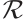 . The following statements are equivalent: (1)
. The following statements are equivalent: (1) 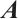 is invertible; (2)
is invertible; (2) 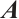 is non-singular; (3)
is non-singular; (3) 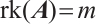 .
.
Lemma 7 Let 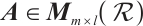 and
and 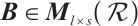 . Then
. Then 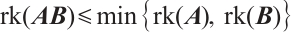 .
.
Corollary 1 Let 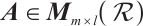 . If
. If 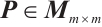 and
and 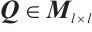 are non-singular, then
are non-singular, then 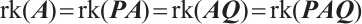 .
.
Proof Let 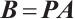 . Then, by Lemma 7, we have
. Then, by Lemma 7, we have 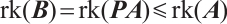 . On the other hand, considering the matrix
. On the other hand, considering the matrix 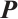 is non-singular, we obtain
is non-singular, we obtain 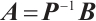 . Again by Lemma 7, we have
. Again by Lemma 7, we have 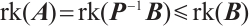 . Therefore,
. Therefore, 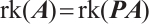 .
.
Similarly, we can show that 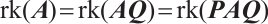 .
.
Definition 5 Let 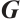 be a generator matrix of a linear code
be a generator matrix of a linear code 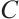 over
over 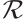 . Then the rank of the code
. Then the rank of the code 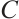 , denoted by
, denoted by 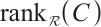 , is defined as
, is defined as 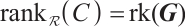 .
.
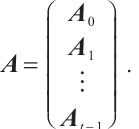
Let 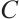 be a code of length
be a code of length 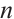 over
over 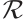 . We define
. We define 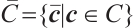 and
and 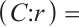
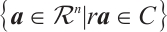 , where
, where 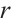 is an element of
is an element of 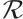 . The following two definitions can be found in Ref. [22].
. The following two definitions can be found in Ref. [22].
Definition 6 To any code 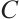 over
over 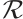 , we associate the tower of codes
, we associate the tower of codes 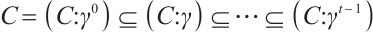 over
over 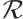 and its projection to
and its projection to 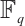 ,
,
Definition 7 Let 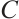 be a linear code over
be a linear code over 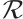 . A generator matrix
. A generator matrix 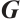 for
for 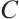 is said to be in standard form if, after a suitable permutation of the coordinates,
is said to be in standard form if, after a suitable permutation of the coordinates, 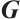 can be written as the following block matrix:
can be written as the following block matrix:
We associate the following matrix with 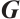
For any constant 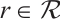 and any
and any  , we denote by
, we denote by 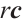 the usual multiplication of a vector by a scalar. We say that a vector
the usual multiplication of a vector by a scalar. We say that a vector  is divisible by a constant
is divisible by a constant 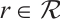 , and write as
, and write as 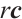 , if there exists a vector
, if there exists a vector 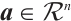 such that
such that 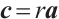 , i.e., all entries of
, i.e., all entries of 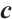 are divisible by
are divisible by 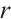 .
.
Let 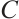 be a linear code over
be a linear code over 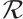 . For
. For  we denote by
we denote by 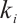 the number of row vectors of
the number of row vectors of 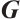 that are divisible by
that are divisible by 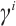 but not by
but not by 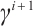 . A code with generator matrix of this form is said to have type
. A code with generator matrix of this form is said to have type 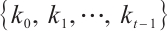 . It is immediate that the number of elements in a code
. It is immediate that the number of elements in a code 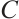 with this generator matrix is
with this generator matrix is
Thus, we have 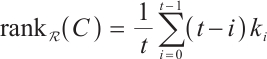 . This means that the rank of a linear code over
. This means that the rank of a linear code over 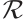 could be a fraction.
could be a fraction.
2 Constant Rank Codes over Chain Rings
In this section, we first generalize the constant dimension and orbit codes over finite fields to the constant rank and orbit codes over finite chain rings. Then, a method of constructing the constant rank code over 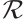 is given.
is given.
In order to give the definition of the rank distance of a submodule code over finite chain rings, we need the following lemma.
Lemma 8 Let 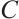 and
and 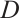 be two linear codes of length
be two linear codes of length 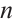 over
over 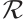 . Then we have
. Then we have
Proof Let 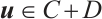 . Then there are
. Then there are 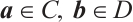 such that
such that 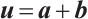 . Obviously, for any
. Obviously, for any 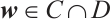 , we have
, we have
Thus, there are 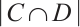 such expressions for
such expressions for 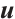 . This means that
. This means that 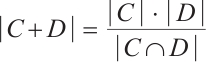 . So,
. So,
i.e., 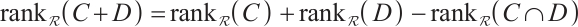 .
.
Definition 8 Let 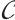 be a set of submodules (or linear codes) of length
be a set of submodules (or linear codes) of length 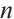 over
over 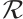 . Then
. Then  is called a submodule code of length
is called a submodule code of length 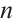 over
over 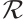 . The submodule code
. The submodule code 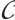 is called a constant rank code if all submodules have the same rank. If every submodule of
is called a constant rank code if all submodules have the same rank. If every submodule of 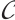 has the same type
has the same type 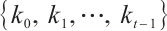 , then the submodule code
, then the submodule code 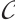 is called a constant rank code of type
is called a constant rank code of type 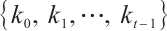 .
.
Definition 9 Let 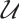 and
and 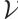 be two submodules over
be two submodules over 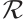 . Then the rank distance is defined as
. Then the rank distance is defined as
The minimum rank distance of a submodule code 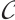 is definite as
is definite as
Remark 1 By Lemma 8, we have
As a consequence, suppose that 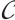 is a constant rank code of rank
is a constant rank code of rank 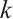 and length
and length 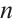 , then its minimum submodule distance is even integer and it is upper bounded by
, then its minimum submodule distance is even integer and it is upper bounded by
This bound is attained by submodule code in which the intersection of every two different submodules has rank of max{0, 2k n} .
n} .
Remark 2 When 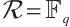 , the submodule code
, the submodule code 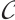 is a subspace code. In this case, the distance between two subspace is
is a subspace code. In this case, the distance between two subspace is 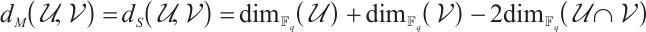 . This means that the distance of subspace code over
. This means that the distance of subspace code over 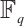 is a special case of the rank distance of submodule code over
is a special case of the rank distance of submodule code over 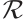 .
.
Let 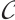 be a constant rank code of rank
be a constant rank code of rank 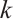 and length
and length 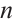 over
over 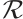 . If it attains bound
. If it attains bound 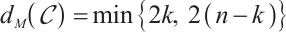 , then
, then 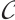 is called an optimum distance constant rank code.
is called an optimum distance constant rank code.
A code 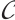 is called an
is called an 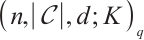 submodule code over
submodule code over 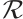 if the ranks of the codewords of
if the ranks of the codewords of 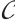 are contained in a set
are contained in a set 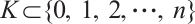 . In the case
. In the case 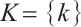 , i.e.,
, i.e., 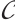 is a constant rank code, we denote its parameters by
is a constant rank code, we denote its parameters by 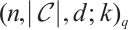 , where
, where 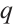 is the number of elements of the residue field
is the number of elements of the residue field 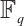 . If all codewords do not have the same rank, then
. If all codewords do not have the same rank, then 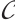 is called a mixed rank code. Such submodule code is denoted by
is called a mixed rank code. Such submodule code is denoted by 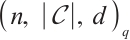 . Constant rank codes are the most well-studied submodule codes, being the analogues of classical codes over finite rings.
. Constant rank codes are the most well-studied submodule codes, being the analogues of classical codes over finite rings.
Remark 3 When 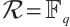 , the submodule code
, the submodule code  is a subspace code. In this case, the distance between two subspace is
is a subspace code. In this case, the distance between two subspace is 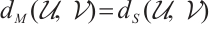 . This means that the parameters of submodule codes over
. This means that the parameters of submodule codes over 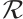 are generalizations of the parameters of subspace codes over
are generalizations of the parameters of subspace codes over 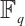 .
.
In order to connect a constant rank code of rank 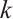 and length
and length 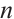 over
over 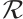 with a constant dimension code of dimension
with a constant dimension code of dimension 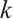 and length
and length 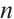 over
over 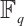 , we need the following lemma, which can be found in Ref. [19].
, we need the following lemma, which can be found in Ref. [19].
Lemma 9 (Lemma 9 in Ref. [19]) Suppose that C is a linear code of length 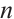 over
over 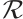 with a generator matrix
with a generator matrix 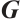 in standard form (1) and let
in standard form (1) and let 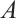 be as in
be as in 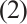 . Then, for
. Then, for 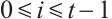 ,
, 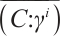 has a generator matrix
has a generator matrix
In addition, 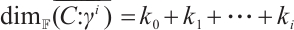 .
.
Lemma 10 Let 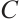 and
and 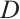 be two linear codes over
be two linear codes over 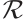 . Then, for
. Then, for 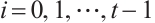 , we have
, we have
Proof 1) We first prove that
In fact, for any 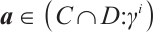 , we have
, we have 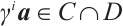 . So,
. So, 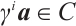 and
and 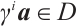 , which implies that
, which implies that 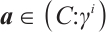 and
and  . Thus,
. Thus, 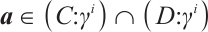 , i. e.,
, i. e.,
On the other hand, let 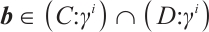 . Then
. Then 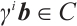 and
and 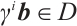 . This means that
. This means that 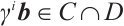 ,i. e.,
,i. e., 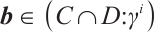 . Thus,
. Thus,
Combining Eqs. (6) and (7), we have 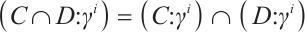 . So, the Eq. (5) holds.
. So, the Eq. (5) holds.
Next, let 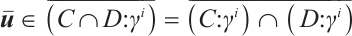 , where
, where 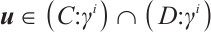 . Then
. Then 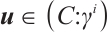 and
and  . Therefore,
. Therefore, 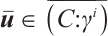 and
and 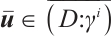 , which implies that
, which implies that 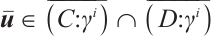 . Thus, we complete the proof of Eq. (3).
. Thus, we complete the proof of Eq. (3).
2) For any 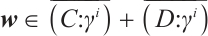 , there are
, there are 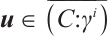 and
and 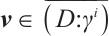 such that
such that 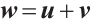 . Thus, we can find that
. Thus, we can find that 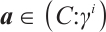 and
and 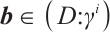 with
with 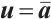 and
and 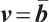 . This means that
. This means that 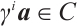 and
and 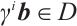 . Therefore,
. Therefore, 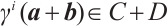 , i.e.,
, i.e., 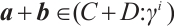 . Hence,
. Hence, 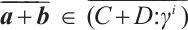 . Since
. Since  is a homomorphism from
is a homomorphism from 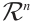 onto
onto 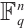 , we have
, we have 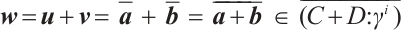 . This prove that
. This prove that 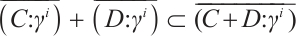 , i.e., we complete the proof of Eq. (4).
, i.e., we complete the proof of Eq. (4).
Let 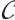 be submodule code of length
be submodule code of length 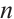 over
over 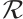 . In the following, we denote by
. In the following, we denote by 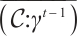 the set
the set 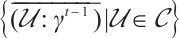 .
.
Combining Lemmas 9 and 10, we give the following theorem.
Theorem 1 Let 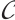 be a submodule code of length
be a submodule code of length 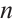 over
over 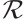 with type
with type 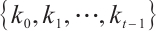 and the minimum rank distance
and the minimum rank distance 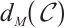 . Then
. Then
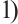
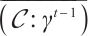 is a constant dimension code over
is a constant dimension code over 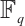 of dimension
of dimension 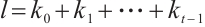 and length
and length 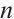 . In addition,
. In addition,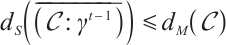 .
.
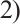 In particular, write
In particular, write 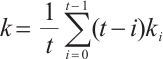 . If
. If 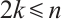 and
and 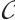 is an optimum distance constant rank code, then
is an optimum distance constant rank code, then 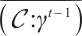 is also an optimum distance constant dimension code with the minimum distance
is also an optimum distance constant dimension code with the minimum distance 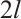 .
.
Proof 1) By assumptions, for any 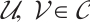 , we have
, we have 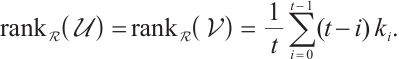
According to Lemma 9, for any 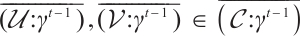 , we obtain
, we obtain 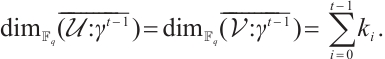
Thus, 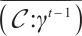 is a constant dimension code over
is a constant dimension code over 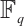 of dimension
of dimension 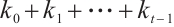 and length
and length 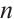 .
.
On the other hand, by Lemmas 9 and 10, for any 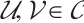 , we obtain
, we obtain
This gives that 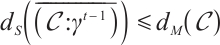 .
.
2) In particular, if 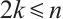 and
and 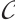 is an optimum distance constant rank code, for any
is an optimum distance constant rank code, for any 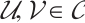 , we have
, we have 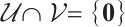 .
.
Let 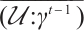 and
and 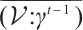 be any two different elements of
be any two different elements of 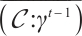 . We prove that
. We prove that 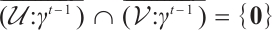 by contradiction as follows.
by contradiction as follows.
Otherwise, there exists 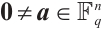 such that
such that 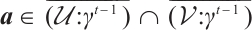 . Hence, we can find that
. Hence, we can find that 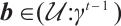 and
and 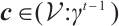 satisfy
satisfy 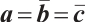 .
.
We assume that 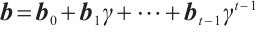 and
and 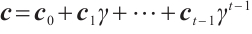 with
with 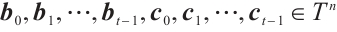 , where
, where 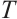 is the
is the 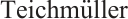 set of
set of 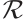 . Then, by
. Then, by 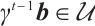 and
and 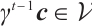 , we have
, we have 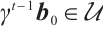 and
and 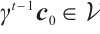 . Thus, we obtain
. Thus, we obtain 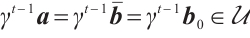 , and
, and 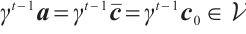 . This gives that
. This gives that 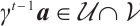 . Obviously,
. Obviously, 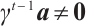 . This is a contradiction. Thus, for any
. This is a contradiction. Thus, for any 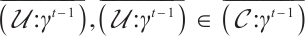 , we have
, we have 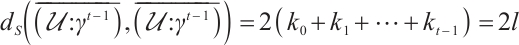 , which implies that
, which implies that 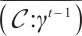 is an optimum distance constant dimension code with the minimum distance
is an optimum distance constant dimension code with the minimum distance 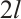 .
.
A linear code 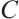 over
over 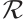 of length
of length 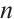 is said to be cyclic if the following holds:
is said to be cyclic if the following holds:
It is well-known that a cyclic code of length 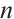 over
over  can be identified with an ideal in the residue ring
can be identified with an ideal in the residue ring 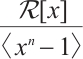 via the
via the 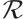 -module isomorphism
-module isomorphism 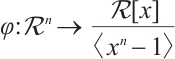 given by
given by 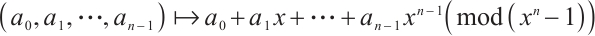 .
.
Customarily, for a polynomial 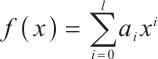 of degree
of degree 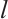 (
(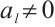 and
and 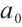 is a unit) over
is a unit) over 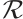 , its monic reciprocal polynomial
, its monic reciprocal polynomial 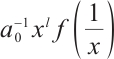 is denoted by
is denoted by 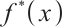 , i.e.,
, i.e.,
A polynomial 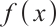 is self-reciprocal, if
is self-reciprocal, if 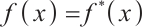 .
.
The homomorphism from 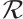 to
to 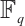 extends naturally to a homomorphism
extends naturally to a homomorphism 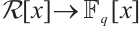 , where
, where 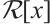 and
and 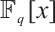 are the corresponding polynomial rings; for any
are the corresponding polynomial rings; for any 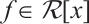 we denote by
we denote by 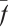 its image under this homomorphism; moreover, for a set
its image under this homomorphism; moreover, for a set 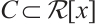 we define
we define 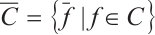 .
.
It is well known that any 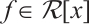 which is not divisible by
which is not divisible by 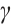 can be written as
can be written as 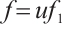 , where
, where 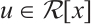 is a unit and
is a unit and 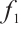 is monic. We will therefore restrict our attention to monic polynomials.
is monic. We will therefore restrict our attention to monic polynomials.
The following is basic result of cyclic codes over 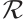 .
.
Theorem 2 (Theorem 4.5 in Ref. [19]) Let 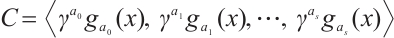 be a cyclic code of length
be a cyclic code of length 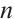 over
over 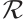 , where
, where 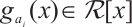 are monic. Then
are monic. Then
1) 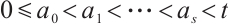 , and
, and 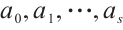 are unique.
are unique.
2) 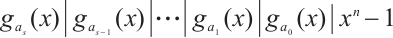 ,
, 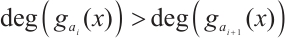 for
for  , and
, and 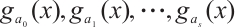 are unique.
are unique.
3) If 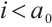 , then
, then 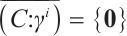 , otherwise
, otherwise 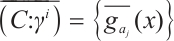 , where
, where 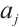 is maximal with the property
is maximal with the property 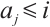 .
.
4) 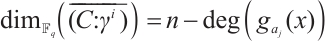 , where
, where 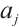 is maximal with the property
is maximal with the property 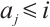 .
.
Combining Theorems 1 and 2, we obtain the following corollary.
Corollary 2 For 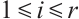 , let
, let 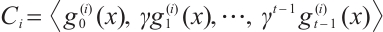 be a cyclic code of length
be a cyclic code of length 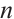 over
over 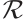 , where
, where 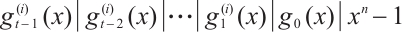 , and
, and 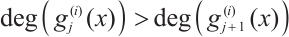 for
for  . Let
. Let 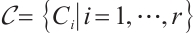 . If
. If  for
for 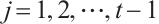 , then
, then 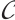 is a constant rank code over
is a constant rank code over 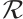 of rank
of rank 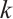 and length
and length 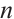 , where
, where 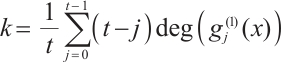 .
.
3 Orbit Constant Rank Codes over Finite Chain Rings
From now on, we denote by 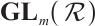 the set
the set 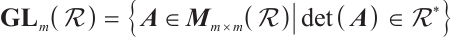 . It is well known that
. It is well known that 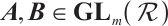 if and only if
if and only if 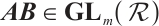 .
.
Let  be a linear (submodule) code of length
be a linear (submodule) code of length  over
over  with a generator matrix
with a generator matrix 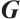 in standard form in (1). Clearly,
in standard form in (1). Clearly, 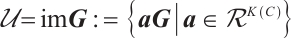 , i.e., the submodule of
, i.e., the submodule of 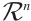 generated by the rows of
generated by the rows of 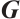 .
.
Definition 10 Let 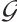 be a subgroup of
be a subgroup of 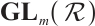 ,
, 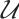 be a linear code (submodule) of length
be a linear code (submodule) of length 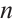 over
over 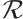 with a generator matrix
with a generator matrix 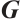 in standard form in (1). The orbit submodule code generated by
in standard form in (1). The orbit submodule code generated by 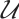 with respect to the subgroup
with respect to the subgroup 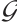 , denoted by
, denoted by 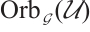 , is defined as
, is defined as 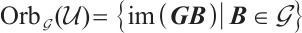 .
.
Theorem 3 Let  be a subgroup of
be a subgroup of  , and
, and 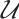 be a linear code (submodule) of length
be a linear code (submodule) of length 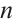 over
over 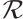 with a generator matrix
with a generator matrix 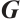 in standard form in (1). Set
in standard form in (1). Set 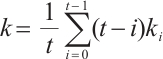 . Then orbit submodule code
. Then orbit submodule code 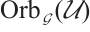 is a constant rank code over
is a constant rank code over 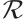 of rank
of rank 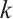 , length
, length 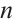 . In particular, take
. In particular, take 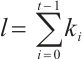 , then
, then 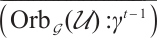 is a constant dimension code over
is a constant dimension code over 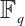 of dimension
of dimension 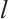 , length
, length 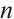 , and
, and 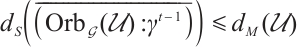 . Moreover,
. Moreover,
where 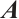 is in (2), and
is in (2), and 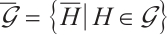 .
.
Proof For any 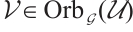 , there exists
, there exists 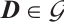 such that
such that 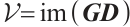 . Since
. Since
we have that 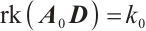 ,
, 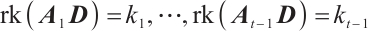 by Corollary 1.
by Corollary 1.
On the other hand, we have
Clearly, after a suitable permutation of coordinates, we obtain a generator matrix 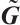 in standard form of the submodule
in standard form of the submodule 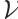 as follows
as follows
Thus, 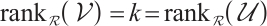 . This means that orbit submodule code
. This means that orbit submodule code 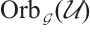 is a constant rank code over
is a constant rank code over 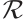 of rank
of rank 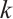 , length
, length 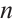 .
.
The second statement follows directly from Theorem 1.
By Lemma 9, 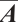 is a generator matrix of the linear code
is a generator matrix of the linear code 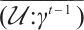 over
over 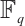 .
.
For any 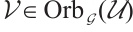 , by Definition 10, there is a
, by Definition 10, there is a 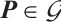 such that
such that 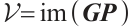 . Then
. Then  is a generator matrix of the linear code
is a generator matrix of the linear code 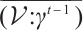 over
over 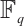 . This means that
. This means that
In the following, we give two examples to demonstrate Theorem 3. We use the Magma Computer Algebra System[33] in our computations.
Example 1 Consider 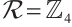 . Let
. Let 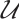 be a linear (submodule) code of length 11 over
be a linear (submodule) code of length 11 over 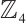 with a generator matrix
with a generator matrix 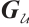 in standard form as follows:
in standard form as follows:
Set 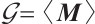 .i.e.,
.i.e., 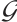 is a cyclic subgroup generated by
is a cyclic subgroup generated by 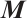 of
of 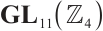 , where
, where
Clearly, 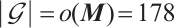 over
over 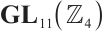 .
.
It is easy to see that 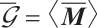 over
over 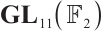 , where
, where
Thus, 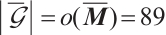 over
over 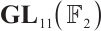 , and
, and 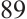 is a prime.
is a prime.
Take
By Lemma 8, 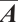 is a generator matrix of the linear code
is a generator matrix of the linear code 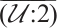 . By Theorem 3, we know
. By Theorem 3, we know
is a constant dimension code over 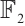 of dimension 4, length 11. One can check that
of dimension 4, length 11. One can check that 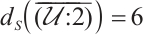 . This means that
. This means that 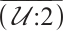 is a constant dimension code over
is a constant dimension code over 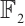 with parameters
with parameters 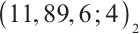 . Thus, by Theorem 3,
. Thus, by Theorem 3, 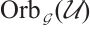 is an optimum distance constant dimension code over
is an optimum distance constant dimension code over 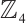 with parameters
with parameters 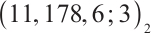 .
.
Remark 4 In Refs. [4, 6, 10-12, 34-35], the authors have proved the existence of constant dimension codes with size 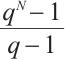 , or
, or 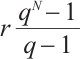 , or
, or 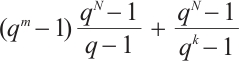 and minimal distance
and minimal distance 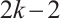 for any given
for any given 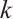 . Since
. Since 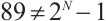 ,
, 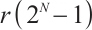 ,
, 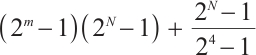 for any positive integers
for any positive integers 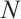 and
and 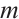 , the constant dimension code over
, the constant dimension code over 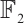 with parameters
with parameters 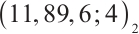 from Example 1 is new.
from Example 1 is new.
Example 2 Consider 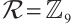 . Let
. Let 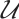 be a linear (submodule) code of length 7 over
be a linear (submodule) code of length 7 over 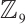 with a generator matrix
with a generator matrix 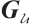 in standard form as follows:
in standard form as follows:
Set 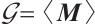 . i.e.,
. i.e., 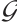 is a cyclic subgroup generated by
is a cyclic subgroup generated by 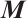 of
of 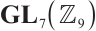 , where
, where
Clearly, 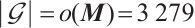 over
over 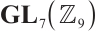 .
.
It is easy to check that 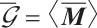 over
over 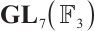 , where
, where
Thus, 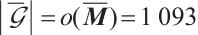 over
over 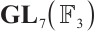 , and
, and 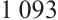 is a prime.
is a prime.
Take
By Lemma 8, 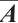 is a generator matrix of the linear code
is a generator matrix of the linear code 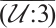 . Again by Theorem 3, we know
. Again by Theorem 3, we know  is a constant dimension code over
is a constant dimension code over 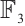 of dimension 3, length 6. One can check that
of dimension 3, length 6. One can check that 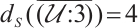 . This means that
. This means that 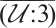 is a constant dimension code over
is a constant dimension code over 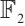 with parameters
with parameters 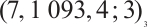 . Thus, by Theorem 3,
. Thus, by Theorem 3, 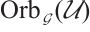 is a constant rank code over
is a constant rank code over 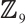 with parameters
with parameters 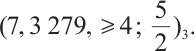
Remark 5 Glusing-Luerssen et al[4] gave an open problem: Cyclic orbit codes with maximum distance, that is, 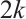 , are spread codes (A subspace code
, are spread codes (A subspace code 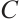 is called a spread of
is called a spread of 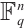 if
if 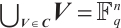 and
and 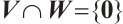 for all distinct
for all distinct 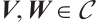 ). Thus, the best distance a non-spread cyclic orbit code of dimension k can attain is
). Thus, the best distance a non-spread cyclic orbit code of dimension k can attain is 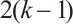 , but the construction of such codes is unknown. Examples 1 and 2 obtain two special such codes.
, but the construction of such codes is unknown. Examples 1 and 2 obtain two special such codes.
Remark 6 When the length and rank of a constant rank code 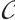 over
over 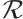 and a constant dimension code
and a constant dimension code 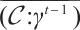 over
over 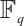 are same, we can see that
are same, we can see that 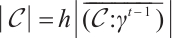 for some integer h>1 by Examples 1 and 2.
for some integer h>1 by Examples 1 and 2.
4 Gray Images of Constant Rank Code over 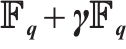
The ring 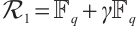 consists of all
consists of all 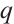 -ary polynomials of degree 0 and 1 in an indeterminate
-ary polynomials of degree 0 and 1 in an indeterminate 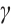 , and it is closed under
, and it is closed under 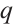 -ary polynomial addition and multiplication modulo
-ary polynomial addition and multiplication modulo 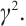 Thus
Thus 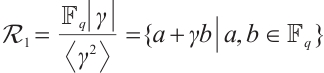 is a local ring with maximal ideal
is a local ring with maximal ideal 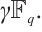 Therefore, it is a chain ring.
Therefore, it is a chain ring.
We first give the definition of the Gray map on 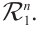 The Gray map
The Gray map 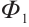 :
: 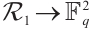 is given by
is given by 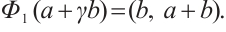 This map can be extended to
This map can be extended to 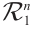 in a natural way:
in a natural way: 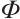 :
: 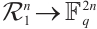 ,
, 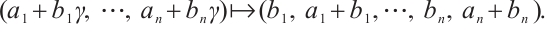 The following corollary and lemma are from Refs. [13, 16].
The following corollary and lemma are from Refs. [13, 16].
Corollary 3 ( Corollary 5.10 in Ref. [16]) If 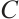 is a linear code over
is a linear code over 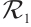 of length n and size
of length n and size 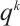 , then
, then 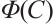 is a linear code over
is a linear code over 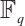 with parameters [2n, k].
with parameters [2n, k].
Lemma 11 ( Theorem 3.4 in Ref. [13]) Let 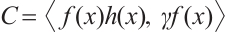 be a cyclic code of length n over
be a cyclic code of length n over 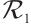 , where
, where 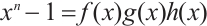 and
and 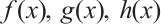 are pairwise coprime. Then
are pairwise coprime. Then 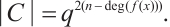
Lemma 12 Let 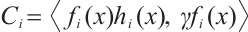 be a cyclic code of length n over
be a cyclic code of length n over 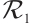 , where
, where 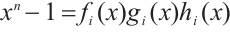 and
and 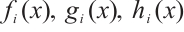 are pairwise coprime for
are pairwise coprime for 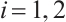 . Then
. Then 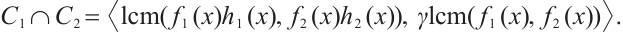 Moreover,
Moreover, 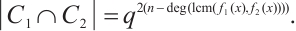
Proof Since  is a cyclic code of n over
is a cyclic code of n over 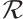 , there exist
, there exist 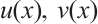 and
and 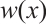 in
in 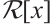 such that
such that 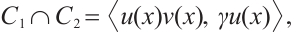 where
where 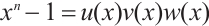 and
and 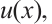
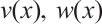 are pairwise coprime.
are pairwise coprime.
By 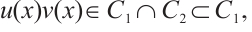 there exist
there exist 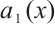 and
and 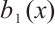 in
in 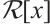 such that
such that 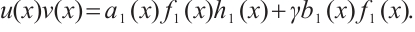 Multiplying by
Multiplying by 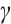 , we obtain
, we obtain 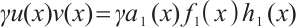 , which implies
, which implies 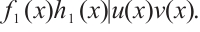
Again by 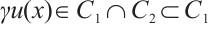 , there exist
, there exist 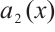 and
and 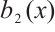 in
in 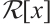 such that
such that 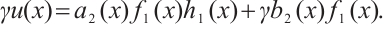 Multiplying by
Multiplying by 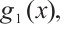 we obtain
we obtain 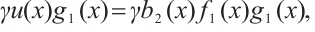 which implies
which implies 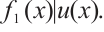
Similarly, 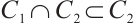 , which implies
, which implies 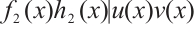 and
and 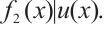
Consequently, 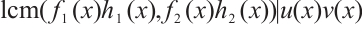 and
and 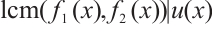 . This means that
. This means that
On the other hand, clearly, we have 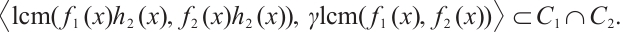
To summarize, we have 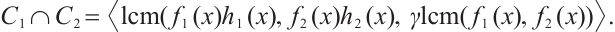
Set 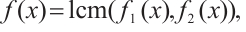
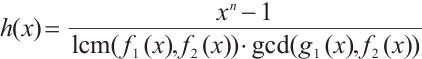 , and
, and 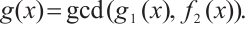
Then, 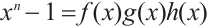 and the polynomials f(x), g(x) and h(x) are pairwise coprime.
and the polynomials f(x), g(x) and h(x) are pairwise coprime.
It is easy to check that 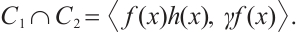 Therefore,
Therefore, 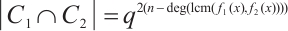 .
.
Now combining Corollary 3 with Lemmas 11 and 12, we obtain the following proposition.
Proposition 1 Let 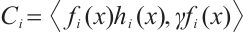 be a cyclic code of length n over
be a cyclic code of length n over 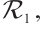 where
where 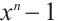

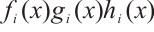 ,
, 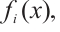
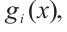
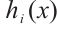 are pairwise coprime for
are pairwise coprime for 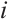

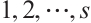 . Let
. Let 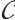
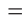
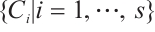 . If
. If 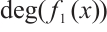

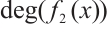

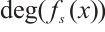 and
and 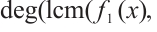
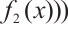

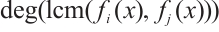 for all
for all 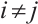 , then
, then 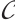 is a constant rank code over
is a constant rank code over 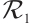 with parameters
with parameters 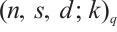 , where
, where 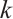

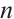

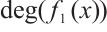 and d=
and d=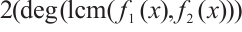
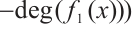 .
.
Corollary 4 Let 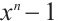

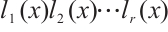 , where
, where 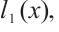
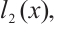
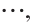
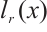 are pairwise coprime. We assume that
are pairwise coprime. We assume that 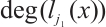



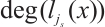 for
for 

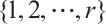 . Let
. Let 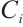

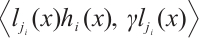 be a cyclic code of length n over
be a cyclic code of length n over 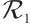 where
where 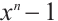

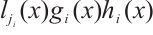 . Let
. Let 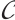
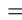
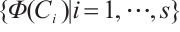 . Then
. Then 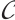 is an optimum constant dimension code
is an optimum constant dimension code 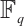 with parameters
with parameters 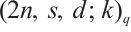 , where
, where 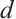

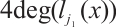 , and
, and 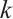

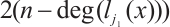 .
.
Proof It is easy to check that 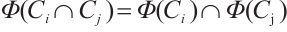 for
for 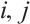

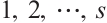 .
.
By Corollary 3 and Lemma 12, for 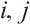

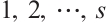 ,
, 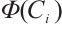 is a linear code over
is a linear code over 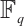 with parameters [2n, k], and
with parameters [2n, k], and 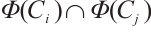 is a linear code over
is a linear code over 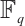 with parameters
with parameters 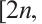
 . Thus,
. Thus, 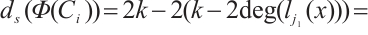
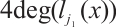 . So,
. So, 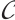 is an optimum constant dimension code
is an optimum constant dimension code 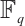 with parameters
with parameters 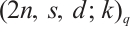 .
.
Example 3 Consider cyclic codes of length 71 over 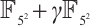 . In
. In 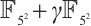 ,
,
where
Let 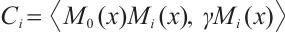 for
for 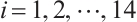 . Using Corollary 4, we find that the subspace code
. Using Corollary 4, we find that the subspace code 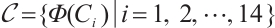 is an optimum distance constant dimension code over
is an optimum distance constant dimension code over 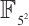 with parameters
with parameters 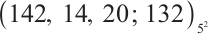 .
.
Example 4 Consider cyclic codes of lengths 84 and 93 over 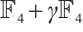 , respectively. First,
, respectively. First,
where
Let 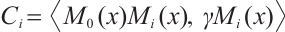 for
for 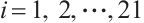 . Using Corollary 4, we find that the subspace code
. Using Corollary 4, we find that the subspace code 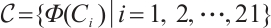 is an optimum distance constant dimension code over
is an optimum distance constant dimension code over 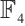 with parameters
with parameters 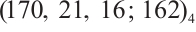 .
.
Second, taking n=93, we have
where
Let 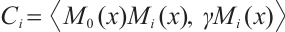 for
for 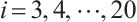 . Using Corollary 4, we find that the subspace code
. Using Corollary 4, we find that the subspace code 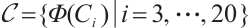 is an optimum distance constant dimension code over
is an optimum distance constant dimension code over 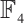 with parameters
with parameters 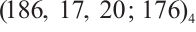 .
.
Remark 7 In Refs. [4, 6, 10-12, 34-35], the authors proved the existence of constant dimension codes with size 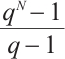 , or
, or 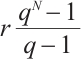 ,or
,or  and minimal distance
and minimal distance 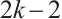 for any given
for any given 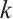 . Since 21,
. Since 21, 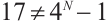 ,
, 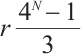 ,
,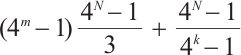 for any positive integers
for any positive integers 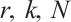 and
and 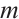 , the constant dimension codes over
, the constant dimension codes over 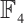 with parameters
with parameters 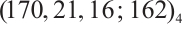 and
and 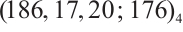 from Example 4 are new.
from Example 4 are new.
Remark 8 The constant dimension codes from Examples 3 and 4 are optimum distance constant dimension codes.
5 Conclusion
In this paper, we studied submodule codes over finite chain rings, and gave two criteria for a submodule code 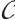 over finite chain rings to be a constant rank code. Further, we constructed optimum distance constant dimension codes over
over finite chain rings to be a constant rank code. Further, we constructed optimum distance constant dimension codes over 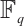 by using submodule codes in finite chain rings. We believe that submodule codes over finite chain rings will be a good source for constructing new constant dimension codes over
by using submodule codes in finite chain rings. We believe that submodule codes over finite chain rings will be a good source for constructing new constant dimension codes over 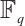 . In future work, in order to construct new constant dimension codes, we will use the computer algebra system MAGMA to search for more good submodule codes over finite chain rings.
. In future work, in order to construct new constant dimension codes, we will use the computer algebra system MAGMA to search for more good submodule codes over finite chain rings.
References
- Ahlswede R, Cai N, Li S R, et al. Network information flow[J]. IEEE Transactions on Information Theory, 2000, 46(4): 1204-1216. [Google Scholar]
- Koetter R, Kschischang F R. Coding for errors and erasures in random network coding[J]. IEEE Transactions on Information Theory, 2008, 54(8): 3579-3591. [Google Scholar]
- Gluesing-Luerssen H, Lehmann H. Distance distributions of cyclic orbit codes[J]. Designs, Codes and Cryptography, 2021, 89(3): 447-470. [Google Scholar]
- Gluesing-Luerssen H, Morrison K, Troha C. Cyclic orbit codes and stabilizer subfields[J]. Advances in Mathematics of Communications, 2015, 9(2): 177-197. [Google Scholar]
- Gluesing-Luerssen H, Troha C. Construction of subspace codes through linkage[J]. Advances in Mathematics of Communications, 2016, 10(3): 525-540. [Google Scholar]
- Chen B C, Liu H W. Constructions of cyclic constant dimension codes[J]. Designs, Codes and Cryptography, 2018, 86(6): 1267-1279. [Google Scholar]
- Heinlein D, Kurz S. Coset construction for subspace codes[J]. IEEE Transactions on Information Theory, 2017, 63(12): 7651-7660. [Google Scholar]
- Honold T, Kiermaier M, Kurz S. Optimal binary subspace codes of length 6, constant dimension 3 and minimum distance 4[EB/OL]. [2024-09-10]. https://arxiv.org/abs/1311.0464v2. [Google Scholar]
- Trautmann A L, Manganiello F, Braun M, et al. Cyclic orbit codes[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7386-7404. [Google Scholar]
- Ben-Sasson E, Etzion T, Gabizon A, et al. Subspace polynomials and cyclic subspace codes[J]. IEEE Transactions on Information Theory, 2016, 62(3): 1157-1165. [Google Scholar]
- Roth R M, Raviv N, Tamo I. Construction of Sidon spaces with applications to coding[J]. IEEE Transactions on Information Theory, 2018, 64(6): 4412-4422. [Google Scholar]
- Zhang H, Cao X W. Further constructions of cyclic subspace codes[J]. Cryptography and Communications, 2021, 13(2): 245-262. [Google Scholar]
- Dinh H Q, Lopez-Permouth S R. Cyclic and negacyclic codes over finite chain rings[J]. IEEE Transactions on Information Theory, 2004, 50(8): 1728-1744. [Google Scholar]
- Liu X S, Liu H L. LCD codes over finite chain rings[J]. Finite Fields and Their Applications, 2015, 34: 1-19. [Google Scholar]
- Hu P, Liu X S. Constacyclic codes of length ps over finite rings FPm+uFPm+vFPm+uvFPm[J]. Wuhan University Journal of Natural Sciences, 2020, 25(4): 311-322. [Google Scholar]
- Liu X S, Liu H L. σ-LCD codes over finite chain rings[J]. Designs, Codes and Cryptography, 2020, 88(4): 727-746. [Google Scholar]
- Liu X S, Liu H L. Quantum codes from linear codes over finite chain rings[J]. Quantum Information Processing, 2017, 16(10): 240. [Google Scholar]
- Liu Z H, Wang J L. Linear complementary dual codes over rings[J]. Designs, Codes and Cryptography, 2019, 87(12): 3077-3086. [Google Scholar]
- Norton G H, Sălăgean A. On the structure of linear and cyclic codes over a finite chain ring[J]. Applicable Algebra in Engineering, Communication and Computing, 2000, 10(6): 489-506. [Google Scholar]
- Abualrub T, Aydin N, Aydogdu I. Optimal binary codes derived from F2F4-additivecyclic codes[J]. Journal of Applied Mathematics and Computing, 2020, 64(1): 71-87. [Google Scholar]
- Bonnecaze A, Udaya P. Cyclic codes and self-dual codes over F2+uF2[J]. IEEE Transactions on Information Theory, 1999, 45(4): 1250-1255. [Google Scholar]
- Norton G H, Salagean A. On the Hamming distance of linear codes over a finite chain ring[J]. IEEE Transactions on Information Theory, 2000, 46(3): 1060-1067. [Google Scholar]
- Dinh H Q, Bag T, Upadhyay A K, et al. Quantum codes from a class of constacyclic codes over finite commutative rings[J]. Journal of Algebra and Its Applications, 2020, 19(12): 2150003. [Google Scholar]
- Kal X S, Zhu S X. Quaternary construction of quantum codes from cyclic codes over F4+uF4[J]. International Journal of Quantum Information, 2011, 9(2): 689-700. [Google Scholar]
- Liu H L, Liu X S. New EAQEC codes from cyclic codes over Fq+uFq[J]. Quantum Information Processing, 2020, 19(3): 85. [Google Scholar]
- Ma F, Gao J, Fu F W. Constacyclic codes over the ring FP+vFq and their applications of constructing new non-binary quantum codes[J]. Quantum Information Processing, 2018, 5(2):130-141. [Google Scholar]
- Tang Y S, Zhu S X, Kai X S, et al. New quantum codes from dual-containing cyclic codes over finite rings[J]. Quantum Information Processing, 2016, 15(11): 4489-4500. [Google Scholar]
- Dougherty S T, Liu H W. Independence of vectors in codes over rings[J]. Designs, Codes and Cryptography, 2009, 51(1): 55-68. [Google Scholar]
- MacWilliams F J, Sloane N J A. The Theory of Error-correcting Codes[M]. Amsterdam: Elsevier, 1977. [Google Scholar]
- Wood J A. Duality for modules over finite rings and applications to coding theory[J]. American Journal of Mathematics, 1999, 121(3): 555-575. [Google Scholar]
- Liu Z H. Galois LCD codes over rings[J]. Advances in Mathematics of Communications, 2024, 18(1): 91-104. [Google Scholar]
- Fan Y, Ling S, Liu H W. Matrix product codes over finite commutative Frobenius rings[J]. Designs, Codes and Cryptography, 2014, 71(2): 201-227. [Google Scholar]
- Bosma W, Cannon J, Playoust C. The magma algebra system I: The user language[J]. Journal of Symbolic Computation, 1997, 24(3/4): 235-265. [Google Scholar]
- Otal K, Özbudak F. Cyclic subspace codes via subspace polynomials[J]. Designs, Codes and Cryptography, 2017, 85(2): 191-204. [Google Scholar]
- Zhao W, Tang X L. A characterization of cyclic subspace codes via subspace polynomials[J]. Finite Fields and Their Applications, 2019, 57: 1-12. [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.