| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
|
|
|---|---|---|
| Page(s) | 289 - 301 | |
| DOI | https://doi.org/10.1051/wujns/2025303289 | |
| Published online | 16 July 2025 | |
Mathematics
CLC number: O236.2
Construction of Constant Rank and Orbit Codes over Finite Chain Rings
有限链环上常秩和轨道码的构造
Department of Science and Technology, College of Arts and Science of Hubei Normal University, Huangshi 435109, Hubei, China
† Corresponding author. E-mail: lxs6682@163.com
Received:
3
November
2024
In this paper, we first generalize the constant dimension and orbit codes over finite fields to the constant rank and orbit codes over finite chain rings. Then we provide a relationship between constant rank codes over finite chain rings and constant dimension codes over the residue fields. In particular, we prove that an orbit submodule code over a finite chain ring is a constant rank code. Finally, for special finite chain ring 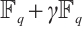 , we define a Gray map
, we define a Gray map 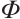 from
from 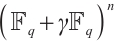 to
to 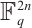 , and by using cyclic codes over
, and by using cyclic codes over 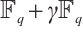 , we obtain a method of constructing an optimum distance constant dimension code over
, we obtain a method of constructing an optimum distance constant dimension code over 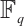 .
.
摘要
本文将有限域上常维数和轨道码推广到有限链环上的常秩和轨道码。我们提供了有限链环的常秩码和它的剩余类域的常维数码之间的一种关系。特别地,证明了有限链环上的轨道子模码是一个常秩码。最后,对于特殊有限链环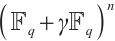 ,定义了一个Gray映射从
,定义了一个Gray映射从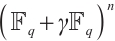 到
到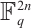 的Gray映射
的Gray映射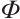 ,借助
,借助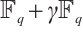 上的循环码,得到域
上的循环码,得到域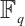 上一种构造极优距离常维数码的办法。
上一种构造极优距离常维数码的办法。
Key words: finite chain ring / rank of linear codes / constant rank codes / orbit codes
关键字 : 有限链环 / 线性码的秩 / 常秩码 / 轨道码
Cite this article: GUO Ye, LIU Xiusheng. Construction of Constant Rank and Orbit Codes over Finite Chain Rings[J]. Wuhan Univ J of Nat Sci, 2025, 30(3): 289-301.
Biography: GUO Ye, male, Master, Lecturer, research direction: algebraic coding. E-mail: 771088974@qq.com
Foundation item: Supported by Research Funds of Hubei Province (D20144401, Q20174503)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


