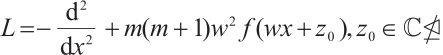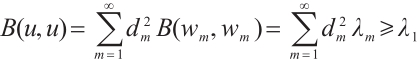| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 29, Number 3, June 2024
|
|
|---|---|---|
| Page(s) | 257 - 262 | |
| DOI | https://doi.org/10.1051/wujns/2024293257 | |
| Published online | 03 July 2024 | |
Mathematics
CLC number: O231.4
The Eigenvalue Properties of a Kind of Singular Differential Equations in 3-Dimensional Space
School of Mathematics and Statistics, Central South University, Changsha 410000, Hunan, China
† Corresponding author. E-mail: ghadirshokor@gmail.com
Received:
10
June
2023
In this paper, we consider the eigenvalue problem of the singular differential equation  in a bounded open ball with Dirichlet boundary condition in 3-dimensional space, where,
in a bounded open ball with Dirichlet boundary condition in 3-dimensional space, where, 
 ,
,  is a given constant
is a given constant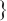 . And we have made a detailed characterization of the weak solution space. Furthermore, the existence of the minimum eigenvalue and the fundamental gap are provided.
. And we have made a detailed characterization of the weak solution space. Furthermore, the existence of the minimum eigenvalue and the fundamental gap are provided.
Key words: singular differential equation / eigenvalue / fundamental gap
Cite this article: GU Mengze, GHADIR Shokor. The Eigenvalue Properties of a Kind of Singular Differential Equations in 3-Dimensional Space[J]. Wuhan Univ J of Nat Sci, 2024, 29(3): 257-262.
Biography: GU Mengze, male, Ph. D. candidate, research direction: eigenvalue problem of differential operators. E-mail: 3059268737@gmail.com
© Wuhan University 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Consider the following equation:
where 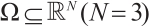 is an open and bounded ball with
is an open and bounded ball with  , 0
, 0 , and
, and  is a constant,
is a constant,  is the potential function, and
is the potential function, and  .
.
In the Sobolev space  , its norm is:
, its norm is:
or the equivalent norm:  (by using the Poincaré inequality).
(by using the Poincaré inequality).
Denote
In quantum mechanics, actually, the eigenvalue problem of operators in the theory of Hilbert space is mentioned by many researchers. In 2013, Tyagi[1] considered a singular eigenvalue problem involving Hardy's potential with Dirichlet boundary condition and gave that the problem possesses a continuous family of eigenvalues. Gesztesy and Zinchenko[2] showed the case of self-adjoint half-line Schrödinger operators on  with a potential strongly singular at the endpoint a. Nursultanov [3] found that asymptotic formulas for the eigenvalues of the Sturm-Liouville operator on the finite interval, with potentials having a strong negative singular at one endpoint. Haese-Hill [4] studied the spectral properties of its complex regularizations of the form:
with a potential strongly singular at the endpoint a. Nursultanov [3] found that asymptotic formulas for the eigenvalues of the Sturm-Liouville operator on the finite interval, with potentials having a strong negative singular at one endpoint. Haese-Hill [4] studied the spectral properties of its complex regularizations of the form:
where  is one of the half-periods of
is one of the half-periods of 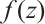 and
and 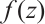 is the classical Weierstrass elliptic function. Li and Zhang [5] studied the numerical approximation of eigenvalue problems of the Schrödinger operator
is the classical Weierstrass elliptic function. Li and Zhang [5] studied the numerical approximation of eigenvalue problems of the Schrödinger operator  . Homa and Hryniv [6] proved analogues of the classical Sturm comparison and oscillation theorems for equations
. Homa and Hryniv [6] proved analogues of the classical Sturm comparison and oscillation theorems for equations  on a finite interval with real-valued distributional potentials.
on a finite interval with real-valued distributional potentials.
Due to the presence of singular terms such as  in the differential equation, the properties of the equation differ from those of traditional differential equations, constituting singular differential equations. The existence of this particular term makes it challenging to directly apply the classical Sobolev space framework and its related properties to the analysis of such equations. To effectively handle this singularity, this paper introduces weighted Sobolev spaces. Within this newly constructed framework, the existence, uniqueness, and regularity of solutions to singular differential equations are successfully established. The establishment of these properties not only deepens our understanding of solutions to singular differential equations but also lays a solid foundation for further research and applications.
in the differential equation, the properties of the equation differ from those of traditional differential equations, constituting singular differential equations. The existence of this particular term makes it challenging to directly apply the classical Sobolev space framework and its related properties to the analysis of such equations. To effectively handle this singularity, this paper introduces weighted Sobolev spaces. Within this newly constructed framework, the existence, uniqueness, and regularity of solutions to singular differential equations are successfully established. The establishment of these properties not only deepens our understanding of solutions to singular differential equations but also lays a solid foundation for further research and applications.
Additionally, a comprehensive description of spectral theory for singular differential equations is provided within this new framework. The characteristics of the equation's eigenvalues and eigenfunctions can be more accurately characterized by introducing weighted Sobolev spaces. This theory holds profound mathematical significance and offers new perspectives and methods for solving practical problems.
1 Preliminary
Lemma 1 The space  is a Hilbert space.
is a Hilbert space.
Proof Let  is a Cauchy sequence. Note that
is a Cauchy sequence. Note that  , then there exists
, then there exists  such that
such that  strongly in
strongly in  .
.
By using the Sobolev Embedding Theorem, we have  strongly in
strongly in  for
for  .
.
By using the Hardy-Sobolev inequality [7]:
 holds for
holds for  ,
,
where  is the completion of
is the completion of  in the norm:
in the norm:
We have:
which means that
So, we have  , and
, and
Then, there exists  such that
such that
 strongly in
strongly in 
and
which shows that  strongly in
strongly in  . From the assumptions
. From the assumptions  in
in  , then
, then  .
.
Denote
In the sense of distribution, for  ,
,  is a solution of the following equation
is a solution of the following equation
which is equivalent to the following equality:
Definition 1 (i) The bilinear form  associated with the elliptic operator
associated with the elliptic operator  defined by (2) is
defined by (2) is
(ii) We say that 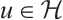 is a weak solution of the boundary-value problem (3) if
is a weak solution of the boundary-value problem (3) if
For all  , where
, where  denotes the inner product in
denotes the inner product in  .
.
Theorem 1 Let 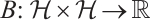 be defined as above. Then, there exist constants
be defined as above. Then, there exist constants  such that
such that
and
for all  .
.
Proof We readily check that:
for all  by Cauchy-Schwarz inequality.
by Cauchy-Schwarz inequality.
Then we have
by Lemma 1 and Poincaré inequality.
What's more, since  a.e., we can obtain that
a.e., we can obtain that
Corollary 1 Let 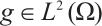 be a given function, then the elliptic equation
be a given function, then the elliptic equation  ,
, 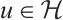 has a unique weak solution.
has a unique weak solution.
Proof By Theorem 1 and Lax-Milgram theorem, we can conclude the corollary.
Corollary 2 The operator  is a continuous, coercive, surjective, and linear operator, where
is a continuous, coercive, surjective, and linear operator, where  is the dual space of
is the dual space of  .
.
Proof It is evident that  is a linear operator.
is a linear operator.
Let  , by using the Lax-Milgram theorem[8], we can see that there exists a unique element
, by using the Lax-Milgram theorem[8], we can see that there exists a unique element  such that
such that
Note that  , thus
, thus
in the sense of distribution.
Consequently,  is a continuous, coercive, surjective, and linear operator.
is a continuous, coercive, surjective, and linear operator.
Lemma 2 Assume  , let u be a weak solution to the equation
, let u be a weak solution to the equation
Then  . Moreover,
. Moreover,
where  .
.
Proof (1) For all  , let
, let  be small such that
be small such that  . We take
. We take
Select a smooth function  satisfying
satisfying
Since  is a weak solution of (5), we have
is a weak solution of (5), we have  for all
for all  . Then
. Then
where  .
.
Set
Then, on the one hand, by the Cauchy equality with weight and difference quotient estimate, we have
On the other hand, by difference quotient estimate, we have
Thus, the Cauchy inequality with weight implies
where  is depend on
is depend on  .
.
Consequently,
From the difference quotient, we deduce  and thus
and thus  .
.
(2) For any  , according to (5)
, according to (5)
From which, Cauchy-Schwarz inequality and (1), we deduce that:
where we used Poincaré inequality in the equality, consequently, (6) holds.
Remark 1 Under the assumptions of the Lemma 2, (i) It seems that  since
since  is singular at
is singular at  ; (ii) From the Sobolev Embedding Theorem, it is clear that
; (ii) From the Sobolev Embedding Theorem, it is clear that  .
.
Proposition 1 Let  denotes the spectrum of L. Then
denotes the spectrum of L. Then  and
and  is at most countable. Let
is at most countable. Let  , where the eigenvalue is counted according to its multiplicity, then
, where the eigenvalue is counted according to its multiplicity, then
Finally, there exists an orthonormal basis  of
of  , where
, where  is an eigenfunction corresponding to
is an eigenfunction corresponding to  , that is
, that is
Proof Since  is a coercive, surjective, linear operator, set
is a coercive, surjective, linear operator, set 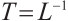 . From the Sobolev Compact Embedding theorem, we deduce that
. From the Sobolev Compact Embedding theorem, we deduce that 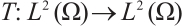 is a bounded, linear, compact operator. Hence
is a bounded, linear, compact operator. Hence  , the spectrum of
, the spectrum of 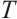 , is at most countable and has
, is at most countable and has  as the unique limit point.
as the unique limit point.
For any  , denote
, denote  ,
, 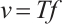 , then
, then
Thus,
which shows that  is a symmetric operator.
is a symmetric operator.
So, we say that  is a self-adjoint linear operator. And we thereby obtain the assertion of the Proposition by the Standard Functional Analysis 8 [8].
is a self-adjoint linear operator. And we thereby obtain the assertion of the Proposition by the Standard Functional Analysis 8 [8].
Lemma 3 Let  be the i-th eigenfunction with respect to the eigenfunction
be the i-th eigenfunction with respect to the eigenfunction  of
of  with the potential
with the potential  . Then,
. Then,
where,
Proof (i) Let  and
and  be defined as in Proposition 1. Then
be defined as in Proposition 1. Then
and
We observe that  is an orthonormal subset of
is an orthonormal subset of  under the new inner product
under the new inner product  . In fact, according to Theorem 1, Lemma 1, and the Poincaré inequality, we deduce that
. In fact, according to Theorem 1, Lemma 1, and the Poincaré inequality, we deduce that
i.e., these two norms  and
and  are equivalent on
are equivalent on  .
.
For arbitrary  with
with  ,
,  , it follows that
, it follows that  since
since  is an orthonormal basis of
is an orthonormal basis of  . Therefore
. Therefore
We obtain  ,
,  . Hence
. Hence  .
.
Finally, we have  is an orthonormal subset of
is an orthonormal subset of  under the new inner product
under the new inner product  .
.
(ii) Let  with
with  . Assume that
. Assume that  . We conclude that
. We conclude that
according to (i), this proves (7).
(iii) Suppose we have obtained  , for any
, for any  , with
, with  , then
, then  and
and  . Moreover,
. Moreover,
which implies that 
By (i), we have  , then the result (8) is obtained.
, then the result (8) is obtained.
2 Main Results
Theorem 2 There exists  ,
,  ,
,  , such that
, such that
and
where  is called the fundamental gap with potential
is called the fundamental gap with potential 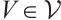 .
.
Proof we will show the proof by the following steps.
Step 1:  ,
,  exists.
exists.
For arbitrary  , we have
, we have  . Let
. Let  be such that
be such that
Then there exists a subsequence of  , still denoted by itself, and
, still denoted by itself, and  , such that
, such that  weakly star in
weakly star in  .
.
Denote  be the normalized first eigenfunction of
be the normalized first eigenfunction of  , which means that
, which means that  . From (4), we see
. From (4), we see
where  is the first eigenvalue of
is the first eigenvalue of  with the potential
with the potential  . Thus, there exists a subsequence of
. Thus, there exists a subsequence of  , still denoted by itself, and
, still denoted by itself, and 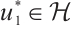 such that
such that
By  and Sobolev Embedding theorem, we deduce that
and Sobolev Embedding theorem, we deduce that
which implies that;
In view of Lemma 1, we have
then there exists a subsequence of  , still denoted by itself, and
, still denoted by itself, and  such that
such that
Hence,
which shows that  weakly in
weakly in  .
.
Thus (10) implies that
or we can say 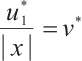 in
in  , i.e.
, i.e.
For all  ,
,
Since  and (12), we have
and (12), we have
Combining (9) (10) (11), we can obtain that
These imply that
Note that  , so in the sense of distribution, we have
, so in the sense of distribution, we have
This proves  is an eigenvalue of
is an eigenvalue of  with potential
with potential  . Therefore,
. Therefore,  by the definition of
by the definition of  .
.
Step 2: Choose  and
and  such that
such that
For each  , there exist
, there exist  ,
,  , such that
, such that  ,
,  are the first two normalized eigenfunctions with respect to the eigenvalues
are the first two normalized eigenfunctions with respect to the eigenvalues  and
and  with regard to
with regard to  . By the same argument as in Step 1, by abstracting subsequence, there exist
. By the same argument as in Step 1, by abstracting subsequence, there exist  ,
,  and
and  such that
such that
Moreover,
and
Consequently, on one side, owing to  , we obtain
, we obtain  . On the other side, by the same argument as Step 1, we deduce that:
. On the other side, by the same argument as Step 1, we deduce that:
This proves that  and
and  are eigenvalues of
are eigenvalues of  with potential
with potential  , in particular
, in particular  .
.
Obviously, the definition of  implies
implies  . Suppose
. Suppose  , then
, then  , i.e.,
, i.e.,  is the only eigenfunction of
is the only eigenfunction of  with potential according to Lemma 1. But the case
with potential according to Lemma 1. But the case  leads us to
leads us to  , a contradiction. This shows that
, a contradiction. This shows that  .
.
Step 3: Take arbitrary  , then
, then
Then there exists a subsequence of  , still denoted by itself, and
, still denoted by itself, and  such that
such that
Denote  ,
, 
 be the first and second normalized eigenfunctions with respect to
be the first and second normalized eigenfunctions with respect to  ,
,  , respectively. By the same argument as in Step 1, by abstracting subsequence, there exists
, respectively. By the same argument as in Step 1, by abstracting subsequence, there exists  ,
,  such that
such that
 and
and  weakly in
weakly in  .
.
By the same argument as in Step 2, we can deduce that
References
- Tyagi J. On an eigenvalue problem involving singular potential[J]. Complex Variables and Elliptic Equations, 2013,58(6): 865-871. [CrossRef] [MathSciNet] [Google Scholar]
- Gesztesy F, Zinchenko M. On spectral theory for Schrödinger operators with strongly singular potentials[J]. Mathematische Nachrichten, 2006, 279(9): 1041-1082. [CrossRef] [MathSciNet] [Google Scholar]
- Nursultanov M. Spectral Properties of Elliptic Operators in Singular Settings and Applications[D]. Gothenburg: University of Gothenburg, 2019. [Google Scholar]
- Haese-Hill W. Spectral Properties of Integrable Schrödinger Operators with Singular Potentials[D]. Loughborough: Loughborough University, 2015. [Google Scholar]
- Li H Y, Zhang Z M. Efficient spectral and spectral element methods for eigenvalue problems of Schrödinger equations with an inverse square potential[J]. SIAM Journal on Scientific Computing, 2017, 39(1): A114-A140. [NASA ADS] [CrossRef] [Google Scholar]
- Homa M, Hryniv R. Comparison and oscillation theorems for singular Sturm-Liouville operators[J]. Opuscula Mathematica, 2014, 34(1): 97-113. [CrossRef] [MathSciNet] [Google Scholar]
- Adimurthi, Chaudhuri N, Ramaswamy M. An improved Hardy-Sobolev inequality and its application[J]. Proceedings of the American Mathematical Society, 2001,130(2): 489-505. [Google Scholar]
- Brezis H. Functional Analysis, Sobolev Spaces and Partial Differential Equations[M]. New York: Springer-Verlag, 2010. [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.