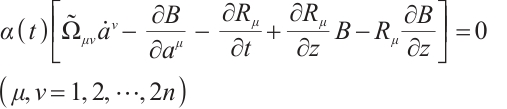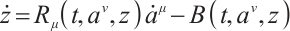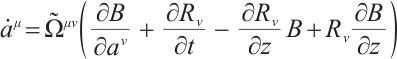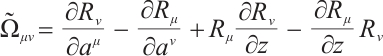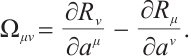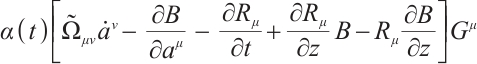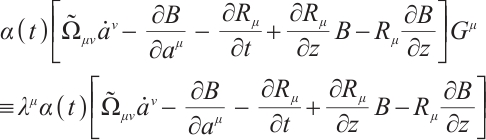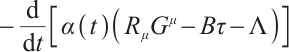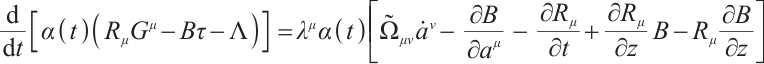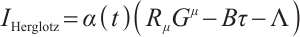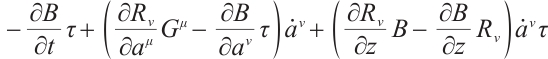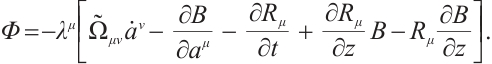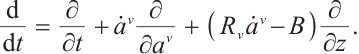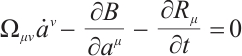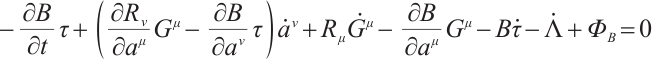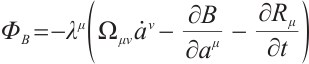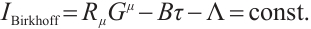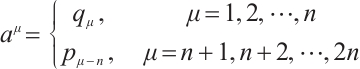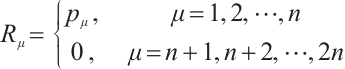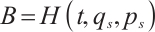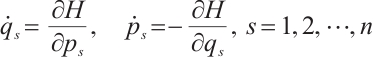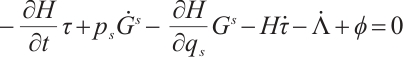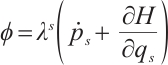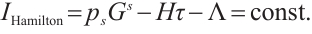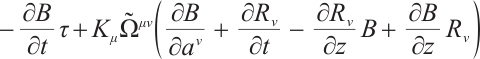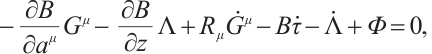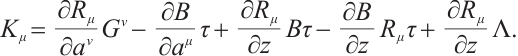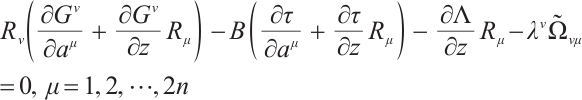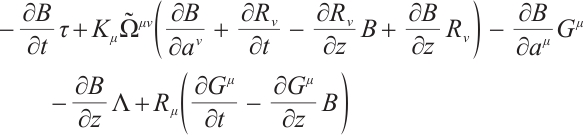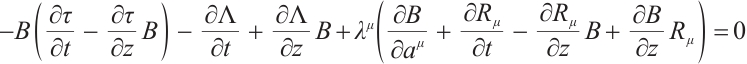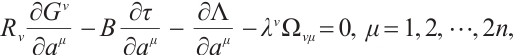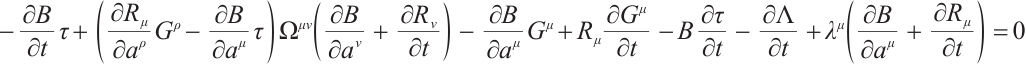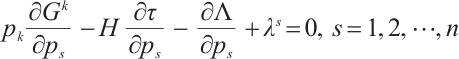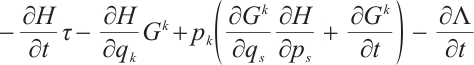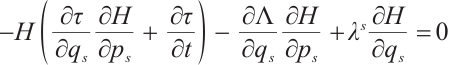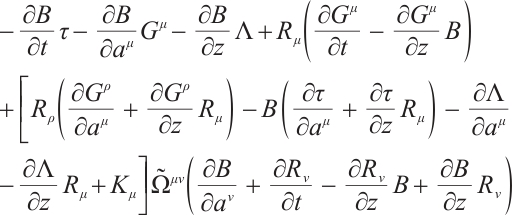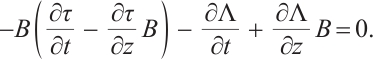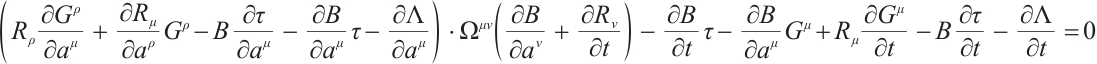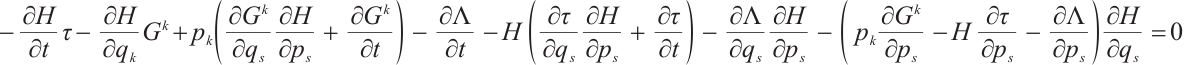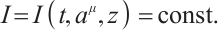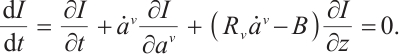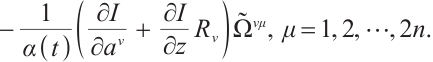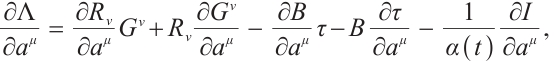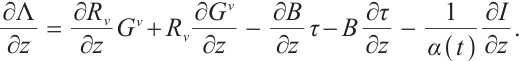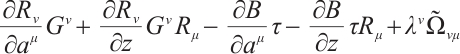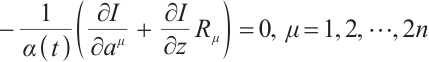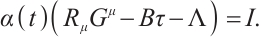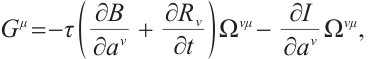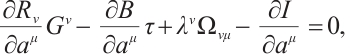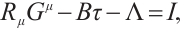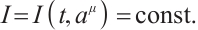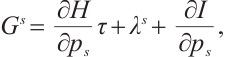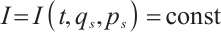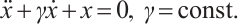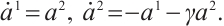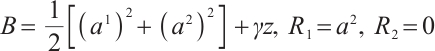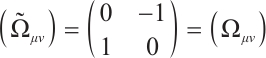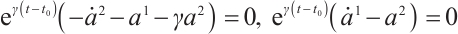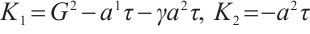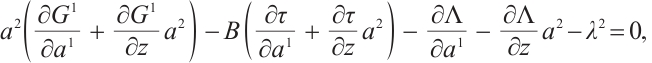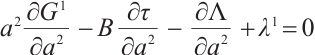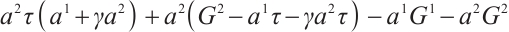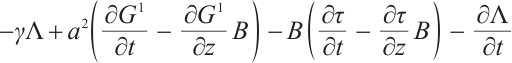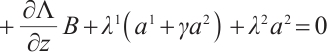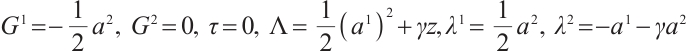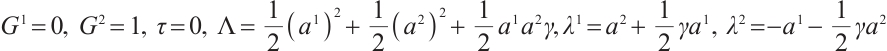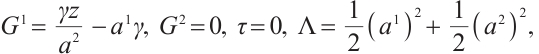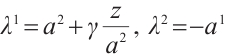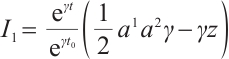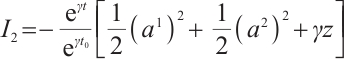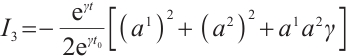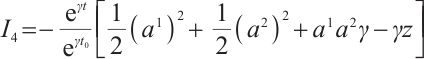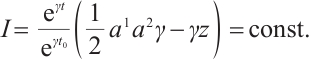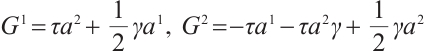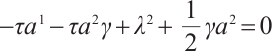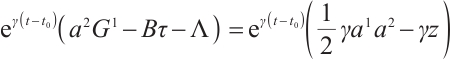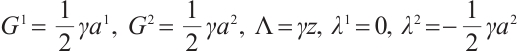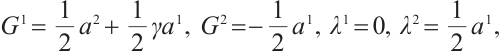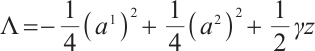| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 1, February 2025
|
|
|---|---|---|
| Page(s) | 49 - 56 | |
| DOI | https://doi.org/10.1051/wujns/2025301049 | |
| Published online | 12 March 2025 | |
Mathematics
CLC number: O316
Integrating Factors and Conservation Laws of Herglotz Type for Birkhoffian Systems
Herglotz型Birkhoff系统的积分因子与守恒律
1 School of Mathematical Sciences, Suzhou University of Science and Technology, Suzhou 215009, Jiangsu, China
2 College of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215011, Jiangsu, China
† Corresponding author. E-mail: zhy@mail.usts.edu.cn
Received:
1
June
2024
The method of integrating factors is used to study the conservation laws of the Herglotz type Birkhoffian systems in this paper. Firstly, the definition of the integrating factors of the Herglotz type Birkhoffian systems is given. Secondly, the relationship between the integrating factors and conservation laws is studied, and the conservation theorems of Herglotz type Birkhoff's equations and their inverse theorems are established. Thirdly, two types of generalized Killing equations for calculating integrating factors are given. Finally, as an example, a linear damped oscillator is taken. This example can be transformed into a Herglotz type Birkhoffian system. The resulting conservation theorems are used to find the conserved quantities for this example.
摘要
采用积分因子方法研究Herglotz型Birkhoff系统的守恒律。首先,给出了Herglotz型Birkhoff系统的积分因子的定义。 其次,研究了积分因子与守恒律之间的关系,建立了Herglotz型Birkhoff方程的守恒定理及其逆定理。第三,给出了计算积分因子的两类广义Killing方程。最后以线性阻尼振子为例,将其化为Herglotz型Birkhoff系统,利用所得到的守恒定理找到了该例的守恒律。
Key words: Birkhoffian system / Herglotz's variational principle / integrating factors / conservation law
关键字 : Birkhoff系统 / Herglotz变分原理 / 积分因子 / 守恒律
Cite this article: WANG Wenjing, ZHANG Yi. Integrating Factors and Conservation Laws of Herglotz Type for Birkhoffian Systems[J]. Wuhan Univ J of Nat Sci, 2025, 30(1): 49-56.
Biography: WANG Wenjing, female, Master candidate, research direction: analytical mechanics. E-mail: wenjing15617242792@163.com
Foundation item: Supported by the National Natural Science Foundation of China (12272248)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Conservation laws play a key role in exploring the dynamics of constrained mechanical systems. There are also plenty of ways to find conserved quantities, such as analytical mechanics methods[1], symmetry methods[2], and symmetry methods which includes Lie symmetry[3], Noether symmetry[4] and so on. Djukić et al[5] proposed to directly construct the conservation laws of nonconservative systems by multiplying the differential equations of motion by the integrating factors. Conserved quantities are calculated easily in this way. The integrating factors method has achieved a series of results in solving conserved quantities. Qiao et al[6,7] applied the integrating factors method to solve the conserved quantities in holonomic nonconservative systems. Since then, the integrating factors method has been generalized and applied to nonholonomic systems[8-10] and constrained Hamiltonian systems[11]. Birkhoffian mechanics[12,13] is a more general mechanics into which both holonomic and nonholonomic mechanics can be incorporated. Zhang[14,15] proposed to construct conservation laws of the Birkhoffian system by using the integrating factors method. The results are further generalized to constrained Birkhoffian systems[16] and fractional Birkhoffian systems[17].
Hamilton's principle, which is generally applicable to conservative systems, has encountered difficulties in generalizing to nonconservative systems. Existing nonconservative generalizations of Hamilton's principle are no longer variational principles, although differential equations of motion can be derived from them. Herglotz's principle[18], which defines its function through a differential equation, provides a variational principle for understanding systems that are by no means conservative. In 2002, Georgieva and Guenther[19] investigated the invariance of the Lagrangian function, a statement of Noether symmetry, and proved the Noether theorem of Herglotz type. Noether conservation laws of the Herglotz type were given, which marks the beginning of the research on the Noether symmetry of the Herglotz type. Recently, Herglotz type Noether theorems have been extended to nonconservative Lagrange systems[20-22], nonconservative Hamilton systems[23,24], nonholonomic systems[25-27], Birkhoffian systems[28,29], time-delay dynamics[30-33], fractional order dynamics [34-38], time-scale dynamics[39,40], etc.
Combining the integrating factors method with Birkhoffian systems and the Herglotz principle, this paper studies how to construct the conservation laws of the Herglotz type Birkhoffian system by using the integrating factors method. In Section 1, we define the integral factors of Herglotz Birkhoff's equation. Section 2 proposes the conservation theorems. The generalized Killing equations are derived in Section 3. The inverse theorems are established in Section 4. Herglotz type Birkhoff's equations are a generalization of classical Birkhoff's equations, and the latter is the generalization of Hamilton's equations. Therefore, we apply the obtained results to classical Birkhoff's equations and Hamilton's equations and discuss the corresponding theorems. In Section 5, the damped harmonic oscillator is taken as an example to demonstrate the application of the results. The last section is the conclusion of the article.
1 Herglotz Type Birkhoff's Equations and Its Integrating Factors
The Herglotz type Birkhoff's equations[28] are
where 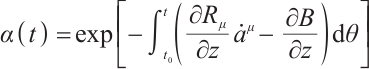 , and
, and  is the Pfaff-Herglotz action which is defined by
is the Pfaff-Herglotz action which is defined by
and 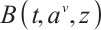 and
and 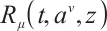 are the Birkhoffian and Birkhoff's functions in the sense of Herglotz, respectively. And
are the Birkhoffian and Birkhoff's functions in the sense of Herglotz, respectively. And 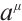 are Birkhoff's variables. Eq. (1) can be reduced to
are Birkhoff's variables. Eq. (1) can be reduced to
where 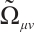 are called Herglotz type Birkhoff's tensor, there is
are called Herglotz type Birkhoff's tensor, there is
and 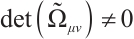 ,
,  .
.
If 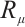 does not explicitly contain
does not explicitly contain 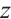 , then
, then 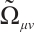 is reduced to Birkhoff's tensor
is reduced to Birkhoff's tensor 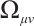 , i. e,
, i. e,
Definition 1 If there is a set of functions 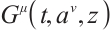 , such that this invariant
, such that this invariant
is reduced identically to
where 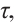
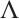 and
and 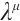 are functions of Birkhoff's variables
are functions of Birkhoff's variables 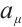 , time
, time 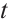 and functional
and functional 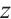 , then
, then 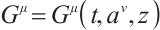 are named the integrating factors of Herglotz type Birkhoff's equations (1).
are named the integrating factors of Herglotz type Birkhoff's equations (1).
2 Conservation Theorems
Using Eqs. (1), we rewrite the formula (7) as
So, we can easily arrive at the theorem below:
Theorem 1 If 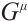 are integrating factors of Herglotz type Birkhoff's equations (1), then
are integrating factors of Herglotz type Birkhoff's equations (1), then
is the first integral along the trajectory of the Herglotz type Birkhoffian system.
For the Herglotz type Birkhoffian system (1), by Definition 1, if 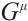 are its integrating factors, the necessary condition (7) should be satisfied. Expanding (7), we get
are its integrating factors, the necessary condition (7) should be satisfied. Expanding (7), we get
where
Hence, we have
Theorem 2 For the Herglotz type Birkhoffian system (1), if there exists a non-singular set of functions 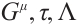 and
and 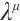 satisfying condition (10), then the system has a first integral such as (9).
satisfying condition (10), then the system has a first integral such as (9).
Remark 1 In deriving formula (10), we have adopted the operator to calculate 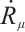 and
and 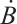 , namely:
, namely:
Remark 2 The functions 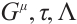 and
and 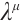 are called a singular set if they make the right side of the equation (9) a constant.
are called a singular set if they make the right side of the equation (9) a constant.
If there is no action z in the Birkhoffian functions 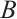 and
and 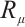 , Eq. (1) degenerate into the classical Birkhoff's equations
, Eq. (1) degenerate into the classical Birkhoff's equations
and Theorem 2 reduces to
Theorem 3 For the Birkhoffian system (13), if there exists a non-singular set of functions 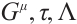 and
and 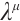 satisfying condition below:
satisfying condition below:
where
then the system has a first integral such as
Further, if[13]
then Eqs. (13) degenerate into the classical Hamilton's equations
and Theorem 3 reduces to
Theorem 4 For the Hamiltonian system (18), if there exists a non-singular set of functions 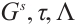 and
and 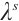 satisfying condition below:
satisfying condition below:
where
then the system has a first integral such as
Remark 3 The non-singular set of functions 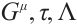 and
and 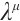 can be obtained by solving the necessary condition (10) (or (14), or (19)), and once a set of solutions is found, we can use Theorem 2 (or Theorem 3, or Theorem 4) to obtain a first integral of Herglotz type Birkhoffian systems (or classical Birkhoffian systems, or Hamiltonian systems).
can be obtained by solving the necessary condition (10) (or (14), or (19)), and once a set of solutions is found, we can use Theorem 2 (or Theorem 3, or Theorem 4) to obtain a first integral of Herglotz type Birkhoffian systems (or classical Birkhoffian systems, or Hamiltonian systems).
3 Generalized Killing Equations
The key to finding first integrals through Theorems 1 and 2 is to find non-singular sets of functions 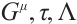 and
and 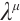 by solving equation (10).
by solving equation (10).
By substituting Eq. (3) into Eq. (10), we get
where
We expand Eq. (22) and decompose it into first-order partial differential equations for 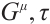 and
and 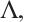 which are called generalized Killing equations. Solving the generalized Killing equations, it is possible to find these functions. In practice, we have the following two ways.
which are called generalized Killing equations. Solving the generalized Killing equations, it is possible to find these functions. In practice, we have the following two ways.
In the first way, we consider equation (22) to be true for arbitrary 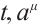 and
and 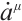 . Expand the Eq. (22) and let the coefficients of the terms
. Expand the Eq. (22) and let the coefficients of the terms 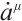 and the terms without
and the terms without 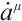 equal to zero respectively, we have
equal to zero respectively, we have
and
Eqs. (24) and (25) are named generalized Killing equations of Herglotz type Birkhoffian systems. So, we have
Theorem 5 For the Herglotz type Birkhoffian system (1), if there exists a non-singular set of functions 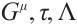 and
and 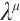 satisfying generalized Killing equations (24) and (25), then the system has a first integral such as (9).
satisfying generalized Killing equations (24) and (25), then the system has a first integral such as (9).
If 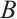 and
and 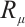 do not contain
do not contain 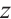 , Eqs. (24) and (25) degenerate into
, Eqs. (24) and (25) degenerate into
and
then Theorem 5 reduces to
Theorem 6 For the Birkhoffian system (13), if there exists a non-singular set of functions 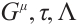 and
and 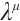 satisfying generalized Killing equations (26) and (27), then the system has a first integral such as (16).
satisfying generalized Killing equations (26) and (27), then the system has a first integral such as (16).
For classical Hamiltonian system (18), Eqs. (26) and (27) degenerate into
and
then Theorem 6 reduces to
Theorem 7 For the Hamiltonian system (20), if there exists a non-singular set of functions 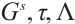 and
and  satisfying generalized Killing equations (28) and (29), then the system has a first integral such as (21).
satisfying generalized Killing equations (28) and (29), then the system has a first integral such as (21).
In the second way, we consider that Eq. (10) is true along the trajectory of Birkhoffian system (1), which means that  in Eq. (10) is not arbitrary, but is a function of
in Eq. (10) is not arbitrary, but is a function of 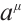 and
and 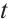 . Using Eqs. (3) and (11), Eq. (10) becomes
. Using Eqs. (3) and (11), Eq. (10) becomes
Eq. (30) is named generalized Killing equation of Herglotz type Birkhoffian systems along the dynamical trajectory. Then, we have
Theorem 8 For the Herglotz type Birkhoffian system (1), if there exists a non-singular set of functions 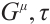 and
and 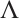 satisfying generalized Killing Eq. (30), then the system has a first integral such as (9).
satisfying generalized Killing Eq. (30), then the system has a first integral such as (9).
If 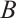 and
and 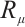 do not contain
do not contain 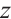 , Eq. (28) degenerates into
, Eq. (28) degenerates into
and Theorem 8 reduces to
Theorem 9 For the Birkhoffian system (13), if there exists a non-singular set of functions  and
and 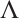 satisfying generalized Killing equations (31), then the system has a first integral such as (16).
satisfying generalized Killing equations (31), then the system has a first integral such as (16).
For classical Hamiltonian system (18), Eq. (31) degenerates into
and Theorem 9 reduces to
Theorem 10 For the Hamiltonian system (18), if there exists a non-singular set of functions 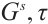 and
and 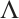 satisfying generalized Killing equation (32), then the system has a first integral such as (21).
satisfying generalized Killing equation (32), then the system has a first integral such as (21).
4 Inverse Theorems
Assume that the Herglotz type Birkhoffian system (1) has a first integral
By differentiating the Eq. (33), we get
Multiply Eq. (1) by 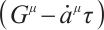 , then add it to Eq. (34), and let the coefficient of
, then add it to Eq. (34), and let the coefficient of 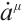 in the resulting equation equal to zero, we get
in the resulting equation equal to zero, we get
Taking the partial derivative of Eq. (9), we get
and
Substituting Eqs. (36) and (37) into (24), we get
Let Eq. (33) equal the first integral (9), we have
Hence, we have the theorem below.
Theorem 11 If Herglotz type Birkhoffian system (1) has a first integral (33), then its integrating factors, 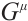 and functions
and functions 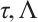 and
and 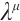 are determined by Eqs. (35), (38) and (39).
are determined by Eqs. (35), (38) and (39).
Remark 4 Formulas (35), (38) and (39) are 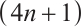 equations with
equations with 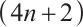 variables
variables 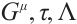 and
and 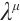 , and obviously their solutions are not unique. In practical application, we can choose one variable appropriately to obtain the integrating factors
, and obviously their solutions are not unique. In practical application, we can choose one variable appropriately to obtain the integrating factors 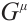 .
.
If 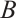 and
and 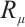 do not contain
do not contain 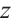 , Eqs. (35), (38) and (39) degenerate into
, Eqs. (35), (38) and (39) degenerate into
and Theorem 11 reduces to
Theorem 12 If the Birkhoffian system (13) has a first integral
then its integrating factors 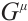 and functions
and functions 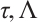 and
and 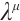 are determined by Eqs. (40), (41) and (42).
are determined by Eqs. (40), (41) and (42).
For classical Hamiltonian system (18), Eqs. (40)-(42) degenerate into
and Theorem 12 reduces to
Theorem 13 If the Hamiltonian system (18) has a first integral
then its integrating factors  and functions
and functions  and
and 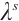 are determined by Eqs. (44) and (45).
are determined by Eqs. (44) and (45).
5 Example
Consider a nonconservative system
First, we establish Herglotz type Birkhoff's equations. Let 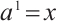 and
and 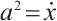 , then Eq. (47) is reduced to
, then Eq. (47) is reduced to
Eq. (48) can be expressed as a Herglotz type Birkhoffian system[28], where
Using Eqs. (4) and (5), we get
Substituting formulas (49) and (50) into Eq. (1), we get
This is Herglotz type Birkhoff's equations corresponding to Eqs. (1).
Second, we study the positive problem of finding conserved quantities. From (23), we have
The generalized Killing Eqs. (24) and (25) read
and
Eqs. (53)-(55) have the following solutions
According to Theorem 2, the system has first integrals as follows
Finally, we study the inverse problem. Suppose that the system has a first integral
By using equation (35), we get
and by equations (38) and (39), we get
Eqs. (65)-(68) have a total of five equations with six unknowns, so the solutions are not unique.
If we take 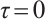 , then we obtain
, then we obtain
If we take 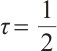 , then we obtain
, then we obtain
6 Conclusion
Conservation laws are crucial in the local description of physical states and kinetic behavior, the reduction of differential equations of motion, and the stability of motion, etc. The integral factors method proposed by Djukić to construct conservation laws is simple, convenient and effective. In this paper, we extended the method to Herglotz Birkhoffian system. The new points of this paper are as follows:
1) Integrating factors of Herglotz type Birkhoffian systems are defined, the necessary condition for the existence of conserved quantities are deduced, the conservation theorems (Theorem 1 and Theorem 2) and their special cases for classical Birkhoffian systems (Theorem 3) and Hamiltonian systems (Theorem 4) are given.
2) Generalized Killing equations are established, from which integrating factors determining conservation laws can be found. According to the necessary condition of conserved quantities and considering the dependence of variables, two ways of determining integrating factors are given, which are summarized as Theorem 5 to Theorem 10.
3) The inverse theorems of conservation theorems are given, that is, if a conserved quantity is known, how to determine its integrating factors. The results are summarized as Theorem 11 to Theorem 13.
References
- Mei F X. Advances in the symmetries and conserved quantities of classical constrained systems[J]. Advances in Mechanics, 2009, 39(1): 37-43(Ch). [Google Scholar]
- Mei F X. Analytical Mechanics Ⅱ[M]. Beijing: Beijing Institute of Technology Press, 2013(Ch). [Google Scholar]
- Chen J Y, Zhang Y. Lie symmetry theorem for nonshifted Birkhoffian systems on time scales[J]. Wuhan University Journal of Natural Sciences, 2022, 27(3): 211-217. [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang Y. A study on time scale non-shifted Hamiltonian dynamics and Noether's theorems[J]. Wuhan University Journal of Natural Sciences, 2023, 28(2): 106-116. [CrossRef] [EDP Sciences] [Google Scholar]
- Djukic D S, Sutela T. Integrating factors and conservation laws for nonconservative dynamical systems[J]. International Journal of Non Linear Mechanics, 1984, 19(4): 331-339. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Qiao Y F, Zhang Y L, Zhao S H. Integrating factors and conservation laws for the Raitzin's canonical equations of motion of nonconservative dynamical systems[J]. Acta Physica Sinica, 2002, 51(8): 1661-1665(Ch). [CrossRef] [MathSciNet] [Google Scholar]
- Qiao Y F, Zhang Y L, Han G C. Integrating factors and conservation theorem for holonomic nonconservative dynamical systems in generalized classical mechanics[J]. Chinese Physics, 2002, 11(10): 988-992. [Google Scholar]
- Qiao Y F, Zhao S H, Li R J. Integrating factors and conservation theorems of nonholonomic dynamical system of relative motion[J]. Communications in Theoretical Physics, 2007, 47(2): 217-220. [NASA ADS] [CrossRef] [Google Scholar]
- Zhang Y. A study of conservation laws for Chaplygin nonholonomic systems by means of integrating factors method[J]. Journal of Dynamics and Control, 2019, 17(1): 15-20(Ch). [Google Scholar]
- Zhang Y, Ge W K. Integrating factors and conservation laws for non-holonomic dynamical systems[J]. Acta Physica Sinica, 2003, 52(10): 2363-2367(Ch). [CrossRef] [MathSciNet] [Google Scholar]
- Zhou J R, Fu J L. The integrating factor and conservation quantity for constrained Hamilton system[J]. Chinese Quarterly of Mechanics, 2018, 39(3): 554-561(Ch). [Google Scholar]
- Santilli R M. Foundations of Theoretical Mechanics II[M]. Berlin, Heidelberg: Springer-Verlag, 1983. [CrossRef] [Google Scholar]
- Mei F X, Shi R C, Zhang Y F, et. al. Dynamics of Birkhoffian System[M]. Beijing: Beijing Institute of Technology Press, 1996(Ch). [Google Scholar]
- Zhang Y, Xue Y. Integrating factors and conservation theorems for Birkhoffian systems[J]. Chinese Quarterly of Mechanics, 2003, 24(2): 280-285(Ch). [Google Scholar]
- Yi Z. A general approach to the construction of conservation laws for Birkhoffian systems in event space[J]. Communications in Theoretical Physics, 2008, 50(4): 851-854. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Qiao Y F, Zhao S H, Li R J. Integrating factors and conservation theorems of constrained Birkhoffian systems[J]. Chinese Physics, 2006, 15(12): 2777-2781. [NASA ADS] [CrossRef] [Google Scholar]
- Yang L X, Zhang Y. Integrating factors and conserved quantities for fractional Birkhoffian system[J]. Journal of Central China Normal University (Natural Sciences), 2020, 54(1): 30-35(Ch). [MathSciNet] [Google Scholar]
- Guenther R B, Guenther C M, Gottsch J A. The Herglotz Lectures on Contact Transformations and Hamiltonian Systems[M]. Nicolaus: Copernicus University Press, 1996. [Google Scholar]
- Georgieva B, Guenther R B. First Noether-type theorem for the generalized variational principle of Herglotz[J]. Topological Methods in Nonlinear Analysis, 2002, 20(2): 261-273. [CrossRef] [MathSciNet] [Google Scholar]
- Tian X, Zhang Y. Generalized variational principle of Herglotz type for non-conservative Lagrangian systems and its Noether's theory[J]. Journal of Nanjing University of Science and Technology, 2019, 43(6): 765-770(Ch). [MathSciNet] [Google Scholar]
- Cai J X, Zhang Y. Nother's theorem for Herglotz-type nonconservative Lagrange systems in event space[J]. Chinese Quarterly of Mechanics, 2022, 43(1): 122-131(Ch). [Google Scholar]
- Cai M Y, Zhang Y. Herglotz type Lagrange equations and Noether symmetry and conserved quantity for mechanical systems with variable mass[J]. Journal of Dynamics and Control, 2022, 20(6): 107-113(Ch). [Google Scholar]
- Zhang Y. Generalized variational principle of Herglotz type for nonconservative system in phase space and Noether's theorem[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(6): 1382-1389(Ch). [Google Scholar]
- Zhang Y, Cai J X. Noether theorem of Herglotz-type for nonconservative Hamilton systems in event space [J]. Wuhan University Journal of Natural Sciences, 2021, 26(5): 376-382. [Google Scholar]
- Zhang Y, Tian X. Conservation laws of nonconservative nonholonomic system based on Herglotz variational problem[J]. Physics Letters A, 2019, 383(8): 691-696. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dong X C, Zhang Y. Herglotz-type principle and first integrals for nonholonomic systems in phase space[J]. Acta Mechanica, 2023, 234(12): 6083-6095. [CrossRef] [MathSciNet] [Google Scholar]
- Dong X C, Zhang Y. Herglotz type conservation laws for nonconservative nonholonomic systems[J]. AIP Advances, 2023, 13(10): 105014. [CrossRef] [Google Scholar]
- Zhang Y. Variational problem of Herglotz type for Birkhoffian system and its Noether's theorems[J]. Acta Mechanica, 2017, 228(4): 1481-1492. [CrossRef] [MathSciNet] [Google Scholar]
- Zhang Y, Tian X. Conservation laws for Birkhoffian systems of Herglotz type[J]. Chinese Physics B, 2018, 27(9): 090502. [NASA ADS] [CrossRef] [Google Scholar]
- Santos S P S, Martins N, Torres D F M. Variational problems of Herglotz type with time delay: DuBois: Reymond condition and Noether's first theorem[J]. Discrete & Continuous Dynamical Systems-A, 2015, 35(9): 4593-4610. [CrossRef] [MathSciNet] [Google Scholar]
- Santos S P S, Martins N, Torres D F M. Noether currents for higher-order variational problems of Herglotz type with time delay[J]. Discrete and Continuous Dynamical Systems-Series S, 2018, 11(1): 91-102. [CrossRef] [MathSciNet] [Google Scholar]
- Zhang Y. Noether's theorem for a time-delayed Birkhoffian system of Herglotz type[J]. International Journal of Non Linear Mechanics, 2018, 101: 36-43. [NASA ADS] [CrossRef] [Google Scholar]
- Zhang Y. Herglotz's variational problem for non-conservative system with delayed arguments under Lagrangian framework and its Noether's theorem[J]. Symmetry, 2020, 12(5): 845. [NASA ADS] [CrossRef] [Google Scholar]
- Almeida R, Malinowska A B. Fractional variational principle of Herglotz[J]. Discrete & Continuous Dynamical Systems-B, 2014, 19(8): 2367-2381. [CrossRef] [MathSciNet] [Google Scholar]
- Atanacković T M, Janev M, Pilipović S. Noether's theorem for variational problems of Herglotz type with real and complex order fractional derivatives[J]. Acta Mechanica, 2021, 232(3): 1131-1146. [CrossRef] [MathSciNet] [Google Scholar]
- Xu X X, Zhang Y. A new type of adiabatic invariant for fractional order non-conservative Lagrangian systems[J]. Acta Physica Sinica, 2020, 69(22): 220401. [CrossRef] [Google Scholar]
- Tian X, Zhang Y. Noether's theorem for fractional Herglotz variational principle in phase space[J]. Chaos, Solitons & Fractals, 2019, 119: 50-54. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ding J J, Zhang Y. Noether's theorem for fractional Birkhoffian system of Herglotz type with time delay[J]. Chaos, Solitons & Fractals, 2020, 138: 109913. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Tian X, Zhang Y. Variational principle of Herglotz type and its Noether's theorem on time scales[J]. Chinese Quarterly of Mechanics, 2018, 39(2): 237-248(Ch). [Google Scholar]
- Tian X, Zhang Y. Noether symmetry and conserved quantity for Hamiltonian system of Herglotz type on time scales[J]. Acta Mechanica, 2018, 229(9): 3601-3611. [CrossRef] [MathSciNet] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.