| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 1, February 2025
|
|
|---|---|---|
| Page(s) | 57 - 59 | |
| DOI | https://doi.org/10.1051/wujns/2025301057 | |
| Published online | 12 March 2025 | |
Mathematics
CLC number: O156
On the Coprime Labelings of Hypergraph
超图的互素标号问题研究
1 School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming 650221, Yunnan, China
2 School of Mathematics and Statistics, Yangtze Normal University, Chongqing 408102, China
† Corresponding author. E-mail: zhangshaohua@yznu.edu.cn
Received:
12
September
2024
Graph labeling is the assignment of integers to the vertices, edges, or both, subject to certain conditions. Accordingly, hypergraph labeling is also the assignment of integers to the vertices, edges, or both, subject to certain conditions. This paper is to generalize the coprime labelings of graph to hypergraph. We give the definition of coprime labelings of hypergraph. By using Rosser-Schoenfeld's inequality and the coprime mapping theorem of Pomerance and Selfridge, we prove that some linear hypergraphs are prime.
摘要
图标号是在一定条件下将整数分配给图的顶点或边,或两者兼有,使其满足一定条件。因此超图的标号也可以在一定条件下将整数分配到超图的顶点或边上,或两者兼有,使其满足一定条件。本文将图的互素标号问题推广到超图,进一步给出了超图互素标号的定义,利用Rosser-Schoenfeld不等式和Pomerance 和Selfridge的互素映射定理,证明了一些线性超图是素超图。
Key words: coprime mapping theorem of Pomerance and Selfridge / linear hypergraphs / prime hypergraphs
关键字 : Pomerance和Selfridge的互素映射定理 / 线性超图 / 素超图
Cite this article: ZHANG Zizhou, ZHANG Shaohua. On the Coprime Labelings of Hypergraph[J]. Wuhan Univ J of Nat Sci, 2025, 30(1): 57-59.
Biography: ZHANG Zizhou, male, Undergraduate, research direction: statistics. E-mail: 3200118@qq.com
Foundation item: Supported by the Natural Science Foundation of Chongqing (CSTB2022NSCQ-MSX0884)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Graph labeling is one of the most important research problems in graph theory, and the coprime labeling of graph is one of the hottest issues, which has attracted the attention of many mathematicians. Graph labeling is the assignment of integers to the vertices, edges, or both, subject to certain conditions. Graph labelings were first introduced in the middle of 1960s. In the intervening 60 years, over 200 graph labeling techniques have been studied in over 2 000 papers[1]. A graph  with vertices set
with vertices set  is said to have coprime labeling if its vertices are labeled with distinct integers
is said to have coprime labeling if its vertices are labeled with distinct integers  such that for each edge
such that for each edge  the labels assigned to
the labels assigned to  and
and  are relatively prime. If such a labeling exists, then
are relatively prime. If such a labeling exists, then  is said to be prime. Prime graphs have been of interest since the 1980s and were popularized by the Entringer-Tout Tree Conjecture which states that all trees are prime. In 1994, Fu and Huang[2] showed that all trees of order up to 15 are prime. In 2007, Pikhurko[3] proved that all trees of order up to 50 are prime. The classes of trees known to have prime labelings are paths, stars, caterpillars, complete binary trees, spiders, olive trees, palm trees, banana trees, binomial trees and so on[4]. In 2011, Haxell et al[5] proved that all large trees are prime. In this paper, we will try to generalize the coprime labelings of graph to hypergraph.
is said to be prime. Prime graphs have been of interest since the 1980s and were popularized by the Entringer-Tout Tree Conjecture which states that all trees are prime. In 1994, Fu and Huang[2] showed that all trees of order up to 15 are prime. In 2007, Pikhurko[3] proved that all trees of order up to 50 are prime. The classes of trees known to have prime labelings are paths, stars, caterpillars, complete binary trees, spiders, olive trees, palm trees, banana trees, binomial trees and so on[4]. In 2011, Haxell et al[5] proved that all large trees are prime. In this paper, we will try to generalize the coprime labelings of graph to hypergraph.
Hypergraphs, an extension of traditional graphs, have found wide applications in various fields. Hypergraph labeling, similar to graph labeling, is a crucial concept with significant implications. It provides a way to assign integers to vertices, edges, or both in a hypergraph, which is not only fundamental for understanding the structural properties of hypergraphs but also serves as a powerful tool in solving practical problems. By carefully defining and analyzing hypergraph labelings, mathematicians can gain insights into the internal structure of hypergraphs, and this understanding can be applied to optimize algorithms, design efficient communication networks, and analyze complex systems. Like the coprime labeling of graphs, we expect that the coprime labelings of hypergraphs will have more significant applications and theoretical value.
1 Motivation and Main Results
Note that a hypergraph is a graph in which generalized edges (called hyperedges) may connect more than two vertices. Formally, a hypergraph  is a pair
is a pair 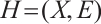 , where
, where  is a set of elements, called vertices, and
is a set of elements, called vertices, and  is a set of non-empty subsets of
is a set of non-empty subsets of  called hyperedges. Naturally, the coprime labelings of a graph can be generalized to the hypergraph. A hypergraph of order
called hyperedges. Naturally, the coprime labelings of a graph can be generalized to the hypergraph. A hypergraph of order  is prime if its vertices are labeled with distinct integers
is prime if its vertices are labeled with distinct integers  ,so that there is at least one number in a hyperedge, which is coprime to the rest numbers in that hyperedge. Namely, let
,so that there is at least one number in a hyperedge, which is coprime to the rest numbers in that hyperedge. Namely, let  be a hypergraph with
be a hypergraph with  hyperedg:
hyperedg:
and let  and
and  . If its all vertices
. If its all vertices  are labeled with distinct integers
are labeled with distinct integers  so that for
so that for , there is at least
, there is at least  in
in  satisfying
satisfying
 , then we call
, then we call  a prime hypergraph. Here we must point out that each hyperedge includes at least two vertices. We do not consider isolated points or single cycles because they must satisfy the condition of being coprime. Thus, the coprime labeling of hypergraphs is essentially a number theoretical problem. A hypergraph is linear if any two hyperedges have at most one common vertex. Clearly, a tree is a special linear hypergraph. The result by Haxell, Pikhurko and Taraz[5] shows that all large trees are prime hypergraphs. Here, we will prove that certain types of linear hypergraphs are prime. However, it remains unknown whether all linear hypergraphs are prime hypergraphs. We present the following theorems.
a prime hypergraph. Here we must point out that each hyperedge includes at least two vertices. We do not consider isolated points or single cycles because they must satisfy the condition of being coprime. Thus, the coprime labeling of hypergraphs is essentially a number theoretical problem. A hypergraph is linear if any two hyperedges have at most one common vertex. Clearly, a tree is a special linear hypergraph. The result by Haxell, Pikhurko and Taraz[5] shows that all large trees are prime hypergraphs. Here, we will prove that certain types of linear hypergraphs are prime. However, it remains unknown whether all linear hypergraphs are prime hypergraphs. We present the following theorems.
Theorem 1 If any two hyperedges of a linear hypergraph  have no common vertex, then
have no common vertex, then  is a prime hypergraph.
is a prime hypergraph.
Theorem 2 If a linear hypergraph  has
has  hyperedges and each hyperedge has
hyperedges and each hyperedge has  vertices, then when
vertices, then when  ,
,  is a prime hypergraph.
is a prime hypergraph.
2 Proofs of Main Results
Lemma 1 (Coprime mapping theorem by Pomerance and Selfridge[6]) If  is a positive integer and
is a positive integer and is a set of
is a set of  consecutive integers, then there is a bijection
consecutive integers, then there is a bijection :
: such that
such that  for
for  . We call such
. We call such  a coprime mapping.
a coprime mapping.
Proof of Theorem 1 Suppose that the linear hypergraph  has
has  hyperedges and the numbers of vertices in each hyperedge are
hyperedges and the numbers of vertices in each hyperedge are  , respectively. Without losing generality, we assume that
, respectively. Without losing generality, we assume that 
 . Suppose that vertices in the i-th hyperedge are labeled with distinct integers
. Suppose that vertices in the i-th hyperedge are labeled with distinct integers  . Note that any two hyperedges have no common vertex. Therefore, we obtain an echelon form:
. Note that any two hyperedges have no common vertex. Therefore, we obtain an echelon form:
Firstly, we identify the first column:  ,
, 
 . So,
. So,  are exactly the consecutive positive integers:
are exactly the consecutive positive integers:  . Secondly, we consider how to label the second column
. Secondly, we consider how to label the second column  . By Lemma 1, there is a coprime mapping between
. By Lemma 1, there is a coprime mapping between  and
and  . Let
. Let  be the permutation of
be the permutation of  such that
such that (
( ). Therefore, the echelon form becomes the following shape:
). Therefore, the echelon form becomes the following shape:
Thirdly, we consider how to label the third column  . If the third column still has
. If the third column still has  elements, then by Lemma 1, there is a coprime mapping between
elements, then by Lemma 1, there is a coprime mapping between  and
and  . If there are only
. If there are only  elements in the third column and
elements in the third column and  , then by Lemma 1, there is a coprime mapping between
, then by Lemma 1, there is a coprime mapping between  and
and 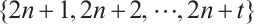 . Let
. Let  be the permutation of
be the permutation of  such that
such that  ,
,  . Therefore, the echelon form becomes the possible shape:
. Therefore, the echelon form becomes the possible shape:
Note that one is coprime to any natural number. Therefore, one can repeat this process and use the coprime mapping theorem repeatedly until all vertices are labeled such that  with
with  . Therefore,
. Therefore,  is a prime hypergraph and the proof is complete.
is a prime hypergraph and the proof is complete.
Lemma 2 (Rosser-Schoenfeld's inequality[7]) For ,
, , where
, where is the number of prime numbers which are less than or equal to
is the number of prime numbers which are less than or equal to  .
.
Proof of Theorem 2 If a linear hypergraph  has
has  hyperedges, and each hyperedge has
hyperedges, and each hyperedge has  vertices, then every hyperedge of
vertices, then every hyperedge of  has a vertex, which does not belong to any other hyperedges. Denote these vertices by
has a vertex, which does not belong to any other hyperedges. Denote these vertices by  . Thus, a possible coprime labeling of the hypergraph
. Thus, a possible coprime labeling of the hypergraph  is represented by the following square array:
is represented by the following square array:
Suppose that the linear hypergraph 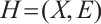 has x vertices. Clearly, we have
has x vertices. Clearly, we have  . Note that one is coprime to any other integers, and any prime between
. Note that one is coprime to any other integers, and any prime between  and
and 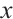 is coprime to the rest numbers of the square array. Therefore, in order to prove that the theorem holds, we only need to prove that
is coprime to the rest numbers of the square array. Therefore, in order to prove that the theorem holds, we only need to prove that  . By Lemma 2, we have that for
. By Lemma 2, we have that for  ,
, . Since
. Since , hence
, hence  . Furthermore, for
. Furthermore, for 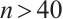 ,
,  . Thus
. Thus  . Let
. Let  , and
, and  be distinct primes between
be distinct primes between  and
and  . It is evident that Theorem 2 holds and the proof is complete.
. It is evident that Theorem 2 holds and the proof is complete.
Remark Erdös-Faber-Lovász conjectured that if the linear hypergraph  has
has  hyperedges and each hyperedge has
hyperedges and each hyperedge has  vertices, then there is a
vertices, then there is a  -vertex colour of the hypergraph such that each edge contains vertices of all colours[8]. Recently, Kang et al[8] proved that this conjecture holds for every large
-vertex colour of the hypergraph such that each edge contains vertices of all colours[8]. Recently, Kang et al[8] proved that this conjecture holds for every large  . Here, we prove that
. Here, we prove that  is prime. Based on our method, one can prove that when
is prime. Based on our method, one can prove that when  is an integer greater than 1, an
is an integer greater than 1, an  ×
× grid is a prime hypergraph. In fact, the
grid is a prime hypergraph. In fact, the  ×
× grid can be regarded as a linear hypergraph with
grid can be regarded as a linear hypergraph with  hyperedges (
hyperedges ( rows and
rows and  columns) and
columns) and  vertices. On one hand, we have that for
vertices. On one hand, we have that for  ,
,  , and for
, and for  ,
,  .On the other hand, denote those vertices in its principal diagonal by
.On the other hand, denote those vertices in its principal diagonal by  Let
Let  and
and  be distinct primes between
be distinct primes between 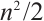 and
and  . Do the cases
. Do the cases  separately. This immediately confirms the previous assertion that a
separately. This immediately confirms the previous assertion that a  ×
×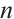 grid is a prime hypergraph.
grid is a prime hypergraph.
References
- Gallian J. A dynamic survey of graph labeling[EB/OL]. [2024-02-10]. https://www.combinatorics.org/files/Surveys/ds6/ds6v22-2019.pdf. [Google Scholar]
- Fu H L, Huang K C. On prime labellings[J]. Discrete Mathematics, 1994, 127(1/2/3): 181-186. [CrossRef] [MathSciNet] [Google Scholar]
- Pikhurko O. Trees are almost prime[J]. Discrete Mathematics, 2007, 307(11/12): 1455-1462. [CrossRef] [MathSciNet] [Google Scholar]
- Robertson L, Small B. On Newman's conjecture and prime trees[J]. Integers, 2009, 9(2): 117-128. [CrossRef] [MathSciNet] [Google Scholar]
- Haxell P, Pikhurko O, Taraz A. Primality of trees[J]. Journal of Combinatorics, 2011, 2(4): 481-500. [CrossRef] [MathSciNet] [Google Scholar]
- Pomerance C, Selfridge J L. Proof of D. J. Newman's coprime mapping conjecture[J]. Mathematika, 1980, 27(1): 69-83. [CrossRef] [MathSciNet] [Google Scholar]
- Rosser J B, Schoenfeld L. Approximate formulas for some functions of prime numbers[J]. Illinois Journal of Mathematics, 1962, 6(1): 64-94. [CrossRef] [MathSciNet] [Google Scholar]
- Kang D, Kelly T, Kühn D, et al. A proof of the Erdős-Faber-Lovász conjecture[J]. Annals of Mathematics, 2023, 198(2): 537-618. [CrossRef] [MathSciNet] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.







