| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 1, February 2025
|
|
|---|---|---|
| Page(s) | 60 - 68 | |
| DOI | https://doi.org/10.1051/wujns/2025301060 | |
| Published online | 12 March 2025 | |
Mathematics
CLC number: O177
Property
 and Property
and Property
 for Operator and Its Functions
for Operator and Its Functions
算子及算子函数的
 性质与
性质与
 性质
性质
1 School of Mathematics and Statistics, Weinan Normal University, Weinan 714099, Shaanxi, China
2 School of Mathematics and Statistics, Shaanxi Normal University, Xi'an 710062, Shaanxi, China
Received:
18
April
2024
By using the topological uniform descent, the necessary and sufficient conditions for which property  and property
and property  hold for bounded linear operators are given. As a consequence of the main result, the stability of property
hold for bounded linear operators are given. As a consequence of the main result, the stability of property  and property
and property  is studied, and a new judgement for operator functions that satisfy property
is studied, and a new judgement for operator functions that satisfy property  and property
and property  is discussed.
is discussed.
摘要
本文运用拓扑一致降标性质,给出了有界线性算子同时满足 性质与
性质与 性质的充要条件。之后利用主要结论,研究了
性质的充要条件。之后利用主要结论,研究了 性质与
性质与 性质的稳定性,并得到了算子函数同时有
性质的稳定性,并得到了算子函数同时有 性质与
性质与 性质的新判定方法。
性质的新判定方法。
Key words: property (WE) / property (R) / spectrum
关键字 : (WE)性质 / (R)性质 / 谱
Cite this article: SUN Chenhui, CAO Xiaohong. Property (WE) and Property (R) for Operator and Its Functions[J]. Wuhan Univ J of Nat Sci, 2025, 30(1): 60-68.
Biography: SUN Chenhui, female, Ph. D., Associate professor, research direction: operator theory. E-mail: sunchenhui1986@163. com
Foundation item: Supported by the 2021 General Special Scientific Research Project of the Education Department of Shaanxi Provincial Government (21JK0637), the Science and Technology Planning Project of Weinan Science and Technology Bureau (2022ZDYFJH-11) and the 2021 Talent Project of Weinan Normal University (2021RC16)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
The Weyl type theorem of bounded linear operator can well reflect the structure characteristics and distribution of operator's spectral[1-5]. Therefore, the Weyl type theorem is an important topic in spectral theory. In recent years, the research scope of Weyl type theorems has been extended from general operators to operator functions, operator matrices, etc. Numerous significant results have been obtained[6-9]. Property  and property
and property  are the latest variations of Weyl type theorems, which have attracted the attention and research of operator theorists[10-12]. In this paper, by decomposing and constructing the operator spectrum and using the topological uniform scaling property, we give a new method for bounded linear operators and operator functions to satisfy the property
are the latest variations of Weyl type theorems, which have attracted the attention and research of operator theorists[10-12]. In this paper, by decomposing and constructing the operator spectrum and using the topological uniform scaling property, we give a new method for bounded linear operators and operator functions to satisfy the property  and property
and property  . Furthermore, the perturbation of property
. Furthermore, the perturbation of property  and property
and property 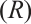 is characterized, and the necessary and sufficient conditions for the operator function to have both the property
is characterized, and the necessary and sufficient conditions for the operator function to have both the property  and property
and property  are studied.
are studied.
Throughout this paper,  denotes a complex separable infinite dimensional Hilbert space. Let
denotes a complex separable infinite dimensional Hilbert space. Let  be the algebra of all bounded linear operators on
be the algebra of all bounded linear operators on  . For an operator
. For an operator  we shall denote by
we shall denote by  the dimension of the kernel
the dimension of the kernel  , and by
, and by 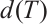 the codimension of the range
the codimension of the range  . We call
. We call  is an upper semi-Fredholm operator if
is an upper semi-Fredholm operator if  and
and  is closed. If
is closed. If  is an upper semi-Fredholm operator and
is an upper semi-Fredholm operator and  , we call
, we call  a bounded below operator. If
a bounded below operator. If 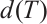
 ,
,  is a lower semi-Fredholm operator. An operator
is a lower semi-Fredholm operator. An operator  is said to be Fredholm if
is said to be Fredholm if  is closed and both
is closed and both  and
and  are finite. If
are finite. If  is an upper (or a lower) semi-Fredholm operator, the index of
is an upper (or a lower) semi-Fredholm operator, the index of  ,
,  , is defined to be
, is defined to be 
 . The ascent of
. The ascent of  ,
,  , is the least non-negative integer
, is the least non-negative integer  such that
such that 
 and the descent,
and the descent,  , is the least non-negative integer
, is the least non-negative integer  such that
such that 

 . We call
. We call  a Drazin invertible operator if
a Drazin invertible operator if 
 . The operator
. The operator  is Weyl if it is Fredholm of index zero, and
is Weyl if it is Fredholm of index zero, and  is said to be Browder if it is Fredholm "of finite ascent and descent". Let
is said to be Browder if it is Fredholm "of finite ascent and descent". Let  be the spectrum of
be the spectrum of  and
and  be the approximate point spectrum of
be the approximate point spectrum of  . We write
. We write  ,
,  ,
,  ,
, 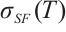 ,
,  and
and  for the Weyl spectrum of
for the Weyl spectrum of  , the Browder spectrum of
, the Browder spectrum of  , the essential spectrum of
, the essential spectrum of  , the semi-Fredholm spectrum of
, the semi-Fredholm spectrum of  , the essential approximate point spectrum of
, the essential approximate point spectrum of  and the Browder essential approximate point spectrum of
and the Browder essential approximate point spectrum of  . Let
. Let 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 (
( denotes the set of complex numbers).
denotes the set of complex numbers).  is called an isoloid operator if
is called an isoloid operator if 
 where
where 
 . For a set
. For a set 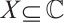 , we write
, we write  ,
,  and
and  for the set of isolated points, accumulation points and boundary points set of
for the set of isolated points, accumulation points and boundary points set of  . We denote by
. We denote by  the set of all normal eigenvalues of
the set of all normal eigenvalues of  , thus
, thus 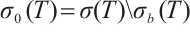 .
.  satisfies property
satisfies property  if
if  , where
, where 
 [10].
[10].  satisfies property
satisfies property  if
if  , where
, where  [10].
[10].
In this paper, we mainly study property  and property
and property  for bounded linear operators and its functions. Some meaningful conclusions are obtained.
for bounded linear operators and its functions. Some meaningful conclusions are obtained.
1 Judgement of Property  and Property
and Property  for Bounded Linear Operators
for Bounded Linear Operators
Although both property  and property
and property  are variations of Weyl's theorem based on their definitions, there is no necessary connection between them.
are variations of Weyl's theorem based on their definitions, there is no necessary connection between them.
Remark 1 (i)  satisfies property
satisfies property 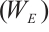

 satisfies property
satisfies property  .
.
Let 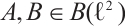 be defined by
be defined by  ,
,  . Suppose that
. Suppose that  . Then
. Then  ,
,  ,
,  ,
,  .
.  satisfies property
satisfies property  , but property
, but property  does not hold for
does not hold for  .
.
(ii)  satisfies property
satisfies property 

 satisfies property
satisfies property 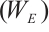 .
.
Let  be defined by
be defined by  ,
,  ,
,  . We have that
. We have that  ,
,  .
.  . So
. So  satisfies property
satisfies property  and
and  does not have property
does not have property  .
.
(iii) 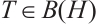 has property
has property  and property
and property 
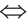
 and
and  .
.
Topological uniform descent is an important property of operators, which is widely used in spectral theory. If  , then for each nonnegative integer
, then for each nonnegative integer  ,
,  induces a linear transformation from the vector space
induces a linear transformation from the vector space  to
to  . We denote
. We denote  the dimension of the null space of the induced map and let
the dimension of the null space of the induced map and let  . The following definition was introduced by Grabiner[13]. Let
. The following definition was introduced by Grabiner[13]. Let  , if there is a nonnegative integer
, if there is a nonnegative integer  for which
for which  for
for  and
and  is closed in the operator range topology of
is closed in the operator range topology of  for
for  , then we say that
, then we say that  has topological uniform descent.
has topological uniform descent.
It can be shown that if  is upper semi-Fredholm, then
is upper semi-Fredholm, then  has topological uniform descent. Let
has topological uniform descent. Let  has topological uniform descent},
has topological uniform descent}, 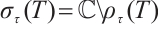 . Grabiner discovered many properties of topological uniform descent. We will use the following property (Ref. [13], Corollary 4.9): Suppose that
. Grabiner discovered many properties of topological uniform descent. We will use the following property (Ref. [13], Corollary 4.9): Suppose that  ,
,  , if
, if  has topological uniform descent, then
has topological uniform descent, then  is a pole of
is a pole of  . Next, we will discuss property
. Next, we will discuss property 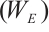 and property
and property  by using the topological uniform descent.
by using the topological uniform descent.
Lemma 1 Let  , the following statements are equivalent:
, the following statements are equivalent:
(1)  satisfies property
satisfies property  ;
;
(2)  ;
;
(3) 
Proof (1) (2). Suppose that
(2). Suppose that  satisfies property
satisfies property  . If
. If 
 , then there exists a deleted neighborhood
, then there exists a deleted neighborhood  centered on
centered on  such that for any
such that for any  ,
,  is a Weyl operator. Since
is a Weyl operator. Since 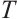 has property
has property 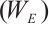 , we know that
, we know that 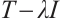 is a Browder operator. Then we get that
is a Browder operator. Then we get that  . We assume that
. We assume that  . If
. If  , we get that
, we get that  is Drazin invertible. According to
is Drazin invertible. According to  , we have
, we have  . Since
. Since  satisfies property
satisfies property  , we can get that
, we can get that  is a Browder operator. If
is a Browder operator. If  , we can also get that
, we can also get that  and
and 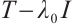 is Browder operators. The inclusion "
is Browder operators. The inclusion " " is obviously true.
" is obviously true.
(2) (1). Since
(1). Since  and
and 
 , we know that
, we know that  . Similarly,
. Similarly, 
 . Hence
. Hence  satisfies property
satisfies property  .
.
The fact that 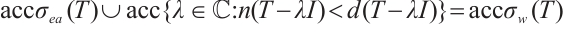 implies that (2)
implies that (2) (3).
(3).
The closeness of operator range is very important in spectral theory. According to the closeness of operator range, the following spectral set is defined:  is not closed}.
is not closed}.
Lemma 2 Let  , the following statements are equivalent:
, the following statements are equivalent:
(1)  satisfies property
satisfies property  ;
;
(2) 
 ;
;
(3) 
Proof (1) (2). Suppose
(2). Suppose 
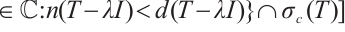 . Without loss of generality, we assume that
. Without loss of generality, we assume that  . Then we have
. Then we have  . There exists a deleted neighborhood
. There exists a deleted neighborhood  centered on
centered on  such that for any
such that for any  ,
,  . If
. If  , then
, then  . Since
. Since  satisfies property
satisfies property  , we have that
, we have that  is a Browder operator. Suppose that
is a Browder operator. Suppose that  , if
, if  , then
, then  is an upper semi-Fredholm operator. By
is an upper semi-Fredholm operator. By  ,
,  and
and  , we know that
, we know that  . Because
. Because  has property
has property  , we can get that
, we can get that  . If
. If  , then exists a deleted neighborhood
, then exists a deleted neighborhood  centered on
centered on  such that for any
such that for any  ,
,  . Therefore
. Therefore  . Since
. Since  and
and  , we can also get that
, we can also get that  .
.
(2) (1). Suppose that
(1). Suppose that  . It follows that
. It follows that 
 . So
. So  is a Browder operator. Then we have
is a Browder operator. Then we have  . Similarly, we can get the inclusion "
. Similarly, we can get the inclusion " ". Hence
". Hence  satisfies property
satisfies property  .
.
If (2) holds, then  has property
has property  . This implies that
. This implies that  , where
, where  . It follows that
. It follows that 
 . Hence
. Hence 

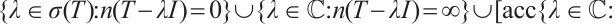

 . Then we have that
. Then we have that 
The inclusion " " is obviously true. This implies that (3) holds. For the converse, if (3) holds, by
" is obviously true. This implies that (3) holds. For the converse, if (3) holds, by  we know that (2) holds. Therefore (2)
we know that (2) holds. Therefore (2) (3).
(3).
Based on Lemma 1 and Lemma 2, the following results demonstrate that the two properties can be valid at the same time:
Theorem 1
 satisfies property
satisfies property  and property
and property  if and only if
if and only if 
Proof " ". Suppose
". Suppose  has property
has property  . Using Lemma 2, we have that
. Using Lemma 2, we have that  Since
Since  has property
has property  , we know that
, we know that  Thus
Thus 
" ". By the condition, we get that
". By the condition, we get that  The inclusion "
The inclusion " " is obviously true. From Lemma 2, we know that
" is obviously true. From Lemma 2, we know that  satisfies property
satisfies property  .
.
If  , then
, then  is a Browder operator,
is a Browder operator,  . The converse is similar. Therefore
. The converse is similar. Therefore  satisfies property
satisfies property 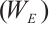 .
.
Remark 2 (i) In Theorem 1, suppose  satisfies property
satisfies property  and property
and property  , then each part of the decomposition of
, then each part of the decomposition of  cannot be deleted.
cannot be deleted.
( ) Let
) Let  be defined by
be defined by  . Hence
. Hence  has property
has property  and property
and property  . But
. But  Thus
Thus  cannot be deleted.
cannot be deleted.
( ) Let
) Let  be defined by
be defined by  . Then
. Then  has property
has property  and property
and property  . But
. But 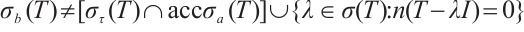

 . Thus
. Thus  cannot be deleted.
cannot be deleted.
( ) Let
) Let  be defined by
be defined by  . We know that
. We know that  has property
has property  and property
and property  . But
. But 

 . Hence
. Hence  cannot be deleted.
cannot be deleted.
( ) Let
) Let  be defined by
be defined by  ,
, 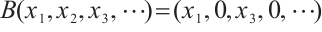 . And suppose
. And suppose  . Then
. Then  satisfies property
satisfies property 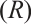 and property
and property  . But
. But 



 . Therefore
. Therefore  cannot be deleted.
cannot be deleted.
( ) Let
) Let  be defined by
be defined by  ,
, 
 . And suppose
. And suppose  . Thus
. Thus  satisfies property
satisfies property  and property
and property  . But
. But 



 . It follows that
. It follows that  cannot be deleted.
cannot be deleted.
(ii) The conditions in Theorem 1 can be transformed as follows:  can be replaced by
can be replaced by  ,
,  can be replaced by
can be replaced by  .
.
From Lemma 1 and Lemma 2, we can get the following Corollary.
Corollary 1 Let  . Then:
. Then:
(1)  satisfies property
satisfies property 




 ;
;
(2)  satisfies property
satisfies property
By Theorem 1 and Corollary 1, we can get the following Corollary.
Corollary 2 Let  . Then
. Then  satisfies property
satisfies property  and property
and property 
Proof Using Theorem 1,  satisfies property
satisfies property  and property
and property 
" ".
".  is obvious. If
is obvious. If 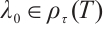 and
and 
 , by Theorem 1 we know that
, by Theorem 1 we know that  .
.
" ". Suppose
". Suppose  and
and 
 . If
. If  , we have
, we have  by the condition. Suppose
by the condition. Suppose  , if
, if  , we can get that
, we can get that  , then
, then  is a Browder operator. If
is a Browder operator. If  , using
, using  we have
we have  . It also follows that
. It also follows that  . From Theorem 1, we can get that
. From Theorem 1, we can get that  satisfies property
satisfies property  and property
and property  .
.
2 The Perturbation of Property 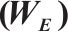 and Property
and Property 
Suppose  satisfies property
satisfies property  or property
or property  and
and  is a compact operator or even a finite rank operator, but we cannot deduce that
is a compact operator or even a finite rank operator, but we cannot deduce that  satisfies property
satisfies property  or property
or property  . For example, let
. For example, let  be defined by
be defined by  ,
, 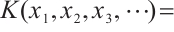
 . It is obviously that
. It is obviously that  satisfies property
satisfies property  and property
and property  and
and  is a finite rank operator. However, calculations indicate that
is a finite rank operator. However, calculations indicate that  does not satisfy either property
does not satisfy either property  or property
or property  .
.
The operator  is called a power finite rank operator, if there is a positive integer
is called a power finite rank operator, if there is a positive integer  such that
such that  . A power finite rank operator is a Riesz operator, therefore, when
. A power finite rank operator is a Riesz operator, therefore, when  is a power finite rank operator, operator
is a power finite rank operator, operator  is commutative with
is commutative with  , then it has the following properties:
, then it has the following properties:  , where
, where 
 and
and  [14].
[14].
Due to the complexity of general compact perturbations, this section focuses on the power finite rank perturbation of property  and property
and property  .
.
Lemma 3 Let  and
and  is a power finite rank operator with
is a power finite rank operator with  . The following statements are equivalent:
. The following statements are equivalent:
(1)  satisfies property
satisfies property  and is an isoloid operator;
and is an isoloid operator;
(2)  ;
;
(3)  .
.
Proof (1) (2). Since
(2). Since  satisfies property
satisfies property  and
and 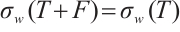 ,
, 
 , we have that
, we have that  . If
. If  , when
, when  , by the proof of Lemma 1, we know that
, by the proof of Lemma 1, we know that  is Drazin invertible. Thus
is Drazin invertible. Thus  . If
. If  , then
, then  . Since
. Since  has property
has property  , we get that
, we get that  is a Browder operator. It is a contradiction. Therefore
is a Browder operator. It is a contradiction. Therefore  , hence
, hence  . By
. By  is Drazin invertible we have that
is Drazin invertible we have that  . Suppose that
. Suppose that  . Without loss of generality, we assume that
. Without loss of generality, we assume that  . Then
. Then  . The fact that
. The fact that  is isoloid implies that
is isoloid implies that  . Because
. Because  has the property
has the property  ,
,  is a Browder operator. We also have that
is a Browder operator. We also have that  .
.
(2) (1). Suppose that
(1). Suppose that  . Then we have that
. Then we have that  is a Weyl operator. So
is a Weyl operator. So  . By condition (2), we can get that
. By condition (2), we can get that  is a Browder operator. Thus
is a Browder operator. Thus  is a Browder operator. Then
is a Browder operator. Then  . Contrarily, if
. Contrarily, if  , then
, then 
 . Therefore
. Therefore  . Hence
. Hence  and
and  are Browder operators.
are Browder operators.
If there exists  such that
such that  , then
, then  . By condition (2), we have that
. By condition (2), we have that  is a Browder operator. It follows that
is a Browder operator. It follows that  is a Browder operator. The fact that
is a Browder operator. The fact that  implies that
implies that  is invertible, which is a contradiction. Therefore
is invertible, which is a contradiction. Therefore  is an isoloid operator.
is an isoloid operator.
(1) (3). Suppose
(3). Suppose 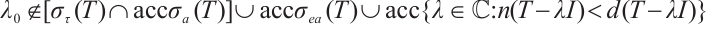 . If
. If  , from the proof of (1)
, from the proof of (1)  (2) we can get that
(2) we can get that  . If
. If 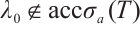 , we assume that
, we assume that  without loss of generality. Since
without loss of generality. Since  , we have that
, we have that  . Hence
. Hence  . Since
. Since  is isoloid and satisfies property
is isoloid and satisfies property  , we have that
, we have that  is a Browder operator. Thus
is a Browder operator. Thus  .
.
(3) (1). The proof for (3)
(1). The proof for (3) (1) is the same as the proof for (2)
(1) is the same as the proof for (2) (1).
(1).
Lemma 4 Let  and
and  is a power finite rank operator with
is a power finite rank operator with  . The following statements are equivalent:
. The following statements are equivalent:
(1)  is an isoloid operator and satisfies property
is an isoloid operator and satisfies property  ,
,  ;
;
(2)  ;
;
(3) 
Proof (1) (2). Suppose
(2). Suppose 
 . We assume that
. We assume that  . If
. If 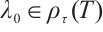 , when
, when  , we can get that
, we can get that  . Then
. Then  is a Browder operator. When
is a Browder operator. When  , we have that
, we have that  is a Weyl operator. Hence
is a Weyl operator. Hence  . The fact that
. The fact that  satisfies property
satisfies property  implies that
implies that  is a Browder operator. Hence
is a Browder operator. Hence  . If
. If 
 , then
, then  . We can assume that
. We can assume that  . Since
. Since  is an isoloid operator, we have that
is an isoloid operator, we have that  . Since
. Since  satisfies property
satisfies property 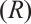 , we can get that
, we can get that  is a Browder operator. Therefore
is a Browder operator. Therefore  .
.
(2) (1). Let's first prove that
(1). Let's first prove that  is an isoloid operator. If there exists
is an isoloid operator. If there exists  such that
such that  . We assume that
. We assume that  without loss of generality. Thus
without loss of generality. Thus  ,
,  . Therefore
. Therefore 
 . It follows that
. It follows that  is a Browder operator. Then
is a Browder operator. Then  is a Browder operator. Hence
is a Browder operator. Hence  is invertible, which is a contradiction. Thus
is invertible, which is a contradiction. Thus  is an isoloid operator.
is an isoloid operator.
Next we will prove 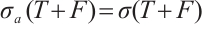 . If
. If  , then
, then 
 . It implies that both
. It implies that both  and
and  are Browder operators. Hence
are Browder operators. Hence  .
.
If  , then
, then 
 . Hence
. Hence  and
and  are Browder operators. Thus
are Browder operators. Thus  . Conversely, suppose that
. Conversely, suppose that  , then
, then  . Then we also have that
. Then we also have that 

 . Thus
. Thus  and
and  are Browder operators. Hence
are Browder operators. Hence  satisfies property
satisfies property  .
.
The proof for (1) (3) is the same as the proof for (1)
(3) is the same as the proof for (1) (2).
(2).
Then we obtain the finite rank perturbation with two properties held at the same time.
Theorem 2 Let  and
and  is a power finite rank operator with
is a power finite rank operator with  . The following statements are equivalent:
. The following statements are equivalent:
(1)  is an isoloid operator and satisfies property
is an isoloid operator and satisfies property  and property
and property  ,
, 
 ;
;
(2) 
Proof (1) (2). Suppose
(2). Suppose 
 . If
. If  , by Lemma 4 we have that
, by Lemma 4 we have that  . If
. If  , by Lemma 3 we also get that
, by Lemma 3 we also get that  .
.
(2) (1). The statement (2) implies that
(1). The statement (2) implies that  . Suppose
. Suppose 
 , then
, then 
 . If
. If  , then
, then 
 . If
. If  , we have that
, we have that  . Thus
. Thus  is Drazin invertible. Therefore
is Drazin invertible. Therefore 
 . Hence
. Hence 


 . Then
. Then  is a Browder operator. Thus
is a Browder operator. Thus 
 . With Lemma 3 we get that
. With Lemma 3 we get that  is isoloid and satisfies property
is isoloid and satisfies property  .
.
By condition (2) we have that 

 . Then according to Lemma 4 we have that
. Then according to Lemma 4 we have that  satisfies property
satisfies property  and
and  . Therefore (1) holds.
. Therefore (1) holds.
3 Property  and Property
and Property  for Operator Functions
for Operator Functions
Let  be the class of all complex-valued functions which are analytic on a neighborhood of
be the class of all complex-valued functions which are analytic on a neighborhood of  and are not constant on any component of
and are not constant on any component of  . For the function's properties, we discuss property
. For the function's properties, we discuss property  first.
first.
Lemma 5 Let  . For any
. For any  ,
,  satisfies property
satisfies property  if and only if
if and only if  ,
,  ,
,  and one of the following conditions holds:
and one of the following conditions holds:
(1)  ;
;
(2)  .
.
Proof " ". Suppose (1) holds. Then
". Suppose (1) holds. Then  ,
,  , thus for any
, thus for any  ,
,  ,
,  . Since
. Since 
 , we have that
, we have that  . So
. So  satisfies property
satisfies property  . If (2) holds, then
. If (2) holds, then 
 ,
,  . Hence
. Hence  . It follows that
. It follows that  . For the converse, let
. For the converse, let  , and let
, and let 
 , where
, where  , and
, and  is inverse. We assume that
is inverse. We assume that  , then
, then 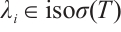 , thus
, thus  . It follows that
. It follows that  is a Browder operator.
is a Browder operator.
" ". If there exists
". If there exists  such that
such that  ,
,  , suppose that
, suppose that  , then
, then  . By
. By  satisfies property
satisfies property  , we have that
, we have that  is a Browder operator. Hence both
is a Browder operator. Hence both  and
and  are Browder operators. It is a contradiction. Thus
are Browder operators. It is a contradiction. Thus  ,
,  .
.
If  , then the fact that
, then the fact that  satisfies property
satisfies property  implies that
implies that  ,
,  . According to Lemma 1, we can get (1) holds. When
. According to Lemma 1, we can get (1) holds. When  , we can assert that
, we can assert that 
 . If not, suppose that
. If not, suppose that  ,
,  . Let
. Let  , then
, then  . Since
. Since  satisfies property
satisfies property  , then
, then  is a Browder operator, so is
is a Browder operator, so is  , which is a contradiction. Therefore
, which is a contradiction. Therefore  . By Lemma 1 and its proof, we get that (2) holds.
. By Lemma 1 and its proof, we get that (2) holds.
Similarly, we can obtain the following conclusion. Let  , for any
, for any  ,
,  satisfies property
satisfies property  if and only if
if and only if  ,
,  and one of the following conditions holds:
and one of the following conditions holds:
(1) 
 ;
;
(2)  .
.
Corollary 3 Let  , for any
, for any  ,
,  satisfies property
satisfies property  if and only if
if and only if  ,
,  and the following conditions holds:
and the following conditions holds:
(1) 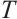 satisfies property
satisfies property  ;
;
(2) If  , then
, then  .
.
For property  of operator functions, we have the following conclusions.
of operator functions, we have the following conclusions.
Lemma 6 Let  , for any
, for any  ,
,  satisfies property
satisfies property  if and only if one of the following conditions holds:
if and only if one of the following conditions holds:
(1) 
 ;
;
(2)  .
.
Proof " ". If
". If  , then
, then  . By Lemma 2, we can get that (1) holds.
. By Lemma 2, we can get that (1) holds.
If  , we can assert that
, we can assert that  . If not, suppose that
. If not, suppose that  ,
,  , let
, let  , then
, then  . Since
. Since  satisfies property
satisfies property  , we can get that
, we can get that  is a Browder operator. Then
is a Browder operator. Then  is a Browder operator, which is a contradiction. Therefore
is a Browder operator, which is a contradiction. Therefore  . Similarly, we have
. Similarly, we have  in this situation. Suppose that
in this situation. Suppose that  . If
. If 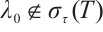 , by
, by  satisfies property
satisfies property  and
and  we have that
we have that  . The fact that
. The fact that  implies that
implies that  is a Browder operator. If
is a Browder operator. If  , we can assume that
, we can assume that  . Since
. Since 
 , we have
, we have  . By
. By  has property
has property  , we can get that
, we can get that  is a Browder operator. Therefore (2) holds.
is a Browder operator. Therefore (2) holds.
" ". If condition (1) holds, then
". If condition (1) holds, then  ,
,  ,
,  . Then for any
. Then for any 
 ,
,  . Hence
. Hence  . Since
. Since  , we have that
, we have that  . Therefore
. Therefore  satisfies property
satisfies property  .
.
If conditions (2) holds, then  ,
,  ,
, 
 . Hence
. Hence  . Suppose that
. Suppose that  . Let
. Let 
 , where
, where  ,
,  is invertible. We can assume that
is invertible. We can assume that  , then
, then  . Since
. Since  has property
has property  , we get
, we get  . So
. So 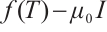 is a Browder operator. Therefore
is a Browder operator. Therefore  satisfies property
satisfies property  .
.
By the proof of Lemma 6, we can get that:
Corollary 4 Let  . For any
. For any  ,
,  satisfies property
satisfies property  if and only if the following conditions holds:
if and only if the following conditions holds:
(1)  satisfies property
satisfies property  ;
;
(2) If  , then
, then  .
.
Then we obtain the condition that the operator function satisfies both two properties.
Theorem 3 Let  . For any
. For any  ,
,  satisfies property
satisfies property  and property
and property  if and only if
if and only if  ,
,  and:
and:
(1)  satisfies property
satisfies property  and property
and property  ;
;
(2) If  , then
, then  .
.
Proof " ". According to Corollary 3 and Corollary 4, we know that we only need to prove (2). Suppose that
". According to Corollary 3 and Corollary 4, we know that we only need to prove (2). Suppose that  . If
. If  , by Corollary 3 we know that
, by Corollary 3 we know that  is a Browder operator. Suppose
is a Browder operator. Suppose  . When
. When  , by Corollary 4 we can get that
, by Corollary 4 we can get that  . When
. When  , the fact that
, the fact that  implies
implies  . Thus
. Thus  . We also get that
. We also get that  is a Browder operator. The converse is obviously true. Hence (2) holds.
is a Browder operator. The converse is obviously true. Hence (2) holds.
The sufficiency is easy to get from Corollary 3 and Corollary 4.
Corollary 5 Let  . For any
. For any  ,
,  satisfies property
satisfies property  and property
and property  if and only if
if and only if 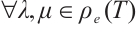 ,
,  and one of the following conditions holds:
and one of the following conditions holds:
(1) 

 ;
;
(2)  .
.
Proof " ". If
". If  , then
, then  . Since
. Since 
 , by Theorem 1 and Remark 2 we can get that (1) holds. If
, by Theorem 1 and Remark 2 we can get that (1) holds. If  , the condition (2) hold.
, the condition (2) hold.
" ". According to Theorem 1 and Theorem 3, we know that for any
". According to Theorem 1 and Theorem 3, we know that for any  ,
,  satisfies property
satisfies property  and property
and property  .
.
Example 1 Let  be defined by:
be defined by:  ,
, 
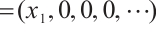 . Suppose that
. Suppose that  . Then: (1)
. Then: (1)  satisfies property
satisfies property  and property
and property  ; (2) For any
; (2) For any  ,
,  ; (3)
; (3)  , and
, and  .
.
Therefore by Theorem 3, we can get that for any  ,
,  satisfies property
satisfies property  and property
and property 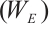 .
.
References
- Djordjević D S. Operators obeying a-Weyl's theorem[J]. Publicationes Mathematicae Debrecen, 1999, 55(3/4): 283-298. [CrossRef] [MathSciNet] [Google Scholar]
- Cao X H, Guo M Z, Meng B. Weyl spectra and Weyl's theorem[J]. Journal of Mathematical Analysis and Applications, 2003, 288(2): 758-767. [CrossRef] [MathSciNet] [Google Scholar]
- Gupta A, Kumar A. Properties (BR) and (BgR) for bounded linear operators[J]. Rendiconti Del Circolo Matematico Di Palermo Series 2, 2020, 69(2): 601-611. [CrossRef] [MathSciNet] [Google Scholar]
- Sun C H, Wang N, Cao X H. Topological uniform descent and judgement of a-Weyl's theorem [J]. Wuhan University Journal of Natural Sciences, 2023, 28(5): 392-398. [CrossRef] [EDP Sciences] [Google Scholar]
- Aiena P, Triolo S. Weyl-type theorems on Banach spaces under compact perturbations[J]. Mediterranean Journal of Mathematics, 2018, 15(3): 126. [CrossRef] [Google Scholar]
- Wu X F, Huang J J, Chen A. Weylness of 2 × 2 operator matrices[J]. Mathematische Nachrichten, 2018, 291(1): 187-203. [CrossRef] [MathSciNet] [Google Scholar]
- Dong J, Cao X H, Dai L. On weyl's theorem for functions of operators[J]. Acta Mathematica Sinica, English Series, 2019, 35(8): 1367-1376. [CrossRef] [MathSciNet] [Google Scholar]
- Dai L, Yi J L. Property (ω) and Hypercyclic Property for Operators[J]. Wuhan University Journal of Natural Sciences, 2024, 29(6): 499-507. [CrossRef] [EDP Sciences] [Google Scholar]
- Zhu S, Li C G, Zhou T T. Weyl type theorems for functions of operators [J]. Glasgow Mathematical Journal, 2012, 54(3): 493-505. [CrossRef] [MathSciNet] [Google Scholar]
- Berkani M, Kachad M. New Browder and weyl type theorems[J]. Bulletin of the Korean Mathematical Society, 2015, 52(2): 439-452. [CrossRef] [MathSciNet] [Google Scholar]
- Yang L L, Cao X H. Property (R) for functions of operators and its perturbations[J]. Mediterranean Journal of Mathematics, 2022, 19(1): 25. [CrossRef] [Google Scholar]
-
Ren Y X, Jiang L N, Kong Y Y. Property
 and topological uniform descent [J]. Bulletin of the Belgian Mathematical Society - Simon Stevin, 2022, 29(1): 1-17.
[MathSciNet]
[Google Scholar]
and topological uniform descent [J]. Bulletin of the Belgian Mathematical Society - Simon Stevin, 2022, 29(1): 1-17.
[MathSciNet]
[Google Scholar]
- Grabiner S. Uniform ascent and descent of bounded operators[J]. Journal of the Mathematical Society of Japan, 1982, 34(2): 317-337. [CrossRef] [MathSciNet] [Google Scholar]
- Rakočević V. Semi-Browder operators and perturbations[J]. Studia Mathematica, 1997, 122(2): 131-137. [CrossRef] [MathSciNet] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.