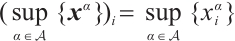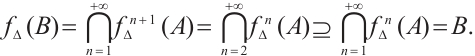| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 1, February 2025
|
|
|---|---|---|
| Page(s) | 43 - 48 | |
| DOI | https://doi.org/10.1051/wujns/2025301043 | |
| Published online | 12 March 2025 | |
Mathematics
CLC number: O19
Birkhoff Orbits for Twist Homeomorphisms on the High-Dimensional Cylinder
高维柱面上的扭转同胚的 Birkhoff 轨道
School of Mathematical Sciences, Suzhou University of Science and Technology, Suzhou 215009, Jiangsu, China
Received:
28
January
2024
It is known that monotone recurrence relations can induce a class of twist homeomorphisms on the high-dimensional cylinder, which is an extension of the class of monotone twist maps on the annulus or two-dimensional cylinder. By constructing a bounded solution of the monotone recurrence relation, the main conclusion in this paper is acquired: The induced homeomorphism has Birkhoff orbits provided there is a compact forward-invariant set. Therefore, it generalizes Angenent's results in low-dimensional cases.
摘要
单调回复关系可以诱导一族高维柱面上的扭转同胚,它们是环域或二维柱面上单调扭转映射的推广。本文通过构造单调回复关系的有界解,获得如下的主要结论:如果诱导同胚有一个紧致的正向不变集,那么它有 Birkhoff 轨道。因此,本文推广了 Angenent 在低维情形的结果。
Key words: monotone recurrence relation / twist homeomorphism / high-dimensional cylinder / bounded action / Birkhoff orbit
关键字 : 单调回复关系 / 扭转同胚 / 高维柱面 / 有界作用 / Birkhoff轨道
Cite this article: ZHOU Tong. Birkhoff Orbits for Twist Homeomorphisms on the High-Dimensional Cylinder[J]. Wuhan Univ J of Nat Sci, 2025, 30(1): 43-48.
Biography: ZHOU Tong, male, Ph. D., Lecturer, research direction: dynamical systems. E-mail: zhoutong@mail.usts.edu.cn
Foundation item: Supported by the National Natural Science Foundation of China (12201446), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (22KJB110005), and the Shuangchuang Program of Jiangsu Province (JSSCBS20220898)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
For monotone twist maps on the annulus or two-dimensional cylinder, one important study object is the order-preserving orbits which are special orbits with rotation numbers. These orbits are usually called Birkhoff orbits[1-4].
There are many results related to the existence of Birkhoff orbits for twist maps in the past few decades. Hall's result[3] stated that if there is a  -periodic orbit, then there exists a Birkhoff
-periodic orbit, then there exists a Birkhoff  -periodic orbit. Furthermore, the Aubry-Mather theorem[4-6] tells us that each
-periodic orbit. Furthermore, the Aubry-Mather theorem[4-6] tells us that each  in the twist interval of an area-preserving twist diffeomorphism can be realized by a Birkhoff orbit.
in the twist interval of an area-preserving twist diffeomorphism can be realized by a Birkhoff orbit.
The main topic of this paper is to show the existence of Birkhoff orbits for twist homeomorphisms on the high-dimensional cylinder. For this purpose, we recall the definition of monotone recurrence relations of type  [1] as follows:
[1] as follows:
where  and
and  satisfies
satisfies
(H1)  is a nondecreasing function of all the
is a nondecreasing function of all the  except
except  . Moreover, it is strictly increasing in
. Moreover, it is strictly increasing in  and
and  ,
,
(H2)  ,
,
(H3)  and
and 
We say  is a solution of (1) if it satisfies (1). Solutions of (1) will generate a dynamical system on the high-dimensional cylinder[1]. In fact, monotone recurrence relation (1) can determine by (H1) and (H3) a homeomorphism
is a solution of (1) if it satisfies (1). Solutions of (1) will generate a dynamical system on the high-dimensional cylinder[1]. In fact, monotone recurrence relation (1) can determine by (H1) and (H3) a homeomorphism  in the following way:
in the following way:  is a solution of (1) if and only if
is a solution of (1) if and only if
Taking (H2) into account, (1) defines a homeomorphism  . Therefore, we obtain the twist homeomorphism on the high-dimensional cylinder, a generalization of the classical monotone twist map on the two-dimensional cylinder. Because of the one-to-one correspondence between solutions of (1) and orbits of
. Therefore, we obtain the twist homeomorphism on the high-dimensional cylinder, a generalization of the classical monotone twist map on the two-dimensional cylinder. Because of the one-to-one correspondence between solutions of (1) and orbits of  , we may study orbits of
, we may study orbits of  according to solutions of (1).
according to solutions of (1).
For a subclass of monotone recurrence relations, we remark that the existence of Birkhoff solutions (see Definition 1) of (1), corresponding to the existence of Birkhoff orbits of  , has been very clear. We give a brief exposition of this kind of monotone recurrence relations. Let
, has been very clear. We give a brief exposition of this kind of monotone recurrence relations. Let  be a positive integer indicating the range of interactions between particles and
be a positive integer indicating the range of interactions between particles and  be a
be a  function satisfying the following conditions[7-10]:
function satisfying the following conditions[7-10]:
(C1) 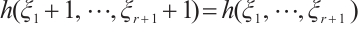 ;
;
(C2)  is bounded from below and
is bounded from below and 
 if
if  ;
;
(C3) Twist condition:
and
Let the Lagrangian  denote the energy of a system of particles, that is,
denote the energy of a system of particles, that is,
Then a variational monotone recurrence relation is defined by finding a stationary point of  :
:
We denote  then
then 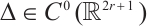 satisfies (H1)-(H3) due to (C1)-(C3), and (2) is equivalent to
satisfies (H1)-(H3) due to (C1)-(C3), and (2) is equivalent to
We call (3) the monotone recurrence relation generated by  or the variational monotone recurrence relation. It follows from the Aubry-Mather theory[11,12] that for each
or the variational monotone recurrence relation. It follows from the Aubry-Mather theory[11,12] that for each  , there exist Birkhoff minimizers (Birkhoff minimal solutions) with rotation number
, there exist Birkhoff minimizers (Birkhoff minimal solutions) with rotation number 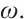 We emphasize that (3) corresponds to a conservative system. However, there exist a large number of non-conservative systems which could not be generated by such type of
We emphasize that (3) corresponds to a conservative system. However, there exist a large number of non-conservative systems which could not be generated by such type of  For instance, we consider the dissipative system:
For instance, we consider the dissipative system:
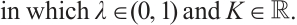 It is easy to check that (4) is a monotone recurrence relation satisfying (H1)-(H3), but it could not be generated by any
It is easy to check that (4) is a monotone recurrence relation satisfying (H1)-(H3), but it could not be generated by any  function
function  satisfying (C1)-(C3) (see Section 4).
satisfying (C1)-(C3) (see Section 4).
For general monotone recurrence relation (1), we can not utilize the Aubry-Mather theory because of the loss of the variational structure. Therefore, it would be interesting to investigate by a new method the existence of Birkhoff orbits for general  induced by (1).
induced by (1).
We review relevant results for general systems (not necessarily conservative) obtained in low-dimensional cases. Angenent[1] proved that a circle endomorphism with degree one must have a Birkhoff orbit, and for the two-dimensional case, he[1] demonstrated that if there exists  such that the twist homeomorphism (without the area-preserving assumption) maps
such that the twist homeomorphism (without the area-preserving assumption) maps  into itself, then the twist homeomorphism has a Birkhoff orbit.
into itself, then the twist homeomorphism has a Birkhoff orbit.
In this paper, we present the following criterion for the existence of Birkhoff orbits, which is a high-dimensional extension of previous results.
Theorem 1 If there exists a compact forward-invariant set 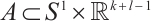 for
for  , then
, then  has a Birkhoff orbit.
has a Birkhoff orbit.
We stress that we are dealing with high-dimensional cases and our approach here is quite different. To obtain Theorem 1, one crucial step is to construct a compact invariant set for  , which helps us to obtain the orbits with bounded action in "two directions".
, which helps us to obtain the orbits with bounded action in "two directions".
1 Preliminaries
We denote  equipped with the product topology by
equipped with the product topology by  and
and  , where
, where  denotes the configuration with all components being
denotes the configuration with all components being  . Because of the periodicity hypothesis (H2), we often consider solutions of (1) in
. Because of the periodicity hypothesis (H2), we often consider solutions of (1) in  .
.
Let  and
and  be a lift of
be a lift of  . We define
. We define
which is independent of the lift  .
.
The space  is partially ordered by
is partially ordered by
1)  if and only if
if and only if  for all
for all  ;
;
2)  if and only if
if and only if  and
and  ;
;
3)  if and only if
if and only if  for all
for all  .
.
We say a configuration  has rotation number
has rotation number  , if the limit
, if the limit 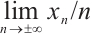 exists and it equals to
exists and it equals to  . We call
. We call  a configuration with bounded action[8] if there is a constant
a configuration with bounded action[8] if there is a constant  such that
such that  for all
for all  .
.
We remark that a configuration with bounded action and a configuration with rotation number are two independent concepts. To be precise, on the one hand, a configuration with bounded action is not necessarily a configuration with rotation number. For example,  . On the other hand, a configuration with rotation number is not necessarily a configuration with bounded action. For example,
. On the other hand, a configuration with rotation number is not necessarily a configuration with bounded action. For example, 
We define a family of order-preserving homeomorphisms  on
on  :
:
The action of  on
on  can be described as shifting
can be described as shifting  to the right by
to the right by  and shifting it up by
and shifting it up by  .
.
The left-shift operator  is defined by
is defined by  , where
, where  is a lift of
is a lift of  . If we denote
. If we denote  to be the set of solutions of (1), then the system generated by
to be the set of solutions of (1), then the system generated by  on
on  is equivalent to that by
is equivalent to that by  on the high-dimensional cylinder.
on the high-dimensional cylinder.
Let  be a solution of (1) with bounded action. We consider the closure of the set of translates of
be a solution of (1) with bounded action. We consider the closure of the set of translates of  :
:
Lemma 1 The set  is compact and
is compact and  -invariant.
-invariant.
Proof It is clear that  is
is 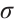 -invariant. It suffices to show
-invariant. It suffices to show  is compact. Let
is compact. Let  with
with  be a lift of
be a lift of  and
and  be the projection from
be the projection from  to
to  Then
Then  . Since
. Since  is a solution of (1) with bounded action, there exists
is a solution of (1) with bounded action, there exists  independent of
independent of  such that
such that
A simple calculation gives that  , where
, where  and
and  Thus we have
Thus we have 

 . It follows from Tychonoff's theorem that
. It follows from Tychonoff's theorem that  is compact, and therefore
is compact, and therefore  is compact. Moreover,
is compact. Moreover,
We come to the conclusion that  is compact.
is compact.
Definition 1 We say a configuration  is Birkhoff, if for any
is Birkhoff, if for any  ,
,  , or
, or  .
.
Let  denote the set of Birkhoff configurations. It is easy to see that
denote the set of Birkhoff configurations. It is easy to see that  is closed in the product topology and
is closed in the product topology and  for all
for all  . Moreover, Birkhoff configurations possess the following property.
. Moreover, Birkhoff configurations possess the following property.
Proposition 1[1,2,13] If  is Birkhoff, then
is Birkhoff, then  has a rotation number
has a rotation number  . Moreover,
. Moreover,
We know from Proposition 1 that each Birkhoff configuration is a configuration both with rotation number and bounded action.
We recall definitions of subsolutions and supersolutions for (1).
Definition 2[1,13-15] It is said that  and
and  are a subsolution and a supersolution of (1) respectively, if
are a subsolution and a supersolution of (1) respectively, if  for all
for all 
Lemma 2[1,13] If  is a family of subsolutions which is bounded from above (w.r.t. the partial ordering on
is a family of subsolutions which is bounded from above (w.r.t. the partial ordering on  ), then
), then  defined by
defined by
is a subsolution. Analogously, a family of supersolutions  which is bounded from below has an infimum, and
which is bounded from below has an infimum, and  is also a supersolution.
is also a supersolution.
Lemma 3[1,13] Let  be a subsolution and a supersolution, respectively, satisfying:
be a subsolution and a supersolution, respectively, satisfying:  . If
. If  or
or  is Birkhoff, then there is a Birkhoff solution
is Birkhoff, then there is a Birkhoff solution  satisfying
satisfying 
2 Main Lemmas
In this section, we propose the following theorem, which is a nontrivial generalization of Theorem 5.1 in Ref. [1].
Theorem 2 If (1) has a solution with bounded action, then (1) has a Birkhoff solution.
We should mention that Theorem A in Ref. [13] or Theorem 3.10 in Ref. [14] can also lead to Theorem 2, which relies on a gluing technique. Now we give a direct proof in this section. We would divide the process into two steps. First, we shall use the ergodic theorem to show that (1) has a solution both with bounded action and rotation number provided it has a solution with bounded action (see Lemma 4). Second, we prove further that (1) has a Birkhoff solution with rotation number  if and only if it has a solution with bounded action and rotation number
if and only if it has a solution with bounded action and rotation number  (see Lemma 7). It should be pointed out that Angenent's generalization (Theorem 5.1 in Ref. [1]) of Hall's result (Theorem 1 in Ref. [3]) can be derived by Lemma 7.
(see Lemma 7). It should be pointed out that Angenent's generalization (Theorem 5.1 in Ref. [1]) of Hall's result (Theorem 1 in Ref. [3]) can be derived by Lemma 7.
Lemma 4 If (1) has a solution with bounded action, then (1) has a solution with bounded action and rotation number.
Proof Assume that  is a solution of (1) with bounded action and
is a solution of (1) with bounded action and  as we defined in (5). We see
as we defined in (5). We see  is metrizable and
is metrizable and  is a homeomorphism on the compact metric space
is a homeomorphism on the compact metric space  . Hence, there exists a measure
. Hence, there exists a measure  , which is not only
, which is not only  -ergodic, but also
-ergodic, but also  -ergodic.
-ergodic.
We construct  , then
, then  is continuous and thus
is continuous and thus  -integrable. Applying the Birkhoff ergodic theorem[16,17], we can find
-integrable. Applying the Birkhoff ergodic theorem[16,17], we can find  such that
such that
Therefore,  is a solution of (1) with bounded action and rotation number
is a solution of (1) with bounded action and rotation number  .
.
Next, we shall construct Birkhoff solutions with certain rotation numbers.
Lemma 5 Let  . If (1) has a subsolution
. If (1) has a subsolution  and a supersolution
and a supersolution  satisfying
satisfying
then (1) has a Birkhoff solution with rotation number  .
.
Proof We define as in Lemma 2 that  and
and  Due to (6), it is evident that
Due to (6), it is evident that  and
and  are well-defined and
are well-defined and 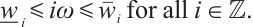 Moreover, it follows from Lemma 2 that
Moreover, it follows from Lemma 2 that  is a subsolution of (1) and
is a subsolution of (1) and  is a supersolution of (1).
is a supersolution of (1).
We shall prove that  and
and  are Birkhoff configurations. Indeed, let
are Birkhoff configurations. Indeed, let  be given and consider
be given and consider 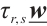 .
.
Then  , and
, and  can be proved similarly. It is easy to see that they have the same rotation number
can be proved similarly. It is easy to see that they have the same rotation number  . Applying Lemma 3, there is a Birkhoff solution with rotation number
. Applying Lemma 3, there is a Birkhoff solution with rotation number  .
.
Lemma 6 If  is a solution with bounded action and
is a solution with bounded action and
is nonempty, then for any  , there is a Birkhoff solution with rotation number
, there is a Birkhoff solution with rotation number  .
.
Proof Let  and
and 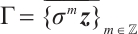 be the compact set as we defined in (5). Then
be the compact set as we defined in (5). Then  for
for  .
.
Since  yields
yields 
 we claim that there exists
we claim that there exists , such that
, such that  .
.
We argue by contradiction. Assume that for arbitrary  , there exists
, there exists  , such that
, such that  .
.
Let 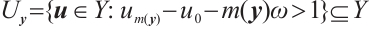 , then
, then  is an open cover of
is an open cover of  . Due to the compactness of
. Due to the compactness of  , we can find
, we can find  , such that
, such that 
For  , we have
, we have
Thus we have
Adding up the above inequalities, we obtain  Hence,
Hence,
in which  . We proceed to show that
. We proceed to show that  is unbounded.
is unbounded.
Indeed, assuming to the contrary that we can find  such that
such that 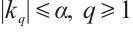 . We choose
. We choose  . Since
. Since  is a sequence consisting of integers, there is at least one
is a sequence consisting of integers, there is at least one 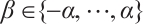 that appears infinitely in
that appears infinitely in  . Hence there exists
. Hence there exists satisfying
satisfying  But this is a contradiction to the choice of A.
But this is a contradiction to the choice of A.
Since  is unbounded, there must be a subsequence, not relabeled, such that
is unbounded, there must be a subsequence, not relabeled, such that  or
or  .
.
If  , then
, then  for
for  large enough. Hence by (7),
large enough. Hence by (7),
where  .
.
For each  large enough, there exists a large
large enough, there exists a large  such that
such that  since
since  . It is clear that
. It is clear that  . Note that
. Note that
Since  is a solution with bounded action, there exists
is a solution with bounded action, there exists  such that
such that  for all
for all 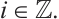 As a result, we obtain
As a result, we obtain
Then  holds automatically, which is a contradiction to the assumption that
holds automatically, which is a contradiction to the assumption that  . Similarly,
. Similarly, 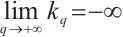 will lead to a contradiction that
will lead to a contradiction that  .
.
Hence there exists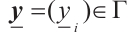 such that
such that  . Analogously, there exists
. Analogously, there exists  such that
such that  for all
for all  .
.
Let  and
and  be a lift of
be a lift of  and
and  , respectively. Since
, respectively. Since  and
and  are in
are in  ,
,  and
and  are solutions of (1). Moreover,
are solutions of (1). Moreover,
We choose 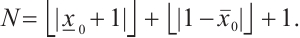 Then
Then
It follows immediately from Lemma 5 that there is a Birkhoff solution with rotation number  .
.
We are now in a position to prove Lemma 7.
Lemma 7
Equation (1) has a Birkhoff solution with rotation number  if and only if (1) has a solution with bounded action and rotation number
if and only if (1) has a solution with bounded action and rotation number  .
.
Proof Assume (1) has a Birkhoff solution with rotation number  . Then it is a solution with bounded action as we mentioned in Section 1.
. Then it is a solution with bounded action as we mentioned in Section 1.
For another direction, since  is a solution of (1) with bounded action and rotation number
is a solution of (1) with bounded action and rotation number  , we see
, we see  defined in Lemma 6 is the singleton
defined in Lemma 6 is the singleton  . We obtain by Lemma 6 that there must be a Birkhoff solution with rotation number
. We obtain by Lemma 6 that there must be a Birkhoff solution with rotation number  .
.
Combining Lemma 4 and Lemma 7 can acquire Theorem 2.
3 Proof of Theorem 1
Let  and
and  be homeomorphisms defined in Introduction. The aim of this section is to show the proof of Theorem 1.
be homeomorphisms defined in Introduction. The aim of this section is to show the proof of Theorem 1.
Proof of Theorem 1:
Since 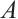 is a compact forward-invariant set for
is a compact forward-invariant set for  , one has
, one has
Then  has finite intersection property and hence
has finite intersection property and hence 
 is a nonempty compact set. On the one hand, we have
is a nonempty compact set. On the one hand, we have
On the other hand, we see by (9) that
From above, we derive that  is a compact set invariant for
is a compact set invariant for 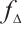 . Then for
. Then for  ,there exists
,there exists  such that
such that  is compact, where
is compact, where denotes the projection. Therefore by definition,
denotes the projection. Therefore by definition,  has an orbit
has an orbit  satisfying
satisfying
In other words,  is a solution of (1) with bounded action. Further by Theorem 2, (1) has a Birkhoff solution, implying
is a solution of (1) with bounded action. Further by Theorem 2, (1) has a Birkhoff solution, implying  has a Birkhoff orbit.
has a Birkhoff orbit.
4 Examples
We shall explain by examples the relation between variational monotone recurrence relations and monotone recurrence relations of type  .
.
On the one hand, we consider the potential function of the classical Frenkel-Kontorova model[2,18]:
Then  is a
is a  function satisfying (C1)-(C3). Let
function satisfying (C1)-(C3). Let  and
and
It turns out that  is continuous with (H1)-(H3). Hence, variational monotone recurrence relation (10) is a monotone recurrence relation of type
is continuous with (H1)-(H3). Hence, variational monotone recurrence relation (10) is a monotone recurrence relation of type  .
.
On the other hand, we consider the dissipative system:
 It is easily seen that (11) suits the definition of monotone recurrence relations of type
It is easily seen that (11) suits the definition of monotone recurrence relations of type  . We claim that (11) could not be generated by any
. We claim that (11) could not be generated by any  function
function  satisfying (C1)-(C3). In fact, if there exists
satisfying (C1)-(C3). In fact, if there exists  , such that (11) is generated by
, such that (11) is generated by  . Let
. Let
We have
where 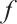 is a function of
is a function of  and
and 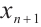 .
.
Coefficients of the cross term  of
of  and the cross term
and the cross term  of
of  are equal, that is,
are equal, that is,  We obtain by (12) that
We obtain by (12) that  which yields
which yields  , a contradiction to
, a contradiction to  .
.
References
- Angenent S B. Monotone recurrence relations, their Birkhoff orbits and topological entropy[J]. Ergodic Theory and Dynamical Systems, 1990, 10(1): 15-41. [CrossRef] [MathSciNet] [Google Scholar]
- Bangert V. Mather Sets for Twist Maps and Geodesics on Tori[M]. Wiesbaden: Vieweg+Teubner Verlag, 1988. [MathSciNet] [Google Scholar]
- Hall G R. A topological version of a theorem of Mather on twist maps[J]. Ergodic Theory and Dynamical Systems, 1984, 4(4): 585-603. [CrossRef] [MathSciNet] [Google Scholar]
- Katok A. Some remarks on Birkhoff and Mather twist map theorems[J]. Ergodic Theory and Dynamical Systems, 1982, 2(2): 185-194. [CrossRef] [MathSciNet] [Google Scholar]
- Mather J N. Existence of quasi-periodic orbits for twist homeomorphisms of the annulus[J]. Topology, 1982, 21(4): 457-467. [CrossRef] [MathSciNet] [Google Scholar]
-
Zhou T, Hu W J, Huang Q M, et al.
 -bounded orbits and Arnold tongues for quasiperiodically forced circle maps[J]. Nonlinearity, 2022, 35(3): 1119-1130.
[CrossRef]
[MathSciNet]
[Google Scholar]
-bounded orbits and Arnold tongues for quasiperiodically forced circle maps[J]. Nonlinearity, 2022, 35(3): 1119-1130.
[CrossRef]
[MathSciNet]
[Google Scholar]
- Baesens C, MacKay R S, Qin W X, et al. Depinning transition of travelling waves for particle chains[J]. Nonlinearity, 2023, 36(2): 878-901. [CrossRef] [MathSciNet] [Google Scholar]
- Guo L, Miao X Q, Wang Y N, et al. Positive topological entropy for monotone recurrence relations[J]. Ergodic Theory and Dynamical Systems, 2015, 35(6): 1880-1901. [CrossRef] [MathSciNet] [Google Scholar]
- Wang K, Miao X Q, Wang Y N, et al. Continuity of depinning force[J]. Advances in Mathematics, 2018, 335: 276-306. [CrossRef] [MathSciNet] [Google Scholar]
- Zhou T, Huang Q M. Rotation numbers and bounded deviations for quasi-periodic monotone recurrence relations[J]. Journal of Mathematical Analysis and Applications, 2024, 537(2): 128396. [CrossRef] [Google Scholar]
- Mramor B, Rink B. Ghost circles in lattice Aubry-Mather theory[J]. Journal of Differential Equations, 2012, 252(4): 3163-3208. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mramor B, Rink B W. On the destruction of minimal foliations[J]. Proceedings of the London Mathematical Society, 2014, 108(3): 704-737. [CrossRef] [MathSciNet] [Google Scholar]
- Zhou T, Qin W X. Pseudo solutions, rotation sets, and shadowing rotations for monotone recurrence relations[J]. Mathematische Zeitschrift, 2021, 297(3): 1673-1692. [CrossRef] [MathSciNet] [Google Scholar]
- Qin W X, Shen B N, Sun Y L, et al. Zero entropy and stable rotation sets for monotone recurrence relations[J]. Ergodic Theory and Dynamical Systems, 2023, 43(5):1737-1759. [CrossRef] [MathSciNet] [Google Scholar]
- Zhou T. Periodic generalized Birkhoff solutions and Farey intervals for monotone recurrence relations[J]. J Dyn Differ Equ, 2024: 10364-9. [Google Scholar]
- Katok A, Hasselblatt B. Introduction to the Modern Theory of Dynamical Systems[M]. Cambridge: Cambridge University Press, 1995. [CrossRef] [Google Scholar]
- Walters P. An Introduction to Ergodic Theory[M]. New York: Springer-Verlag, 1982. [CrossRef] [Google Scholar]
- Aubry S, Le Daeron P Y. The discrete Frenkel-Kontorova model and its extensions[J]. Physica D, 1983, 8: 381-422. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.