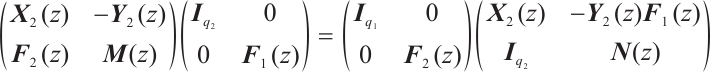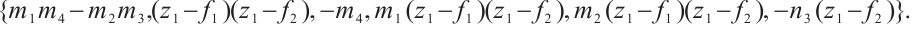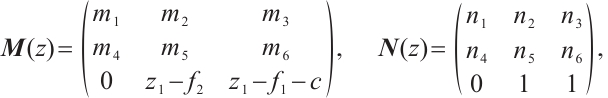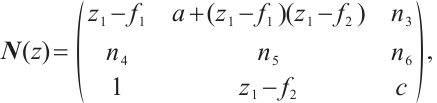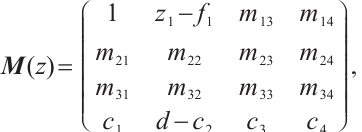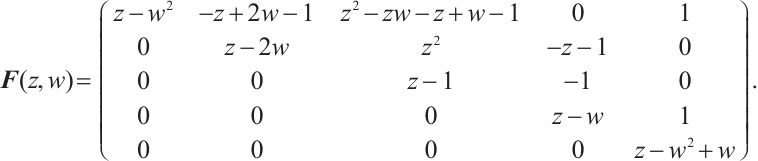| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 1, February 2025
|
|
|---|---|---|
| Page(s) | 32 - 42 | |
| DOI | https://doi.org/10.1051/wujns/2025301032 | |
| Published online | 12 March 2025 | |
Mathematics
CLC number: O151.21
On the Zero Coprime Equivalence of Multivariate Polynomial Matrices
关于多元多项式矩阵的零互素等价
1 School of Computer Science and Engineering, Hunan University of Science and Technology, Xiangtan 411201, Hunan, China
2 School of Mathematics and Statistics, Hunan University of Science and Technology, Xiangtan 411201, Hunan, China
† Corresponding author. E-mail: dmli@hnust.edu.cn
Received:
30
January
2024
The zero coprime system equivalence is one of important research in the theory of multidimensional system equivalence, and is closely related to zero coprime equivalence of multivariate polynomial matrices. We first discuss the relation between zero coprime equivalence and unimodular equivalence for polynomial matrices. Then, we investigate the zero coprime equivalence problem for several classes of polynomial matrices, some novel findings and criteria on reducing these matrices to their Smith normal forms are obtained. Finally, an example is provided to illustrate the main results.
摘要
零互素系统等价是多维系统等价理论中的重要研究内容之一,与多元多项式矩阵的零互素等价密切相关。本文首先讨论了多项式矩阵的零互素等价和幺模等价之间的关系。然后,我们研究了几类多项式矩阵的零互素等价问题,得到了将这些矩阵简化为其Smith型的一些新发现和准则。最后,通过一个例子来说明主要结果。
Key words: multidimensional system / multivariate polynomial matrix / zero coprime equivalence / unimodular equivalence / Smith normal form
关键字 : 多维系统 / 多元多项式矩阵 / 零互素等价 / 幺模等价 / Smith标准型
Cite this article: CHEN Zuo, LI Dongmei, GUO Xu. On the Zero Coprime Equivalence of Multivariate Polynomial Matrices[J]. Wuhan Univ J of Nat Sci, 2025, 30(1): 32-42.
Biography: CHEN Zuo, male, Ph. D. candidate, research direction: computer algebra. E-mail: chenzuo98@163.com
Foundation item: Supported by the National Natural Science Foundation of China (12271154), the Natural Science Foundation of Hunan Province (2022JJ30234) and the Postgraduate Scientific Research Innovation Project of Hunan Province (CX20231032)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Multidimensional ( ) systems arise naturally in signal and image processing, linear multi-channel process, iterative learning control system and integrated distributed network synthesis, etc[1-9]. The equivalence of systems is an important research topic in the field of
) systems arise naturally in signal and image processing, linear multi-channel process, iterative learning control system and integrated distributed network synthesis, etc[1-9]. The equivalence of systems is an important research topic in the field of  systems. It aims at reducing an
systems. It aims at reducing an  system to an equivalent form with fewer equations and unknowns. Since the behavioral approach to system analysis of an
system to an equivalent form with fewer equations and unknowns. Since the behavioral approach to system analysis of an  system usually resorts to the algebraic property of a multivariate polynomial matrix in the theory of
system usually resorts to the algebraic property of a multivariate polynomial matrix in the theory of  systems, the equivalence of
systems, the equivalence of  systems is closely related to the equivalence of
systems is closely related to the equivalence of  polynomial matrices. Generally, there are two kinds of the equivalence of
polynomial matrices. Generally, there are two kinds of the equivalence of  systems, unimodular system equivalence and zero coprime system equivalence. They correspond to the unimodular equivalence and zero coprime equivalence of
systems, unimodular system equivalence and zero coprime system equivalence. They correspond to the unimodular equivalence and zero coprime equivalence of  polynomial matrices, respectively.
polynomial matrices, respectively.
For single variable polynomial matrices, the two kinds of equivalence problems have been well resolved since the univariate polynomial ring has the Euclidean division property. However, when it comes to  polynomial matrices, there are still numerous unresolved issues on the two equivalence problems due to lacking mature theory of
polynomial matrices, there are still numerous unresolved issues on the two equivalence problems due to lacking mature theory of  polynomial matrices. During the past years, the unimodular equivalence for several special classes of
polynomial matrices. During the past years, the unimodular equivalence for several special classes of  polynomial matrices have been widely investigated[10-20]. For instance, Lin et al[13] proved that a matrix
polynomial matrices have been widely investigated[10-20]. For instance, Lin et al[13] proved that a matrix  with
with  is unimodular equivalent to its Smith normal form.
is unimodular equivalent to its Smith normal form.
Li et al[14-16] and Lu and Zheng et al[17-20] also presented further results on the unimodular equivalence of several classes of matrices  with
with  or
or  , where
, where  is positive integer and
is positive integer and  are irreducible polynomials, and obtained the sufficient and necessary conditions respectively for the unimodular equivalence of these matrices with their Smith normal forms. Compared with the unimodular equivalence problem, the zero coprime equivalence of
are irreducible polynomials, and obtained the sufficient and necessary conditions respectively for the unimodular equivalence of these matrices with their Smith normal forms. Compared with the unimodular equivalence problem, the zero coprime equivalence of  polynomial matrices has relatively little attention.
polynomial matrices has relatively little attention.
Zerz[21] proposed that the stability, controllability and observability of a system are closely related to its basic zero structure. Pugh[22] proved that zero coprime equivalence preserves the zero structure of the system matrix. Furthermore, Pugh et al[23] showed that a given bivariate polynomial matrix  is zero coprime equivalent to its first-level and second-level matrix pencil. In addition, Boudellioua[24] proved that
is zero coprime equivalent to its first-level and second-level matrix pencil. In addition, Boudellioua[24] proved that  polynomial matrice
polynomial matrice  is zero coprime equivalent to the greatest common divisor of the highest order minors of
is zero coprime equivalent to the greatest common divisor of the highest order minors of  under given conditions. Although the aforementioned conclusions simplify the corresponding system to a single equation form containing a single unknown, they are not easy to be executed. The Smith normal form plays an important role in the discussion of equivalence of
under given conditions. Although the aforementioned conclusions simplify the corresponding system to a single equation form containing a single unknown, they are not easy to be executed. The Smith normal form plays an important role in the discussion of equivalence of  systems because of its favorable structure and properties. The main aim of this research is to transform a given
systems because of its favorable structure and properties. The main aim of this research is to transform a given  polynomial matrix into its Smith normal form, by means of zero coprime equivalence, thereby enabling the preservation of important algebraic properties of the corresponding system.
polynomial matrix into its Smith normal form, by means of zero coprime equivalence, thereby enabling the preservation of important algebraic properties of the corresponding system.
This paper focuses on the zero coprime equivalence problem for several classes of  polynomial matrices and their Smith normal forms. Based on previous findings of zero prime factorization of
polynomial matrices and their Smith normal forms. Based on previous findings of zero prime factorization of  polynomial matrices[25,26], some new properties on the zero coprime equivalence that are
polynomial matrices[25,26], some new properties on the zero coprime equivalence that are  polynomial matrices are derived. Firstly, the relation between zero coprime equivalence and unimodular equivalence is discussed. Note that the
polynomial matrices are derived. Firstly, the relation between zero coprime equivalence and unimodular equivalence is discussed. Note that the  polynomial matrices of unimodular equivalent must be zero coprime equivalent, but the converse is not true. It is natural to associate the zero coprime equivalence problem for several classes of
polynomial matrices of unimodular equivalent must be zero coprime equivalent, but the converse is not true. It is natural to associate the zero coprime equivalence problem for several classes of  polynomial matrices which are not unimodular equivalent to their Smith normal forms. So far, the matrices such as
polynomial matrices which are not unimodular equivalent to their Smith normal forms. So far, the matrices such as  with
with  have not been shown to be equivalent to their Smith normal forms. Therefore, the following problems are also investigated.
have not been shown to be equivalent to their Smith normal forms. Therefore, the following problems are also investigated.
Problem 1: When is an  polynomial matrix
polynomial matrix  zero coprime equivalent to its Smith normal form? Here
zero coprime equivalent to its Smith normal form? Here
and  ,
,  ,
,  .
.
Problem 2: When is an  polynomial matrix
polynomial matrix  zero coprime equivalent to its Smith normal form? Here
zero coprime equivalent to its Smith normal form? Here
and  ,
,  ,
,  .
.
The rest of the paper is organized as follows. In Section 1, some basic concepts for the equivalence of polynomial matrices are introduced. In Section 2, the main results of this paper and positive answers to Problems 1 and 2 are presented. In Section 3, an example is provided to illustrate the main results and the constructive method. Section 4 concludes this paper.
1 Preliminaries
Let  is an algebraic closed field,
is an algebraic closed field,  denotes the set of polynomials in
denotes the set of polynomials in  variables
variables  with coefficients in the field
with coefficients in the field  , sometimes, we denote
, sometimes, we denote  by
by  .
.  ,
,  denotes the set of
denotes the set of  matrices with entries from
matrices with entries from  .
.  denotes the
denotes the  zero matrix and
zero matrix and  denotes the
denotes the  identity matrix. Throughout the paper, the argument
identity matrix. Throughout the paper, the argument  is omitted whenever its omission does not cause confusion.
is omitted whenever its omission does not cause confusion.
Definition 1 Let  be of normal rank
be of normal rank 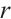 . For any
. For any  , denote
, denote  minors of
minors of 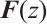 by
by  , and denote the greatest common divisor (g.c.d.) of
, and denote the greatest common divisor (g.c.d.) of  by
by  .
.
Definition 2 Let  ,
,  , the Smith normal form of
, the Smith normal form of  is defined by
is defined by  ,
,
where
 is the normal rank of
is the normal rank of  ,
,  ,
,  is the g.c.d. of the
is the g.c.d. of the  minors of
minors of  and
and  satisfies the following property
satisfies the following property
Definition 3 Let  be of full row(column) rank.
be of full row(column) rank.  is said to be zero left prime (zero right prime) if all the
is said to be zero left prime (zero right prime) if all the  (
( ) minors of
) minors of  generate unit ideal
generate unit ideal  . If
. If  is zero left prime (zero right prime), then
is zero left prime (zero right prime), then  is called simply to be ZLP (ZRP).
is called simply to be ZLP (ZRP).
Definition 4 Let  ,
,  .
.  are said to be zero left coprime if all the
are said to be zero left coprime if all the  minors of matrix
minors of matrix  generate unit ideal
generate unit ideal  . Zero right coprime can be similarly defined. If
. Zero right coprime can be similarly defined. If  are zero left coprime (zero right coprime), then
are zero left coprime (zero right coprime), then  are called simply to be ZLC (ZRC).
are called simply to be ZLC (ZRC).
Definition 5 Let  ,
,  , then
, then  are said to be unimodular equivalent if there exist
are said to be unimodular equivalent if there exist  such that
such that 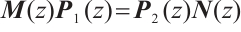 , where
, where  and
and  are unimodular matrices over
are unimodular matrices over  of appropriate dimensions.
of appropriate dimensions.
Definition 6[8] Let  , where
, where  and
and  .
.  be related by an equation of the form
be related by an equation of the form  , then
, then  and
and  are said to be zero coprime equivalent if
are said to be zero coprime equivalent if  are ZLC and
are ZLC and  are ZRC.
are ZRC.
2 Main Results
In this section, the main results are presented. First, we give some criteria for the conversion of zero coprime equivalence into unimodular equivalence through trivial expansion. Then we provide some positive answers to Problems 1 and 2.
We first introduce a useful lemma.
Lemma 1[8] The two polynomial matrices  and
and  with
with  are zero left coprime if and only if there exist
are zero left coprime if and only if there exist  and
and  polynomial matrices
polynomial matrices  and
and  such that
such that  ; The two polynomial matrices
; The two polynomial matrices  and
and  with
with  are zero right coprime if and only if there exist
are zero right coprime if and only if there exist  and
and  polynomial matrices
polynomial matrices  and
and  such that
such that  .
.
Theorem 1 Let  ,
,  be
be  polynomial matrices and
polynomial matrices and  , then
, then  ,
,  are zero coprime equivalent if and only if certain trivial expansions of them,
are zero coprime equivalent if and only if certain trivial expansions of them,  and
and  are unimodular equivalent.
are unimodular equivalent.
Proof Necessity: Suppose  are zero coprime equivalent, then there exist two matrices
are zero coprime equivalent, then there exist two matrices 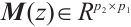 ,
,  which satisfy equation
which satisfy equation  and
and  are ZLC,
are ZLC,  are ZRC. According to Lemma 1, we have
are ZRC. According to Lemma 1, we have
where  are of appropriate dimensions.
are of appropriate dimensions.
Furthermore, we have
where  .
.
Let  , then
, then
Note that
therefore
are unimodular. Then we have following equation:
Thus,  and
and  are unimodular equivalent.
are unimodular equivalent.
Sufficiency: Let following matrices  and
and  be unimodular equivalent, then there exist two unimodular matrices
be unimodular equivalent, then there exist two unimodular matrices  ,
,  such that
such that
As can be seen from the above equation,  ,
,  .
.
Since  is a unimodular matrix, the
is a unimodular matrix, the  , this means that
, this means that  ,
,  are ZLC. By Lemma 1, then there exist two matrices
are ZLC. By Lemma 1, then there exist two matrices  such that
such that  , therefore
, therefore  are ZLC.
are ZLC.
Arguing similarly as in the above proof, we can obtain that  are ZRC. Therefore,
are ZRC. Therefore,  are zero coprime equivalent. The proof is completed.
are zero coprime equivalent. The proof is completed.
Theorem 2 Let  ,
,  be
be  polynomial matrices and
polynomial matrices and  . If
. If  and
and  are unimodular equivalent, where
are unimodular equivalent, where  , then
, then  and
and  are zero coprime equivalent.
are zero coprime equivalent.
Proof Suppose that 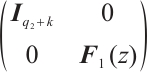 and
and  are unimodular equivalent, then we can obtain that they are zero coprime equivalent. We construct the following equation
are unimodular equivalent, then we can obtain that they are zero coprime equivalent. We construct the following equation
where  and
and  .
.
Obviously,  and
and  are zero coprime equivalent. According to the transitivity of zero coprime equivalence, we can further obtain that
are zero coprime equivalent. According to the transitivity of zero coprime equivalence, we can further obtain that  and
and  are zero coprime equivalent. The proof is completed.
are zero coprime equivalent. The proof is completed.
Based on Theorems 1 and 2, we establish the relationship between zero coprime equivalence and unimodular equivalence of  polynomial matrices. Next, we propose some important results for the zero coprime equivalence of several classes of
polynomial matrices. Next, we propose some important results for the zero coprime equivalence of several classes of  polynomial matrices and their Smith normal forms.
polynomial matrices and their Smith normal forms.
Theorem 3 Let  have the following form
have the following form
where  ,
,  and
and  . If all the
. If all the  minors of
minors of  have a common zero and factor coprime, then
have a common zero and factor coprime, then  is not zero coprime equivalent to its Smith normal form
is not zero coprime equivalent to its Smith normal form  , where
, where  .
.
Proof Suppose that there exist  satisfies
satisfies  , where
, where
We have
then
From the equations (2) and (3), we can solve to obtain that  and
and  . Then we consider all the
. Then we consider all the  minors of
minors of  ,
,
Suppose that all the  minors of
minors of  have a common zero
have a common zero  . It is seen that
. It is seen that  . So the
. So the  minors of
minors of  have a common zero
have a common zero  . Therefore,
. Therefore,  is not zero coprime equivalent to its Smith normal form. The proof is completed.
is not zero coprime equivalent to its Smith normal form. The proof is completed.
Remark 1 By Definition 5 and Definition 6, we have that if two  polynomial matrices are unimodular equivalent, then they must be zero coprime equivalent. Meanwhile, two polynomial matrices that are not zero coprime equivalent imply that they are not unimodular equivalent. Therefore, Theorem 3 can be used to determine whether two matrices are not unimodular equivalent. Furthermore, Proposition 2.9 of Liu et al[10] is a special case of Theorem 3.
polynomial matrices are unimodular equivalent, then they must be zero coprime equivalent. Meanwhile, two polynomial matrices that are not zero coprime equivalent imply that they are not unimodular equivalent. Therefore, Theorem 3 can be used to determine whether two matrices are not unimodular equivalent. Furthermore, Proposition 2.9 of Liu et al[10] is a special case of Theorem 3.
In addition, we consider  polynomial matrices
polynomial matrices  with the
with the  minors generating unit ideal
minors generating unit ideal  . In general this kind of matrix
. In general this kind of matrix  may not be unimodular equivalent to their Smith normal forms, see examples in Frost and Storey[27] or the following matrix,
may not be unimodular equivalent to their Smith normal forms, see examples in Frost and Storey[27] or the following matrix,
by Proposition 2.10 in Ref.[10],  is not unimodular equivalent to its Smith normal form.
is not unimodular equivalent to its Smith normal form.
Specially, Li et al[14] showed that even for the case that
where  are different and the
are different and the 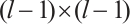 minors of
minors of  generate
generate  ,
,  may not be unimodular equivalent to its Smith normal form. In what follows, we investigate the conditions under which such matrices are zero coprime equivalent to their Smith normal forms.
may not be unimodular equivalent to its Smith normal form. In what follows, we investigate the conditions under which such matrices are zero coprime equivalent to their Smith normal forms.
Let  and
and
where  ,
,  . According to Definition 2, the Smith normal form of
. According to Definition 2, the Smith normal form of  is
is
Theorem 4 Let  with form in (4) and
with form in (4) and  . If
. If  have no common zeros in the field
have no common zeros in the field  , then
, then  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  .
.
Proof Let
where  ,
,  , such that
, such that  , i.e.
, i.e.
obviously,  ,
,  .
.
Then  , and we have
, and we have  . Then
. Then  , from the equation above, we have
, from the equation above, we have 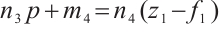 , or equivalently
, or equivalently  .
.
Now, we consider all the  minors of matrix
minors of matrix  :
:
Let  , then
, then  . Since
. Since 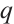 and
and  have no common zeros in the field
have no common zeros in the field  ,
, 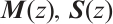 are ZLC.
are ZLC.
We next prove that  are ZRC. Since
are ZRC. Since  , by computing, the
, by computing, the  minors of matrix
minors of matrix  give
give
Because  and
and 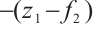 have no common zeros,
have no common zeros,  are ZRC. Therefore,
are ZRC. Therefore,  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  . The proof is completed.
. The proof is completed.
It follows from Theorem 4 that Problem 1 is correct for the case of  . And then, we extend the conclusions and focus on the case of
. And then, we extend the conclusions and focus on the case of  .
.
Theorem 5 Let  have the following form
have the following form
where  and
and  . Let
. Let  . If
. If  have no common zeros in the field
have no common zeros in the field  , then
, then  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  , where
, where
Proof Let
satisfy equation  , where
, where  .
.
Now, we consider the  minors of matrix
minors of matrix  , where
, where
there exist two  minors as follows
minors as follows
Note that  and
and  have no common zeros in the field
have no common zeros in the field  , therefore
, therefore  are ZLC.
are ZLC.
Next, we consider the  minors of matrix
minors of matrix  , where
, where
similarly, there exist two  minors as follows
minors as follows
So the  minors of matrix
minors of matrix  have no common zeros in the field
have no common zeros in the field  , therefore
, therefore  are ZRC. With the help of the above conclusions,
are ZRC. With the help of the above conclusions,  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  . The proof is completed.
. The proof is completed.
Theorem 6 Let  have the following form:
have the following form:
where  ,
,  and
and  . Let
. Let  . If
. If  have no common zeros in the field
have no common zeros in the field  , then
, then  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  , where
, where
Proof Let
where  ,
,  and satisfy equation
and satisfy equation  .
.
Arguing similarly as in the proof of Theorem 5, it is easy to prove that  are ZLC and
are ZLC and  are ZRC. Therefore,
are ZRC. Therefore,  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  . The proof is completed.
. The proof is completed.
Theorem 6 gives a positive answer to Problem 1. Next, we will investigate Problem 2 and develop some new results concerning Theorem 4.
Theorem 7 Let  with form in (4). If
with form in (4). If  and
and  have no common zeros in the field
have no common zeros in the field 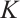 , then
, then 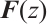 is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  .
.
Proof Assume
where 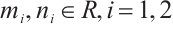 and satisfies equation
and satisfies equation  ,
,
Arguing similarly as in the proof of Theorem 4, it is also easy to prove that  are ZLC and
are ZLC and  are ZRC. Therefore,
are ZRC. Therefore,  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  . The proof is completed.
. The proof is completed.
Theorem 8 Let  have the following form
have the following form  where
where  and
and  . If the last two columns of
. If the last two columns of  construct a ZRP matrix, then
construct a ZRP matrix, then  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  , where
, where 
Proof Let
where  and satisfy equation
and satisfy equation  .
.
Setting  from the assumption,
from the assumption,  is a ZRP matrix such that all the
is a ZRP matrix such that all the  minors
minors  generate unit ideal
generate unit ideal  .
.
Now, we consider the  minors of matrix
minors of matrix  . By computation, there exist three minors in all the
. By computation, there exist three minors in all the  minors as follows
minors as follows
It is clear that the  minors of matrix
minors of matrix  generate
generate  , therefore
, therefore  are ZLC.
are ZLC.
Next, we consider the  minors of matrix
minors of matrix  . Similarly, there exist three minors in all the
. Similarly, there exist three minors in all the  minors as follows
minors as follows
So the  minors of matrix
minors of matrix  generate
generate  , therefore
, therefore  are ZRC. As mentioned earlier,
are ZRC. As mentioned earlier,  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  . The proof is completed.
. The proof is completed.
In what follows, we will focus on the case of  , where
, where  , as presented in the following theorem.
, as presented in the following theorem.
Theorem 9 Let  have the following form
have the following form
where  If the last
If the last  columns of
columns of  construct a ZRP matrix, then
construct a ZRP matrix, then  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  , where
, where
Proof We first prove the case of  . Let
. Let
by computing,  , the
, the  minors of matrix
minors of matrix  as follows:
as follows:
From the assumption that matrix  is ZRP, we have that
is ZRP, we have that  generate unit ideal
generate unit ideal  .
.
Let
satisfy the equation  , where
, where 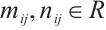 .
.
Next we consider the  minors of matrix
minors of matrix  . Since the polynomials
. Since the polynomials  belong to the
belong to the  minors of matrix
minors of matrix  ,
,  are ZLC. Similarly, we obtain that
are ZLC. Similarly, we obtain that 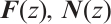 are ZRC. Therefore,
are ZRC. Therefore,  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  .
.
Using a process similar to the above proof, we can straightforwardly get the result for the case of  . Therefore,
. Therefore, 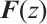 is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  for
for  . The proof is completed.
. The proof is completed.
Remark 2 Combining Theorem 7, Theorem 8 and Theorem 9, we give a positive answer to Problem 2.
3 Example
In this section, we give an example to illustrate the main results.
Example 1 Consider a 2D polynomial matrix of 
By computing, let  and the last 4 columns of
and the last 4 columns of  construct a ZRP matrix. Obviously, the Smith normal forms of
construct a ZRP matrix. Obviously, the Smith normal forms of  is following matrix
is following matrix
Let
calculating all the  minors of matrix
minors of matrix  as follows:
as follows:
Setting
where 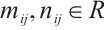 , such that satisfy equation
, such that satisfy equation  , we consider that the
, we consider that the  minors of matrix
minors of matrix  have a fifth order minor which is equal to 1, therefore,
have a fifth order minor which is equal to 1, therefore,  are ZLC. Similarly, by calculating the
are ZLC. Similarly, by calculating the  minors of matrix
minors of matrix  , we find that there is also a fifth order minor which is equal to 1, then
, we find that there is also a fifth order minor which is equal to 1, then  are ZRC. Thus,
are ZRC. Thus,  is zero coprime equivalent to its Smith normal form
is zero coprime equivalent to its Smith normal form  .
.
4 Conclusion
In this paper, we first propose some criteria for the conversion of zero coprime equivalence into unimodular equivalence through trivial expansion. Then we investigate the zero coprime equivalence problem of several kinds of  polynomial matrices over an algebraic closed field. In general, it is observed that certain multivariate polynomial triangular matrices are not zero coprime equivalent to their Smith normal forms (Theorem 3). Afterwards, we are devoted to studying the zero coprime equivalence and reduction of several classes of multivariate polynomial matrices that are not unimodular equivalent to their Smith normal forms. We present two problems in this aspect and given positive answers to them. An illustrative example has also been comprehensively analyzed towards the end.
polynomial matrices over an algebraic closed field. In general, it is observed that certain multivariate polynomial triangular matrices are not zero coprime equivalent to their Smith normal forms (Theorem 3). Afterwards, we are devoted to studying the zero coprime equivalence and reduction of several classes of multivariate polynomial matrices that are not unimodular equivalent to their Smith normal forms. We present two problems in this aspect and given positive answers to them. An illustrative example has also been comprehensively analyzed towards the end.
References
- Bose N K. Applied Multidimensional Systems Theory[M]. New York: Van Nostrand Reinhold, 1982. [Google Scholar]
- Dudgeon D E, Mersereau R M. Multidimensional Digital Signal Processing[M]. Englewood Cliffs: Prentice Hall, 1984. [Google Scholar]
- Bose N K. Digital Filters: Theory and Applications[M]. Amsterdam: Elsevier Science, 1985. [Google Scholar]
- Bose N K, Liang P. Neural Network Fundamentals with Graphs, Algorithms and Applications[M]. New York: McGraw-Hill, 1996. [Google Scholar]
- Bose N K, Buchberger B, Guiver J. Multidimensional Systems Theory and Applications[M]. Dordrecht: Kluwer, 2003. [Google Scholar]
- Roesser R. A discrete state-space model for linear image processing[J]. IEEE Transactions on Automatic Control, 1975, 20(1): 1-10. [Google Scholar]
- Fornasini E, Marchesini G. State-space realization theory of two-dimensional filters[J]. IEEE Transactions on Automatic Control, 1976, 21(4): 484-492. [CrossRef] [MathSciNet] [Google Scholar]
- Youla D, Gnavi G. Notes on n-dimensional system theory[J]. IEEE Transactions on Circuits and Systems, 1979, 26(2): 105-111. [CrossRef] [MathSciNet] [Google Scholar]
- McInerney S J. Representations and Transformations for Multi-Dimensional Systems[D]. Loughborough: Loughborough University, 1999. [Google Scholar]
- Liu J W, Wu T, Li D M. Smith form of triangular multivariate polynomial matrix[J]. Journal of Systems Science and Complexity, 2023, 36(1): 151-164. [CrossRef] [MathSciNet] [Google Scholar]
- Boudellioua M S. Further results on the equivalence to Smith form of multivariate polynomial matrices[J]. Control and Cybernetics, 2013, 42(2): 543-551. [MathSciNet] [Google Scholar]
- Frost M G, Boudellioua M S. Some further results concerning matrices with elements in a polynomial ring[J]. International Journal of Control, 1986, 43(5): 1543-1555. [CrossRef] [MathSciNet] [Google Scholar]
- Lin Z P, Boudellioua M S, Xu L. On the equivalence and factorization of multivariate polynomial matrices[C]//2006 IEEE International Symposium on Circuits and Systems (ISCAS). New York: IEEE, 2006: 4911-4914. [Google Scholar]
- Li D M, Liu J W, Chu D L. The Smith form of a multivariate polynomial matrix over an arbitrary coefficient field[J]. Linear and Multilinear Algebra, 2022, 70(2): 366-379. [CrossRef] [MathSciNet] [Google Scholar]
- Li D M, Liu J W, Zheng L C. On the equivalence of multivariate polynomial matrices[J]. Multidimensional Systems and Signal Processing, 2017, 28(1): 225-235. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Li D, Liang R, Liu J. Some further results on the Smith form of bivariate polynomial matrices[J]. Journal of System Science and Mathematical Science, 2019, 39(12): 1983-1997. [Google Scholar]
- Lu D, Wang D K, Xiao F H. New remarks on the factorization and equivalence problems for a class of multivariate polynomial matrices[J]. Journal of Symbolic Computation, 2023, 115: 266-284. [CrossRef] [MathSciNet] [Google Scholar]
- Zheng X P, Lu D, Wang D K, et al. New results on the equivalence of bivariate polynomial matrices[J]. Journal of Systems Science and Complexity, 2023, 36(1): 77-95. [CrossRef] [MathSciNet] [Google Scholar]
- Lu D, Wang D K, Xiao F H, et al. Equivalence and reduction of bivariate polynomial matrices to their Smith forms[J]. Journal of Symbolic Computation, 2023, 118: 1-16. [CrossRef] [MathSciNet] [Google Scholar]
- Lu D, Wang D K, Xiao F H. Further results on the factorization and equivalence for multivariate polynomial matrices[C]//Proceedings of the 45th International Symposium on Symbolic and Algebraic Computation. New York: ACM, 2020: 328-335. [Google Scholar]
- Zerz E. Primeness of multivariate polynomial matrices[J]. Systems & Control Letters, 1996, 29(3): 139-145. [CrossRef] [MathSciNet] [Google Scholar]
- Pugh A C. Matrix pencil equivalents of a general 2-D polynomial matrix[J]. International Journal of Control, 1998, 71(6): 1027-1050. [CrossRef] [MathSciNet] [Google Scholar]
- Pugh A C, McInerney S J, El-Nabrawy E M O. Zero structures of n-D systems[J]. International Journal of Control, 2005, 78(4): 277-285. [CrossRef] [MathSciNet] [Google Scholar]
- Boudellioua M S. Reduction of linear functional systems using Fuhrmann's equivalence[J]. Sultan Qaboos University Journal for Science, 2016, 21(1): 64-68 [CrossRef] [Google Scholar]
- Wang M S, Feng D G. On Lin-Bose problem[J]. Linear Algebra and Its Applications, 2004, 390: 279-285. [CrossRef] [MathSciNet] [Google Scholar]
- Mingsheng W, Kwong C P. On multivariate polynomial matrix factorization problems[J]. Mathematics of Control, Signals and Systems, 2005, 17(4): 297-311. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Frost M G, Storey C. Equivalence of matrices over R[s, z]: A counter-example[J]. International Journal of Control, 1981, 34(6): 1225-1226. [CrossRef] [MathSciNet] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.