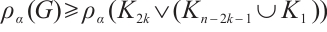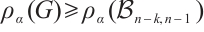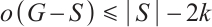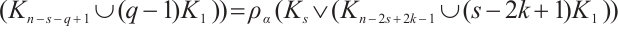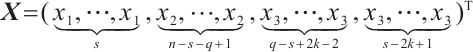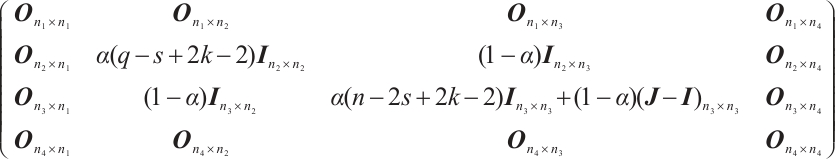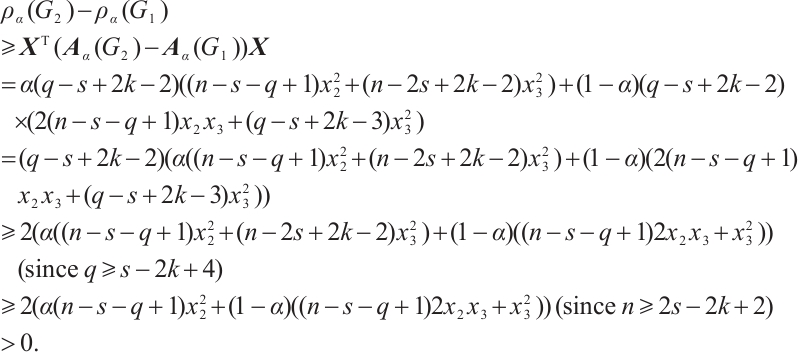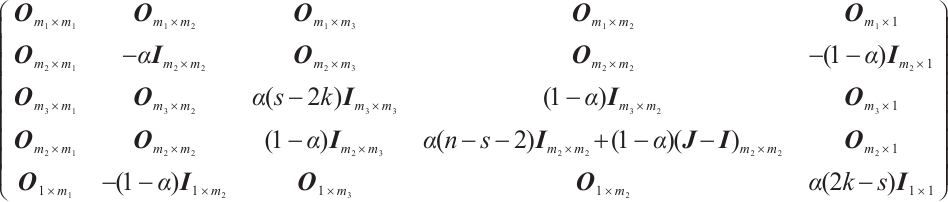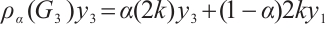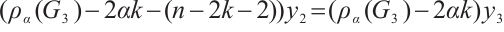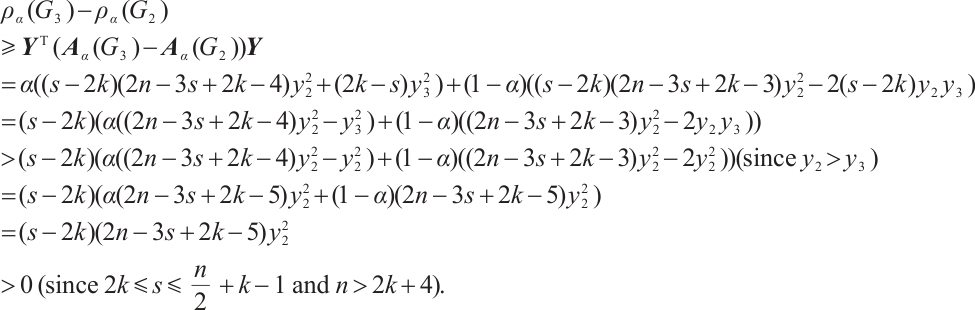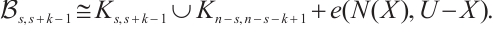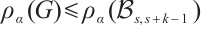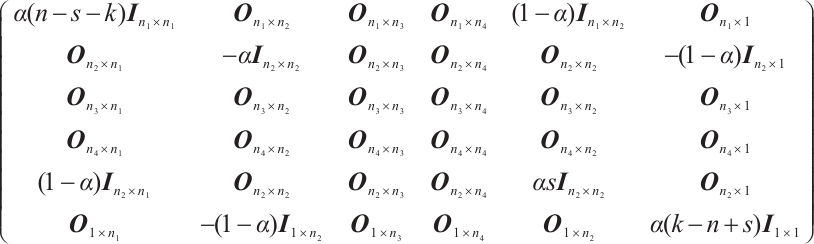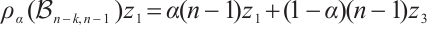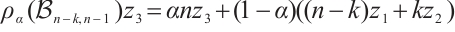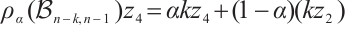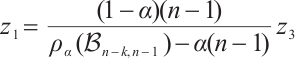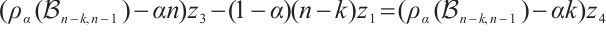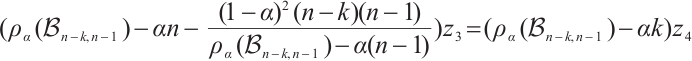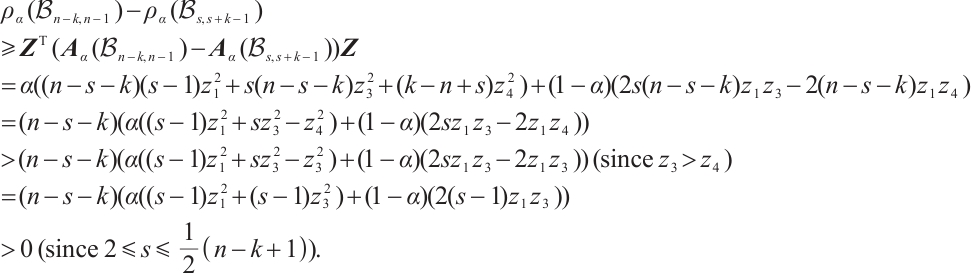| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 2, April 2025
|
|
|---|---|---|
| Page(s) | 118 - 124 | |
| DOI | https://doi.org/10.1051/wujns/2025302118 | |
| Published online | 16 May 2025 | |
Mathematics
CLC number: O157.5
The Aα-Spectral Radius and k-Extendability in Graphs
图的Aα-谱半径与k-可扩展性
Institute of Applied Mathematics, Lanzhou Jiaotong University, Lanzhou 730070, Gansu, China
† Corresponding author. E-mail: wenfei@lzjtu.edu.cn
Received:
19
May
2024
A graph is called 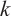 -extendable if each
-extendable if each 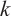 -matching can be extended to a perfect matching. In this paper, we provide a sufficient condition in terms of the
-matching can be extended to a perfect matching. In this paper, we provide a sufficient condition in terms of the 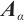 -spectral radius for the
-spectral radius for the 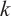 -extendability of a connected graph and characterize the corresponding extremal graphs. In addition, such an
-extendability of a connected graph and characterize the corresponding extremal graphs. In addition, such an 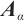 -spectral condition of a connected balanced bipartite graph is also considered, and the corresponding extremal graphs are determined.
-spectral condition of a connected balanced bipartite graph is also considered, and the corresponding extremal graphs are determined.
摘要
若一个图的任意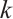 -匹配都可扩展为该图的完美匹配,则称此图为
-匹配都可扩展为该图的完美匹配,则称此图为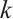 -可扩展图。本文给出了连通图具有
-可扩展图。本文给出了连通图具有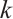 -可扩展性的一个
-可扩展性的一个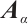 -谱条件,并刻画了相应的极图。此外,还考虑了连通平衡二部图具有
-谱条件,并刻画了相应的极图。此外,还考虑了连通平衡二部图具有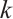 -可扩展性的一个
-可扩展性的一个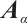 -谱条件及其相应的极图。
-谱条件及其相应的极图。
Key words: Aα-spectral radius / matching / k-extendable graph
关键字 : Aα-谱半径 / 匹配 / k-可扩展图
Cite this article: HA Jing, WEN Fei. The Aα-Spectral Radius and k-Extendability in Graphs[J]. Wuhan Univ J of Nat Sci, 2025, 30(2): 118-124.
Biography: HA Jing, female, Master candidate, research direction: graph theory. E-mail: hajing0224@163.com
Foundation item: Supported by the National Natural Science Foundation of China (11961041, 12261055) and the Key Project of Natural Science Foundation of Gansu Province (24JRRA222)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
All graphs considered are undirected, simple, and connected throughout this paper. Let 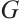 be a graph with vertex set
be a graph with vertex set  and edge set
and edge set 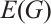 . We denote by
. We denote by 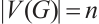 and
and 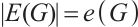 the order and the size of
the order and the size of 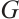 , respectively. Moreover, we write
, respectively. Moreover, we write 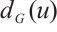 for the degree of vertex
for the degree of vertex 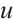 in
in 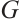 , and
, and 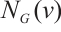 for the neighbor set of vertex
for the neighbor set of vertex 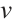 in
in 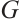 . For any
. For any 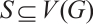 , let
, let 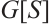 be the subgraph of
be the subgraph of 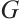 induced by
induced by 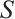 , and let
, and let 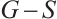 be the subgraph induced by
be the subgraph induced by 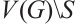 . The set of all edges between two vertex sets
. The set of all edges between two vertex sets 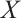 and
and 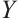 is denoted by
is denoted by 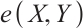 . For any two graphs
. For any two graphs 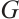 and
and 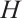 , we denote by
, we denote by  the disjoint union of
the disjoint union of 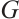 and
and 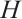 . The join
. The join  is the graph obtained from
is the graph obtained from  by adding all possible edges between
by adding all possible edges between  and
and 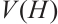 .
.
The adjacency matrix 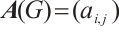 of
of  is a
is a  symmetric matrix, whose entries
symmetric matrix, whose entries 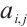 are given by
are given by 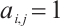 if
if 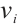 and
and  are adjacent in
are adjacent in 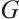 , and
, and 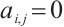 otherwise. The degree diagonal matrix of
otherwise. The degree diagonal matrix of 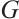 is denoted by
is denoted by 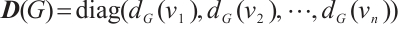 , where
, where 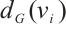 is the degree of
is the degree of 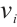 in
in  . For any real
. For any real  , Nikiforov[1] defined the
, Nikiforov[1] defined the 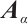 -matrix of
-matrix of  as
as 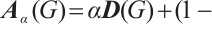
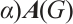 . The largest eigenvalue of
. The largest eigenvalue of 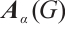 is called the
is called the 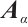 -spectral radius of
-spectral radius of 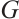 , and denoted by
, and denoted by 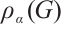 . Obviously,
. Obviously, 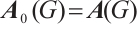 ,
, 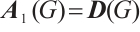 and
and 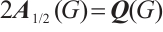
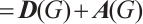 , where
, where 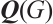 is the signless Laplacian matrix of
is the signless Laplacian matrix of 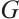 . Note that
. Note that 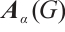 is a real symmetric non-negative matrix. By the Perron-Frobenius Theorem,
is a real symmetric non-negative matrix. By the Perron-Frobenius Theorem, 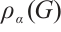 is a positive number and there exists a unique positive unit eigenvector corresponding to
is a positive number and there exists a unique positive unit eigenvector corresponding to 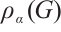 , which is called the Perron vector of
, which is called the Perron vector of 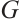 .
.
A graph is 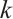 -extendable if each matching consisting of
-extendable if each matching consisting of 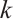 edges can be extended to a perfect matching. Clearly, the existence of a perfect matching can be regarded as 0-extendability. The concept of
edges can be extended to a perfect matching. Clearly, the existence of a perfect matching can be regarded as 0-extendability. The concept of 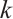 -extendability gradually evolved from the concept of elementary (that is, 1-extendable) bipartite graphs. In 1980, Plummer[2] gave the first results on
-extendability gradually evolved from the concept of elementary (that is, 1-extendable) bipartite graphs. In 1980, Plummer[2] gave the first results on 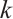 -extendable graphs for arbitrary
-extendable graphs for arbitrary 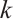 , he studied the properties of
, he studied the properties of 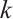 -extendable graphs and proved that nearly all
-extendable graphs and proved that nearly all 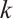 -extendable graphs
-extendable graphs 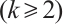 are
are 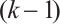 -extendable and
-extendable and 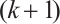 -connected. Then Plummer[3-4] provided the relationships between the toughness and genus of a graph and the
-connected. Then Plummer[3-4] provided the relationships between the toughness and genus of a graph and the 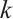 -extendability of the graph. Moreover, many researchers further studied the relationship between
-extendability of the graph. Moreover, many researchers further studied the relationship between 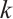 -extendability and other graph parameters, such as minimum degree, connectivity, binding number, and independence number etc[5-10].
-extendability and other graph parameters, such as minimum degree, connectivity, binding number, and independence number etc[5-10].
In the past few years, much attention has been paid to the connections of the spectral radius and the 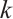 -extendable graphs. Fan and Lin[11] investigated the adjacency spectral conditions for a graph (as well as a balanced bipartite graph) with a minimum degree
-extendable graphs. Fan and Lin[11] investigated the adjacency spectral conditions for a graph (as well as a balanced bipartite graph) with a minimum degree 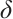 to be
to be 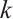 -extendable. In Ref. [12], Zhou and Zhang gave a lower bound on the signless Laplacian spectral radius to ensure that
-extendable. In Ref. [12], Zhou and Zhang gave a lower bound on the signless Laplacian spectral radius to ensure that 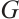 is
is 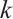 -extendable. Then, Zhang and Dam[13] studied the
-extendable. Then, Zhang and Dam[13] studied the 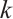 -extendability of graphs from a distance spectral perspective. The main goal of this paper is to study the relationship between
-extendability of graphs from a distance spectral perspective. The main goal of this paper is to study the relationship between 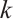 -extendability of graphs and the
-extendability of graphs and the 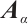 -spectral radius.
-spectral radius.
In the following, we first provide a condition for the 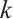 -extendability of matchings in a graph in terms of the
-extendability of matchings in a graph in terms of the 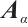 -spectral radius.
-spectral radius.
Theorem 1 Let 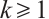 be an integer, and let
be an integer, and let 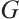 be a connected graph of even order
be a connected graph of even order 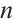 with
with 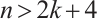 . For
. For  , if
, if
then 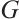 is
is 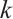 -extendable, unless
-extendable, unless 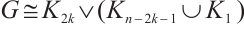 .
.
A bipartite graph is called balanced if both parts of the bipartition have equal size. Note that every bipartite graph with a perfect matching must be balanced. Hence a 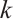 -extendable bipartite graph must be balanced. Furthermore, we denote by
-extendable bipartite graph must be balanced. Furthermore, we denote by 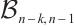 the bipartite graph obtained from
the bipartite graph obtained from  by attaching a vertex to
by attaching a vertex to 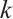 vertices in
vertices in 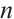 -vertex part (see Fig. 1). In Ref. [13], Zhang and Dam gave a sufficient condition in terms of the distance spectral radius for the
-vertex part (see Fig. 1). In Ref. [13], Zhang and Dam gave a sufficient condition in terms of the distance spectral radius for the 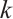 -extendability of a bipartite graph. Along this line, we have the result below.
-extendability of a bipartite graph. Along this line, we have the result below.
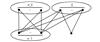 |
Fig. 1 The extremal graph 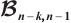
|
Theorem 2 Let 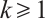 be an integer, and let
be an integer, and let  be a connected balanced bipartite graph of order
be a connected balanced bipartite graph of order 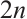 with
with  . For
. For  , if
, if
then 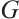 is
is 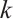 -extendable, unless
-extendable, unless 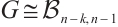 , see Fig. 1 for instance.
, see Fig. 1 for instance.
1 Preliminaries
In this section, we give several preliminary lemmas, which are useful to the proof of our main results.
For any 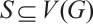 , let
, let 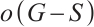 denote the number of odd components in
denote the number of odd components in 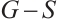 . In 1995, Chen[7] provided a necessary and sufficient condition for the existence of
. In 1995, Chen[7] provided a necessary and sufficient condition for the existence of 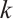 -extendable graphs.
-extendable graphs.
Lemma 1[7] Let 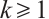 . A graph
. A graph 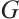 is
is 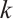 -extendable if and only if
-extendable if and only if
for any 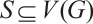 such that
such that 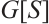 contains
contains 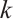 independent edges.
independent edges.
Lemma 2[1] If 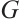 is connected, and
is connected, and 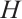 is a proper subgraph of
is a proper subgraph of 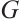 , then
, then 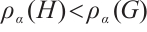 for any
for any  .
.
Given any 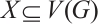 , let
, let 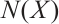 be the set of all neighbors of the vertices in
be the set of all neighbors of the vertices in 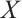 . In Ref. [14], Plummer gave the necessary and sufficient conditions for bipartite graphs to be
. In Ref. [14], Plummer gave the necessary and sufficient conditions for bipartite graphs to be 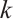 -extendable.
-extendable.
Lemma 3[14] Let  and let
and let 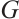 be a connected bipartite graph with parts
be a connected bipartite graph with parts 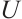 and
and 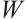 . Then the following are equivalent:
. Then the following are equivalent:
(i) 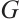 is
is 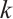 -extendable;
-extendable;
(ii) 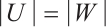 and for all nonempty subsets
and for all nonempty subsets 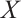 of
of 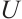 , if
, if 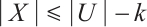 , then
, then 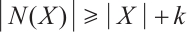 ;
;
(iii) For all 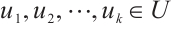 and
and 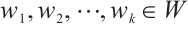 , the graph
, the graph 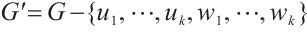 has a perfect matching.
has a perfect matching.
Finally, we need a known result mentioned as Claim 1 of the proof of Theorem 1.1 in Ref. [15].
Lemma 4[15] Let  be positive integers and
be positive integers and 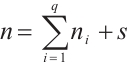 . For
. For  ,we have
,we have 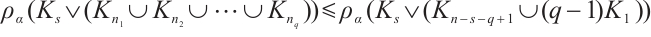 , where the equality holds if and only if
, where the equality holds if and only if 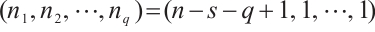 .
.
2 Proof of Theorem 1
In this section, we elaborate on the proof of Theorem 1, which provides a sufficient condition via the 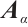 -spectral radius of a connected graph to ensure that the graph is
-spectral radius of a connected graph to ensure that the graph is 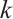 -extendable.
-extendable.
Proof of Theorem 1 Suppose to the contrary that 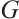 is not
is not 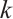 -extendable, we will prove that if
-extendable, we will prove that if 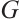 is not
is not  -extendable, then
-extendable, then 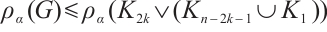 with equality only if
with equality only if 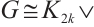
 . By Lemma 1, there exists some nonempty subset
. By Lemma 1, there exists some nonempty subset 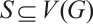 , such that
, such that  and
and 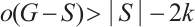 . For convenience, let
. For convenience, let 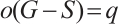 and
and 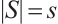 . We assert that
. We assert that 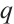 and
and 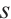 have the same parity. If
have the same parity. If 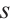 is odd, then
is odd, then  is an odd number since
is an odd number since 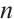 is even, and so, the number of odd components in
is even, and so, the number of odd components in 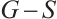 is odd, i.e.,
is odd, i.e.,  is odd. Hence,
is odd. Hence, 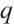 and
and 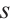 are odd. Similarly, we obtain that
are odd. Similarly, we obtain that  is even if
is even if 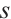 is even. Thus, it concludes that
is even. Thus, it concludes that 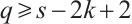 . To promote the proof, we have the following three claims.
. To promote the proof, we have the following three claims.
Claim 1 For some odd integers  and
and 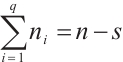 ,
, 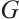 is a spanning subgraph of
is a spanning subgraph of 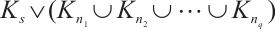 .
.
Proof Let 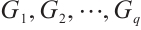 be the orders of the
be the orders of the 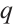 odd components of
odd components of 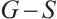 with
with 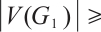
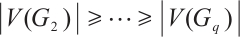 , and let
, and let 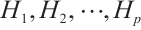 be the
be the 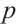 even components of
even components of  . Without loss of generality, we assume that all even components join to component
. Without loss of generality, we assume that all even components join to component 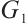 , i.e.,
, i.e.,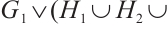
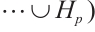 . So,
. So, 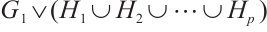 is the spanning subgraph of
is the spanning subgraph of 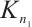 for some integer
for some integer 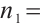
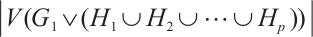 , and
, and 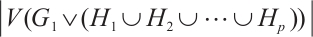 is an odd integer. Let
is an odd integer. Let 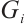 be the spanning subgraph of
be the spanning subgraph of 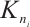 for some
for some 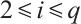 and
and 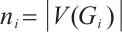 . Then all components of
. Then all components of  are odd and
are odd and 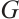 is the spanning subgraph of
is the spanning subgraph of  , and thus,
, and thus, 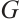 is a spanning subgraph of
is a spanning subgraph of 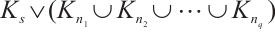 for some odd integers
for some odd integers  and
and 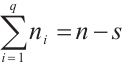 .
.
Furthermore, by Lemma 2 we have  with equality holds if and only if
with equality holds if and only if  .
.
If  , then
, then  , say
, say  .
.
Hence, by Lemma 4 we have that 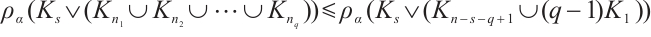 , where the equality holds if and only if
, where the equality holds if and only if 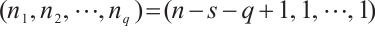 .
.
Note that 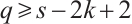 . Let
. Let 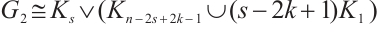 . We next compare the
. We next compare the 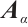 -spectral radius of
-spectral radius of 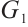 and
and 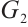 in the following.
in the following.
Claim 2 For  , we have
, we have 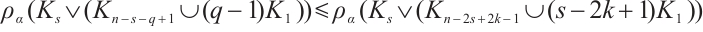 with equality holds if and only if
with equality holds if and only if 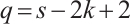 .
.
Proof If 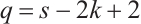 , we have
, we have 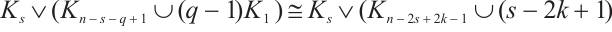
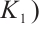 . Hence,
. Hence, 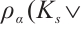
Now we consider 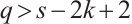 . Clearly,
. Clearly, 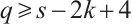 since
since 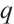 and
and 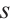 has the same parity, here it is sufficient to prove
has the same parity, here it is sufficient to prove 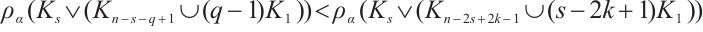 for
for 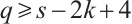 . We notice that
. We notice that 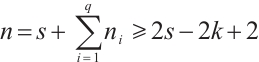 ,
, 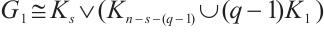 and
and 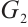
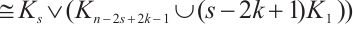 .
.
Suppose that 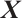 is the unit Perron eigenvector of
is the unit Perron eigenvector of 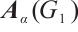 , and
, and 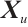 denotes the entry of
denotes the entry of 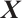 corresponding to the vertex
corresponding to the vertex 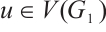 . From the equitable partition
. From the equitable partition 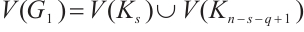
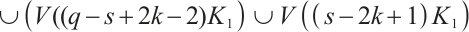 , we have that
, we have that 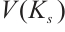 ,
,  and
and 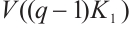 has the same entries in
has the same entries in 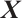 . Let
. Let 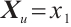 for
for 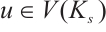 ,
, 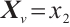 for
for 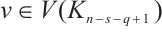 and
and 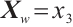 for
for 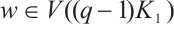 , respectively. For convenience, we write
, respectively. For convenience, we write 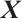 as follows:
as follows:
For the graph 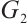 , we partition
, we partition 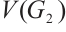 as
as 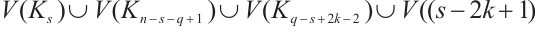
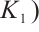 . Thus,
. Thus, 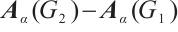 has the form of a block matrix below:
has the form of a block matrix below:
where 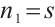 ,
,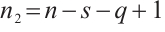 ,
,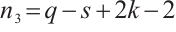 and
and 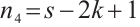 , meanwhile,
, meanwhile, 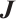 is an all-ones matrix and
is an all-ones matrix and  is an identity matrix.
is an identity matrix.
Furthermore, by Rayleigh's principle, we have
Therefore, 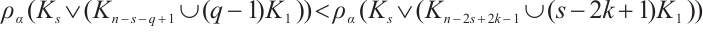 .
.
Recall that 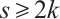 . Let
. Let 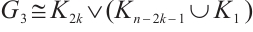 . Next, we compare the
. Next, we compare the 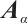 -spectral radius of
-spectral radius of 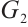 and
and 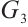 and give the following claim.
and give the following claim.
Claim 3 Let 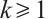 and
and 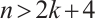 . For
. For  , we have
, we have 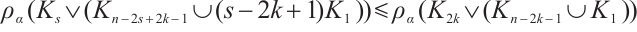
with equality holds if and only if 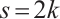 .
.
Proof If 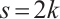 , we have
, we have 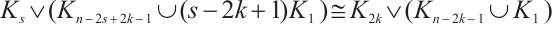 . Hence,
. Hence, 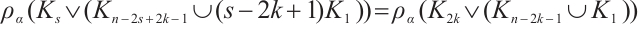 .
.
If 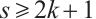 , we should verify that
, we should verify that 
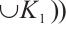 . Since
. Since  we have
we have 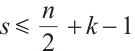 . Thus, it concludes that
. Thus, it concludes that 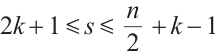 . Note that
. Note that  and
and 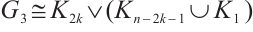 .
.
Let 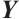 be the unit Perron eigenvector of
be the unit Perron eigenvector of 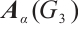 , and
, and 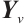 be the entry of
be the entry of 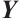 corresponding to the vertex
corresponding to the vertex 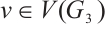 . Since
. Since 
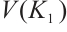 is an equitable partition of
is an equitable partition of 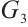 ,
, 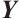 takes the same value on the vertices of
takes the same value on the vertices of 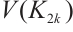 (respectively
(respectively 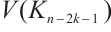 and
and 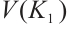 ). Let
). Let  for
for 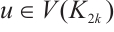 ,
, 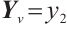 for
for 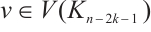 and
and 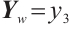 for
for 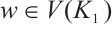 , then
, then 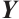 can be written below:
can be written below:
Let 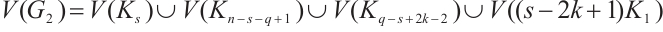 . Then
. Then  can be partitioned as
can be partitioned as
where 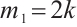 ,
, 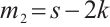 and
and 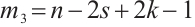 .
.
Thus, by 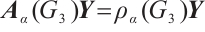 , we can get that
, we can get that
Hence, it follows from Eqs. (1) and (2) that
which implies 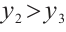 .
.
According to the Rayleigh quotient, we derive that
Thus, 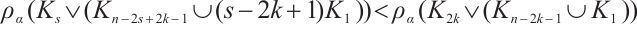 .
.
Moreover, we prove that 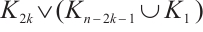 is not
is not 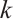 -extendable. Set
-extendable. Set 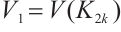 ,
, 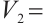
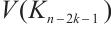 and
and 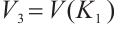 , we take a nonempty subset
, we take a nonempty subset 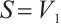 , then
, then 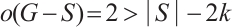 . Hence, Lemma 1 deduces that
. Hence, Lemma 1 deduces that 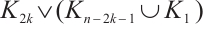 is not
is not 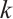 -extendable. Therefore, the proof is completed.
-extendable. Therefore, the proof is completed.
3 Proof of Theorem 2
In this section, we will present a comprehensive proof of Theorem 2.
Proof of Theorem 2 Suppose, by a contradiction, that 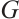 is not
is not 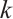 -extendable. We will prove that if
-extendable. We will prove that if 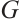 is connected balanced bipartite but not
is connected balanced bipartite but not 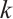 -extendable, then
-extendable, then 
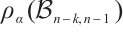 with equality holds if and only if
with equality holds if and only if 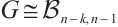 .
.
Let  be a connected balanced bipartite graph, where
be a connected balanced bipartite graph, where  . Since
. Since 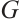 is not
is not 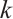 -extendable, by Lemma 3, there exists some nonempty subset
-extendable, by Lemma 3, there exists some nonempty subset  such that
such that 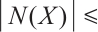
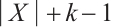 and
and 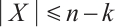 . Let
. Let 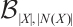 be the connected balanced bipartite graph be obtained from
be the connected balanced bipartite graph be obtained from 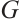 by joining
by joining 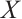 and
and 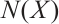 as well as joining
as well as joining  and
and 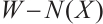 , and by adding all possible edges between
, and by adding all possible edges between  and
and 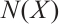 , i.e.,
, i.e., 
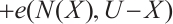 .
.
For convenience, we may set 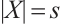 . It is clear then that
. It is clear then that 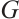 is a spanning subgraph of
is a spanning subgraph of 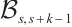 , and
, and
By Lemma 2, we can deduce that
with equality holds if and only if 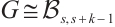 .
.
If  or
or 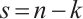 , then
, then  , which is the claimed extremal graph. By the symmetry of
, which is the claimed extremal graph. By the symmetry of 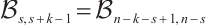 , we need to prove
, we need to prove 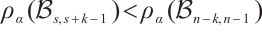 for
for  .
.
Let  be the unit Perron eigenvector of
be the unit Perron eigenvector of 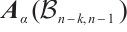 , and
, and 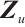 denotes the entry of
denotes the entry of  corresponding to the vertex
corresponding to the vertex 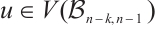 . It is easy to see that
. It is easy to see that 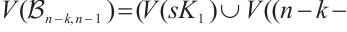
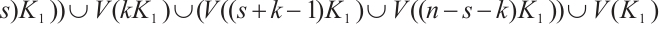 is an equitable partition of
is an equitable partition of 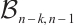 , and so, all vertices of
, and so, all vertices of 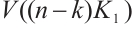 (respectively
(respectively 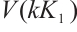 ,
,  and
and 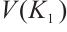 ) have the same entries in
) have the same entries in  . Then we may set
. Then we may set 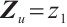 for
for 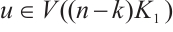 ,
, 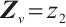 for
for  ,
, 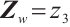 for
for 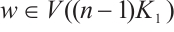 and
and 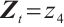 for
for 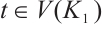 , respectively. So, we write
, respectively. So, we write
Let 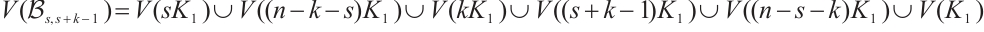 . Then one can partition
. Then one can partition 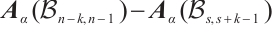 as follows:
as follows:
where 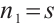 ,
, 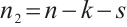 ,
, 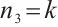 and
and 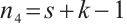 .
.
Thus, by 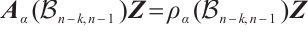 , we can get
, we can get
Now, from Eq. (3) we have
Moreover, by Eqs. (4) and (5) we deduce that
Consequently, combining with Eqs. (6) and (7) we have
which implies that 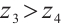 .
.
Moreover, by Rayleigh's principle, we can get
Hence, it deduces that 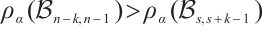 . Note that the graph
. Note that the graph 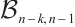 is not
is not 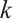 -extendable. Therefore, this completes the proof of Theorem 2.
-extendable. Therefore, this completes the proof of Theorem 2.
References
- Nikiforov V. Merging the A- and Q-spectral theories[J]. Applicable Analysis and Discrete Mathematics, 2017, 11(1): 81-107. [Google Scholar]
- Plummer M D. On n-extendable graphs[J]. Discrete Mathematics, 1980, 31(2): 201-210. [Google Scholar]
- Plummer M D. Toughness and matching extension in graphs[J]. Discrete Mathematics, 1988, 72(1): 311-320. [Google Scholar]
- Plummer M D. Matching extension and the genus of a graph[J]. Journal of Combinatorial Theory, Series B, 1988, 44(3): 329-337. [Google Scholar]
- Ananchuen N, Caccetta L. Matching extension and minimum degree[J]. Discrete Mathematics, 1997, 170(1/2/3): 1-13. [Google Scholar]
- Lou D J, Yu Q L. Connectivity of k-extendable graphs with large k[J]. Discrete Applied Mathematics, 2004, 136(1): 55-61. [Google Scholar]
- Chen C P. Binding number and toughness for matching extension[J]. Discrete Mathematics, 1995, 146(1/2/3): 303-306. [Google Scholar]
- Robertshaw A M, Woodall D R. Binding number conditions for matching extension[J]. Discrete Mathematics, 2002, 248(1/2/3): 169-179. [Google Scholar]
- Maschlanka P, Volkmann L. Independence number in n-extendable graphs[J]. Discrete Mathematics, 1996, 154(1/2/3): 167-178. [Google Scholar]
- Ananchuen N, Caccetta L. A note of k-extendable graphs and independence number[J]. Australasian Journal of Combinatorics, 1995, 12: 59-65. [Google Scholar]
- Fan D D, Lin H Q. Spectral conditions for k-extendability and k-factors of bipartite graphs[EB/OL]. [2024-03-08]. https://doi.org/10.48550/arXiv.2211.09304. [Google Scholar]
- Zhou S Z, Zhang Y L. Signless Laplacian spectral radius for a k-extendable graph[EB/OL]. [2024-03-08]. https://doi.org/10.48550/arXiv.2303.16687. [Google Scholar]
- Zhang Y K, van Dam E R. Matching extension and distance spectral radius[J]. Linear Algebra and Its Applications, 2023, 674: 244-255. [Google Scholar]
- Plummer M D. Matching extension in bipartite graphs[J]. Congressus Numerantium, 1986, 54 : 245-258. [Google Scholar]
- Zhao Y H, Huang X Y, Wang Z W. The A-spectral radius and perfect matchings of graphs[J]. Linear Algebra and Its Applications, 2021, 631: 143-155. [Google Scholar]
All Figures
 |
Fig. 1 The extremal graph 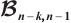
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.