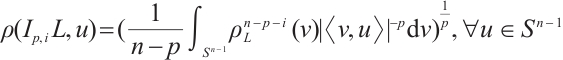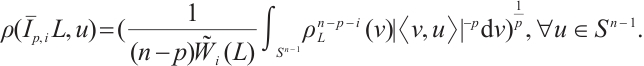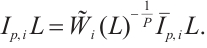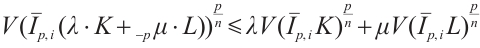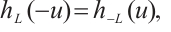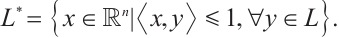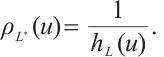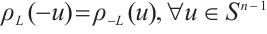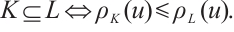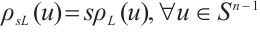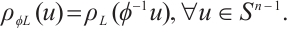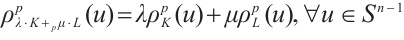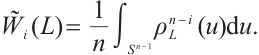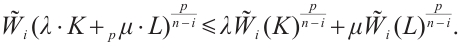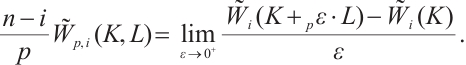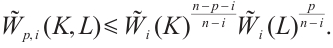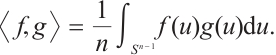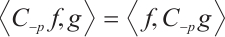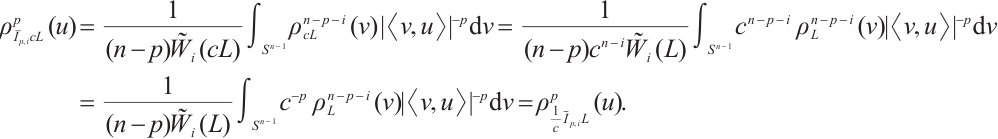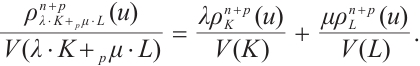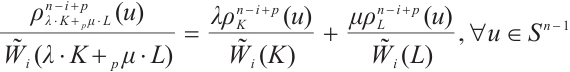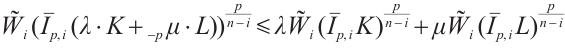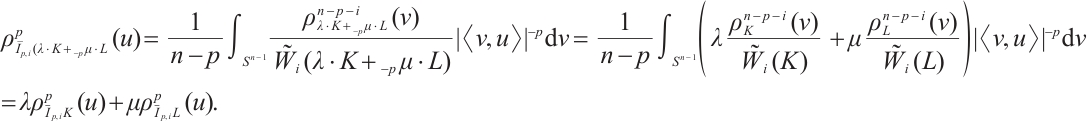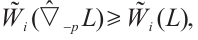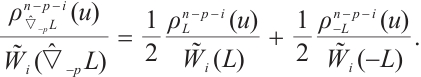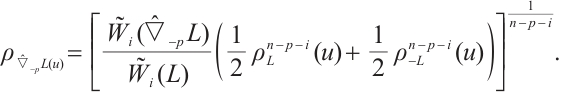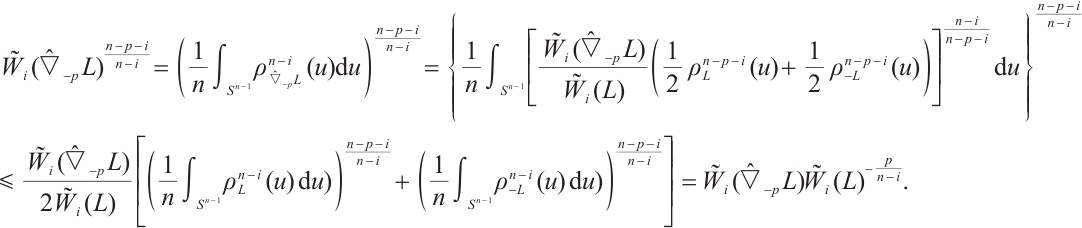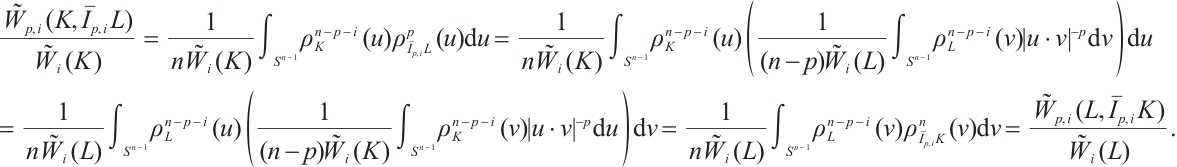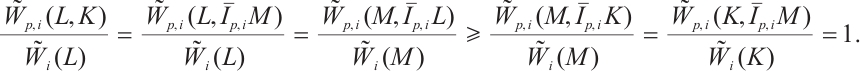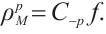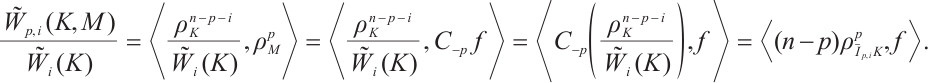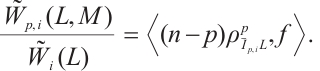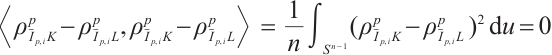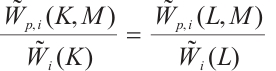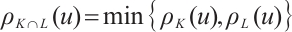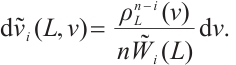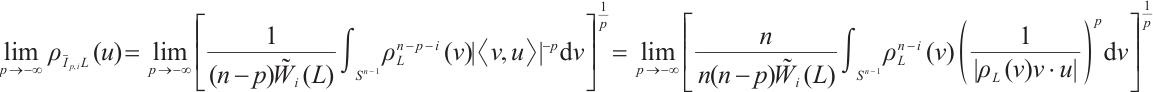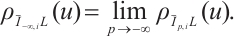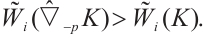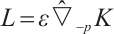| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 2, April 2025
|
|
|---|---|---|
| Page(s) | 125 - 132 | |
| DOI | https://doi.org/10.1051/wujns/2025302125 | |
| Published online | 16 May 2025 | |
Mathematics
CLC number: O175
The Normalized Lp Mixed Intersection Bodies
规范化的Lp混合相交体
School of Mathematics and Computational Science, Hunan University of Science and Technology, Xiangtan 411201, Hunan, China
Received:
23
June
2024
In this paper, we introduce the normalized  mixed intersection body and demonstrate how the normalized
mixed intersection body and demonstrate how the normalized  mixed intersection body operator can be used to obtain the polar body operator as a limit. Moreover, we study the
mixed intersection body operator can be used to obtain the polar body operator as a limit. Moreover, we study the  -Busemann-Petty type problem for the normalized
-Busemann-Petty type problem for the normalized 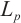 mixed intersection bodies.
mixed intersection bodies.
摘要
我们介绍了规范化的 混合相交体并且证明了如何使用规范化的
混合相交体并且证明了如何使用规范化的 混合相交体得到作为极限的极体算子。此外,我们研究了规范化的
混合相交体得到作为极限的极体算子。此外,我们研究了规范化的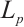 混合相交体的
混合相交体的 -Busemann-Petty型问题。
-Busemann-Petty型问题。
Key words: mixed intersection / radial function / the Minkowski inequality / Lp-Busemann-Petty type problem
关键字 : 混合相交体 / 径向函数 / Minkowski不等式 / Busemann-Petty型问题
Cite this article: LI Xiaohui, LIU Lijuan. The Normalized Lp Mixed Intersection Bodies[J]. Wuhan Univ J of Nat Sci, 2025, 30(2): 125-132.
Biography: LI Xiaohui, female, Master candidate, research direction: convex geometry. E-mail: lixiaohui992024@163.com
Foundation item: Supported by the Postgraduate Scientific Research Innovation Project of Hunan Province (CX20231033)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
The setting for this paper is  -dimensional Euclidean space
-dimensional Euclidean space  . Denote by
. Denote by  and
and 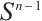 the unit ball and its boundary in
the unit ball and its boundary in  , respectively. If
, respectively. If 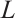 is a star-shaped set with respect to the origin in
is a star-shaped set with respect to the origin in 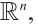 then its radial function
then its radial function 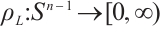 is defined, for
is defined, for  , by
, by
And 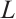 is called a star body about the origin if
is called a star body about the origin if 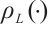 is continuous and positive. Denote by
is continuous and positive. Denote by 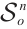 the class of star bodies about the origin in
the class of star bodies about the origin in 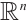 and by
and by 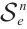 the class of origin-symmetric star bodies in
the class of origin-symmetric star bodies in 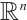 .
.
Intersection bodies were first named by Lutwak[1] and have been intensively studied[2-13]. With the advent of the 21st century, the research on intersection bodies has expanded in scope, encompassing a broader range of disciplines[14-23]. Haberl and Ludwig[24] defined a characterization of  intersection bodies. Berck[25] studied the convexity of the
intersection bodies. Berck[25] studied the convexity of the 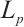 -intersection bodies of origin-symmetric convex bodies. Wang and Li[26] extended the general
-intersection bodies of origin-symmetric convex bodies. Wang and Li[26] extended the general  intersection bodies and settled its Busemann-Petty type problem. Intersection bodies have been identified as crucial in solving the Busemann-Petty type problem[2,8,11,13,21-22,26].
intersection bodies and settled its Busemann-Petty type problem. Intersection bodies have been identified as crucial in solving the Busemann-Petty type problem[2,8,11,13,21-22,26].
If  is a star body, then the intersection body,
is a star body, then the intersection body, 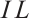 , of
, of 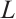 is defined as follows. Its radial function in the direction
is defined as follows. Its radial function in the direction  equals the
equals the 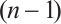 -dimensional volume of
-dimensional volume of 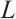 section by
section by 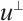 , i.e., for all
, i.e., for all  ,
, 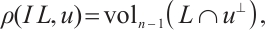
 where
where  denotes the hyperplane orthogonal to
denotes the hyperplane orthogonal to 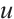 .
.
Liu and Wang[27] extended the 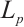 intersection bodies to
intersection bodies to 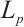 mixed intersection bodies. If
mixed intersection bodies. If 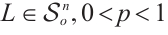 (or
(or 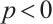 ) and
) and 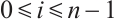 , then the
, then the 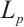 mixed intersection body,
mixed intersection body, 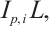 of
of 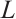 is an origin-symmetric star body, whose radial function is as follows,
is an origin-symmetric star body, whose radial function is as follows,
In this paper, we first define the normalized  mixed intersection body as follows. If
mixed intersection body as follows. If 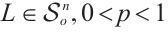 (or
(or 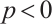 ) and
) and 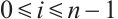 , then the normalized
, then the normalized 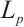 mixed intersection body,
mixed intersection body, 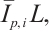 of
of 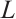 is an origin-symmetric star body, whose radial function is defined by
is an origin-symmetric star body, whose radial function is defined by
From (2) and (3), we have
One aim of this paper is to research the dual Brunn-Minkowski inequality for the normalized 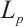 mixed intersection bodies in
mixed intersection bodies in 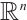 .
.
Theorem 1 If 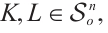 and
and 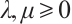 (not both zero),
(not both zero), 
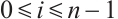 , then
, then
with the equality holds if 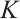 is a dilation of
is a dilation of 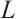 . If
. If 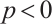 , the inequality (4) is reversed. Let
, the inequality (4) is reversed. Let 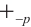 denotes the
denotes the 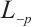 harmonic Blaschke radial sum.
harmonic Blaschke radial sum.
Studying the normalized  Busemann-Petty problem is another aim of this paper.
Busemann-Petty problem is another aim of this paper.
Theorem 2 Let 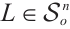 and
and 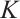 be a normalized
be a normalized 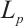 mixed intersection body,
mixed intersection body, 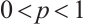 (or
(or  ), and
), and 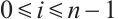 . If
. If 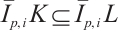 , then
, then 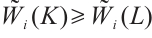 , with the equality holds if and only if
, with the equality holds if and only if 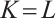 .
.
1 Notation and Preliminaries
We refer to Schneider's works as a general source on the theory of convex (star) bodies [19].
Denote by 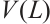 the volume of the compact set
the volume of the compact set  in
in 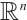 and by
and by 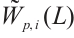 the
the 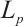 dual mixed quermassintegrals of the compact set
dual mixed quermassintegrals of the compact set 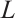 in
in 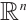 .
.
If 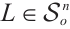 , then the support function, hL, of L is defined by hL(u)=max{〈x,u〉,x∈L},∀u∈Sn-1. Hence,
, then the support function, hL, of L is defined by hL(u)=max{〈x,u〉,x∈L},∀u∈Sn-1. Hence,
where 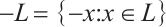 .
.
If 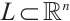 is a convex body with the origin in its interior, then the polar body,
is a convex body with the origin in its interior, then the polar body, 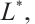 of
of 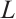 is defined by
is defined by
Obviously, for all  (see Ref. [19]),
(see Ref. [19]),
For  , according to the definition of the radial function, then we have
, according to the definition of the radial function, then we have
If 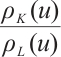 is independent of
is independent of  , then say the star body
, then say the star body 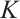 is a dilation of
is a dilation of 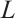 . Let
. Let 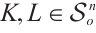 , for all
, for all  ,
,
If 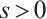 , then we have
, then we have
If  then we have
then we have
Let 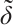 denote the radial Hausdorff metric. If
denote the radial Hausdorff metric. If 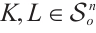 , then
, then 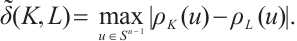
A sequence 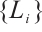 of star bodies converges to
of star bodies converges to  if
if 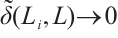 , as
, as 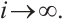 Thus,
Thus,  as
as  if and only if
if and only if 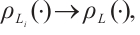 uniformly, as
uniformly, as 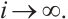
For  , and
, and 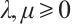 (not both zero), then the
(not both zero), then the  radial sum
radial sum  , is defined by
, is defined by
For 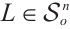 and
and 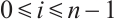 , the dual quermassintegral
, the dual quermassintegral  has the following integral representation:
has the following integral representation:
When  . For
. For  ,
, (not both zero), and
(not both zero), and 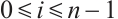 . By using Minkowski integral inequality, if
. By using Minkowski integral inequality, if 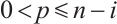 , then we have
, then we have
If 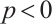 or
or 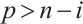 , then the above inequality (13) is reversed. With the equality holds if and only if
, then the above inequality (13) is reversed. With the equality holds if and only if 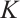 is a dilation of
is a dilation of  .
.
For 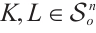 and
and 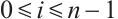 , the
, the  dual mixed quermassintegrals
dual mixed quermassintegrals  is defined by
is defined by
The integral representation of the  dual mixed quermassintegrals
dual mixed quermassintegrals  is defined by
is defined by
When 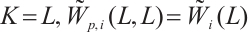 , by using Hölder inequality, the
, by using Hölder inequality, the 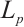 dual mixed Minkowski inequality is established in Ref. [28].
dual mixed Minkowski inequality is established in Ref. [28].
For 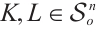 and
and 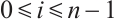 , if
, if  , then
, then
If 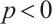 or
or 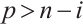 , then the above inequality (15) is reversed. With the equality holds if and only if
, then the above inequality (15) is reversed. With the equality holds if and only if 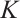 is a dilation of
is a dilation of 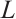 .
.
Denote by 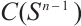 the class of real-valued, continuous functions on
the class of real-valued, continuous functions on 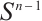 , by
, by 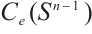 the subset of
the subset of 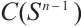 being the even functions, and by
being the even functions, and by 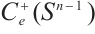 the subset of
the subset of 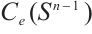 being the nonnegative functions. Assume
being the nonnegative functions. Assume 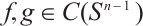 , then
, then 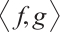 is defined by
is defined by
Let 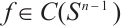 and
and 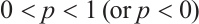 , then the
, then the 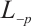 cosine transform,
cosine transform,  , of
, of 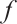 is defined by (see Ref. [29])
is defined by (see Ref. [29])
It is easy to verify that the linear transformation  is self-adjoint (see Ref. [26]), i.e., if
is self-adjoint (see Ref. [26]), i.e., if 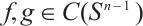 , then
, then
By (3) and (1), then we have
2 Main Results
Lemma 1 If 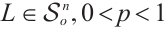 (or
(or 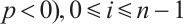 and
and 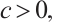 then
then 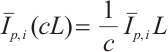 .
.
Proof From (3), and (9), we obtain that
The harmonic Blaschke radial sum was first introduced by Lutwak[30], and the  analog was introduced by Wang and Zhang[31]. Let
analog was introduced by Wang and Zhang[31]. Let  , and
, and 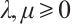 (not both zero),
(not both zero), 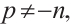 the
the 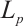 harmonic Blaschke radial sum,
harmonic Blaschke radial sum, 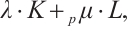 is defined by, for all
is defined by, for all  ,
,
Similarly, if 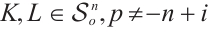 , and
, and 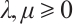 (not both zero), the generalized
(not both zero), the generalized 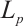 harmonic Blaschke radial sum,
harmonic Blaschke radial sum, 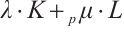 can be stated as
can be stated as
When 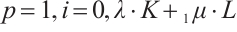 is just the harmonic Blaschke radial sum
is just the harmonic Blaschke radial sum 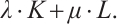
We demonstrate that the following  dual mixed Brunn-Minkowski inequality is more general than Theorem 1.
dual mixed Brunn-Minkowski inequality is more general than Theorem 1.
Theorem 3 If 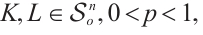
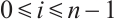 , and
, and 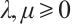 , then
, then
with the equality holds if  is a dilation of L. If
is a dilation of L. If 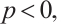 then the above inequality is reversed.
then the above inequality is reversed.
Proof From (3) and (21), for all  , we have
, we have
If 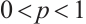 , then
, then  . By (12), (23), and Minkowski integral inequality, it follows that
. By (12), (23), and Minkowski integral inequality, it follows that
If 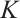 and
and 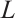 are dilations of each other, then there exists a constant c, such that
are dilations of each other, then there exists a constant c, such that  . By Lemma 1, then we have
. By Lemma 1, then we have  for all
for all  . This means that
. This means that  and
and 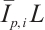 are dilations of each another. From the equality condition of Minkowski integral inequality, the equality in (24) holds if
are dilations of each another. From the equality condition of Minkowski integral inequality, the equality in (24) holds if 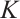 is a dilation of L.
is a dilation of L.
When 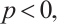 we get
we get  and the inequality in (22) is reversed.
and the inequality in (22) is reversed.
When 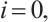 Theorem 3 is Theorem 1. For brevity, let
Theorem 3 is Theorem 1. For brevity, let 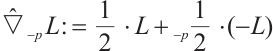 .
.
Lemma 2 If 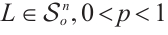 (or
(or 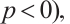 and
and  , then
, then
with the equality holds if and only if  is origin-symmetric.
is origin-symmetric.
Proof By (21), one can obtain
Equivalently,
Since 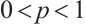 and
and 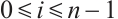 , it follows from (12), (26), and Minkowski integral inequality that
, it follows from (12), (26), and Minkowski integral inequality that
Thus, 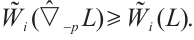
From the equality condition of Minkowski integral inequality, we see that equality holds if and only if 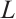 and
and  are dilations of each other, which means that
are dilations of each other, which means that 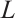 is the origin-symmetric star body.
is the origin-symmetric star body.
Trivially, we can obtain the same result if  .
.
Lemma 3 If 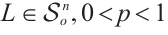 (or
(or  and
and  , then
, then 
Proof From (3), (7), and (26), we have that, for all  ,
,
Lemma 4 If 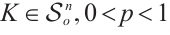 (or
(or 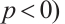 and
and  , for all
, for all 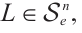 then
then 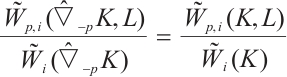 .
.
Proof By (7), (14), and (26), we see that
The following result is necessary to prove Theorem 2.
Theorem 4 If 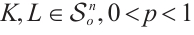 (or
(or 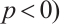 and
and 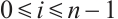 , then
, then  .
.
Proof From (3), (14), and Fubini's theorem, we obtain that
The following normalized  -Busemann-Petty problem is considered in this paper. Suppose
-Busemann-Petty problem is considered in this paper. Suppose 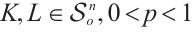 (or
(or 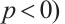 and
and 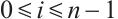 . If
. If 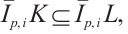 is it true that
is it true that 
As in the case of the classical Busemann-Petty problem, we will demonstrate that if  is a normalized
is a normalized 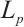 mixed intersection body, then the normalized
mixed intersection body, then the normalized  -Busemann-Petty problem has an affirmative answer.
-Busemann-Petty problem has an affirmative answer.
Proof of Theorem 2 Let 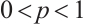 and
and 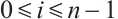 . If
. If 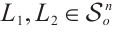 and
and 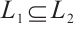 , then
, then 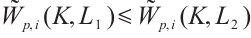 .
.
Since 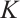 is a normalized
is a normalized 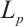 mixed intersection body, there exists a star body
mixed intersection body, there exists a star body 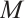 such that
such that 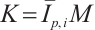 . By Theorem 4 and the hypothesis of Theorem 2, we obtain that
. By Theorem 4 and the hypothesis of Theorem 2, we obtain that
By (13), we have that  with the equality holds if and only if
with the equality holds if and only if  is a dilation of L.
is a dilation of L.
If 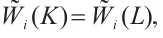 then
then 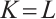 . When
. When  , the result is also obtained.
, the result is also obtained.
In the next step, we will characterize the equality of the normalized 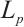 mixed intersection in terms of the normalized
mixed intersection in terms of the normalized 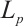 dual mixed quermassintegrals.
dual mixed quermassintegrals.
Theorem 5 If 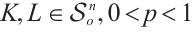 (or
(or 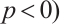 and
and 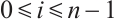 , then
, then 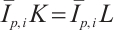 if and only if
if and only if
for all  .
.
Proof According to Lemma 3 and Lemma 4, we can assume that 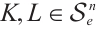 .
.
On one hand, let the equality (27) holds for all  . Suppose
. Suppose 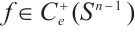 and
and 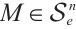 by
by
By (14), (16), (18), (19), and (28), we have
Similarly,
Thus, for all 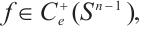
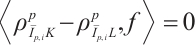 .
.
The above equation must holds for all 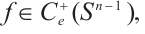 since any function in
since any function in 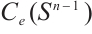 as the difference of two functions in
as the difference of two functions in 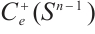 . If we take
. If we take 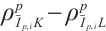 for
for 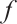 , then we have
, then we have
Hence, 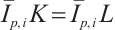 .
.
On the other hand, suppose 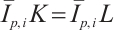 . If
. If 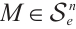 satisfying
satisfying 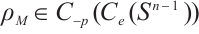 , then there exists
, then there exists 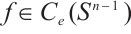 such that
such that 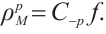
By (29), (30), and the fact that 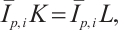 we have
we have
for all  satisfying
satisfying  . Since
. Since 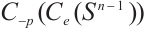 is dense in
is dense in 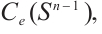 and
and 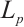 dual mixed quermassintegrals are continuous for all
dual mixed quermassintegrals are continuous for all 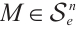 , then the above equality (31) holds for all
, then the above equality (31) holds for all 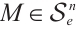 .
.
Next, we show that the operator 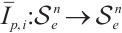 is injective.
is injective.
Theorem 6 Let 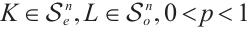 (or
(or  and
and 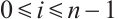 . If
. If  then
then 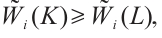 with equality if and only if
with equality if and only if  .
.
Proof By taking 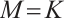 in Theorem 5, we have
in Theorem 5, we have 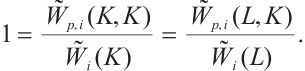
If 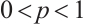 and
and 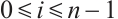 , then by (15), we have
, then by (15), we have 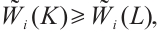 with equality if and only if
with equality if and only if 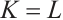 .
.
Trivially, the result is also obtained if 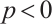 .
.
If  are two star bodies, then
are two star bodies, then
Let 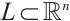 be a convex body which contains the origin in its interior. Note that the point
be a convex body which contains the origin in its interior. Note that the point 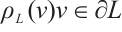 for every
for every 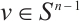 . Thus,
. Thus, 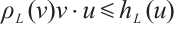 for all
for all  , and there exists a point
, and there exists a point  , such that
, such that 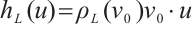 . Then
. Then
Since 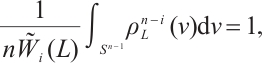 the dual mixed cone-quermassintegrals probability measure of
the dual mixed cone-quermassintegrals probability measure of 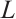 on
on  is expressed as follows:
is expressed as follows:
From (3), (5), (7), (32), (33), and (34), we have
Suppose that  is a convex body with the origin in its interior, we define
is a convex body with the origin in its interior, we define 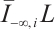 by, for all
by, for all  ,
,
If 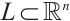 is a convex body with the origin in its interior, by (35) and (36), then
is a convex body with the origin in its interior, by (35) and (36), then 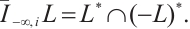
Specifically, if  is an origin-symmetric convex body in
is an origin-symmetric convex body in  , then
, then 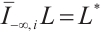 .
.
Remark 1 Suppose that 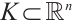 is a convex body which contains the origin in its interior. If
is a convex body which contains the origin in its interior. If  then
then 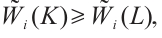 with equality if and only if
with equality if and only if 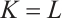 .
.
The answer to the normalized 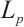 -Busemann-Petty problem is negative if
-Busemann-Petty problem is negative if 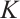 is not origin-symmetric.
is not origin-symmetric.
Theorem 7 If 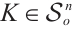 is not origin-symmetric,
is not origin-symmetric, 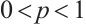 (or
(or 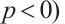 and
and 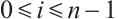 , then there exists an origin-symmetric star body
, then there exists an origin-symmetric star body 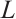 such that
such that  but
but  .
.
Proof By Lemma 2 and that 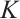 is not origin-symmetric, we have
is not origin-symmetric, we have
Set
where
From (37) and (39), we have
By (38), Lemma 1, Lemma 3, and (40), we have
But from (37), (38), and (39), we have
References
- Lutwak E. Intersection bodies and dual mixed volumes[J]. Advances in Mathematics, 1988, 71(2): 232-261. [Google Scholar]
- Li C, Wang W D. Brunn-Minkowski inequalities of general Lp-intersection bodies[J]. Wuhan University Journal of Natural Sciences, 2021, 26(1): 1-7. [Google Scholar]
- Gardner R J. Intersection bodies and the Busemann-petty problem[J]. Transactions of the American Mathematical Society, 1994, 342(1): 435-445. [Google Scholar]
- Zheng Y P, Jiang X Y, Chen X T, et al. On some generalizations of the Brunn-Minkowski inequality[J]. Linear Algebra and Its Applications, 2020, 586: 103-110. [Google Scholar]
- Zhao C J, Bencze M. Brunn-Minkowski inequality for Lp-mixed intersection bodies[J]. Miskolc Mathematical Notes, 2017, 18(1): 507. [Google Scholar]
- Zhao C J. The multiple radial Blaschke-minkowski homomorphisms[J]. Mathematical Notes, 2023, 114(5): 1381-1400. [Google Scholar]
- Ellmeyer S, Hofstätter G C. Complex L-intersection bodies[J]. Advances in Mathematics, 2023, 431: 109247. [Google Scholar]
- Gardner R J, Koldobsky A, Schlumprecht T. An analytic solution to the Busemann-Petty problem on sections of convex bodies[J]. The Annals of Mathematics, 1999, 149(2): 691-703. [Google Scholar]
- Goodey P, Weil W. Intersection bodies and ellipsoids[J]. Mathematika, 1995, 42(2): 295-304. [Google Scholar]
- Kalton N, Koldobsky A. Intersection bodies and Lp-spaces[J]. Advances in Mathematics, 2019, 196: 257-275. [Google Scholar]
- Koldobsky A. Intersection bodies and the Busemann-Petty problem[J]. Comptes Rendus de L'Académie Des Sciences - Series I - Mathematics, 1997, 325(11): 1181-1186. [Google Scholar]
- Koldobsky A. Intersection bodies in ℝ4[J]. Advances in Mathematics, 1998, 136(1): 1-14. [Google Scholar]
- Koldobsky A. Intersection bodies, positive definite distributions, and the Busemann-Petty problem[J]. American Journal of Mathematics, 1998, 120(4): 827-840. [Google Scholar]
- Gregory W, Koldobsky A. Inequalities for the derivatives of the Radon transform on convex bodies[J]. Israel Journal of Mathematics, 2021, 246(1): 261-280. [Google Scholar]
- Koldobsky A. A functional analytic approach to intersection bodies[J]. Geometric & Functional Analysis GAFA, 2000, 10(6): 1507-1526. [Google Scholar]
- Berlow K, Brandenburg M C, Meroni C, et al. Correction to: Intersection bodys of polytopes[J]. Beiträge Algebra Geom, 2022, 63(2): 441-443. [Google Scholar]
- Lu F H, Mao W H, Leng G S. On star duality of mixed intersection bodies[J]. Journal of Inequalities and Applications, 2006, 2007(1): 039345. [Google Scholar]
- Berg A, Schuster F E. Lutwak-Petty projection inequalities for Minkowski valuations and their duals[J]. Journal of Mathematical Analysis and Applications, 2020, 490(1): 124190. [Google Scholar]
- Schneider R. Convex Bodies: The Brunn-Minkowski Theory[M]. New York: Cambridge University Press, 2014. [Google Scholar]
- Wang W, He R G, Yuan J. On mixed complex intersection bodies[J]. Math Inequal Appl, 2015, 18: 419-428. [Google Scholar]
- Zhang G Y. A positive solution to the Busemann-Petty problem in ℝ4[J]. The Annals of Mathematics, 1999, 149(2): 535-543. [Google Scholar]
- Wang W D. Busemann-Petty type problem for the general Lp-centroid bodies[J]. Analysis in Theory and Applications, 2023, 39(1): 69-82. [Google Scholar]
- Zhao C J, Leng G S. Brunn-Minkowski inequality for mixed intersection bodies[J]. Journal of Mathematical Analysis and Applications, 2005, 301(1): 115-123. [Google Scholar]
- Haberl C, Ludwig M. A characterization of Lp intersection bodies[J]. International Mathematics Research Notices, 2006, 2006(9): 10548. [MathSciNet] [Google Scholar]
- Berck G. Convexity of Lp-intersection bodies[J]. Advances in Mathematics, 2009, 222: 920-936. [Google Scholar]
- Wang W D, Li Y N. Busemann-Petty problem for general Lp-intersection bodies[J]. Acta Mathematica Sinica, English Series, 2015, 31(5): 777-786. [Google Scholar]
- Liu L J, Wang W. Inequalities for Lp mixed intersection bodies[J]. Chinese Quart J Math, 2018, 33(2): 156-165. [Google Scholar]
- Ma T Y. Lp mixed intersection bodies[J]. J Math Inequal, 2014, 8(3): 559-579. [Google Scholar]
- Grinberg E, Zhang G Y. Convolutions, transforms, and convex bodies[J]. Proceedings of the London Mathematical Society, 1999, 78(1): 77-115. [CrossRef] [MathSciNet] [Google Scholar]
- Lutwak E. Centroid bodies and dual mixed volumes[J]. Proceedings of the London Mathematical Society, 1990, 3(2): 365-391. [Google Scholar]
- Wang W, Zhang N. The normalized Lp intersection bodies[J]. Math Inequal Appl, 2018, 21: 353-367. [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.