Mathematics

CLC number: O175.2

Asymptotic Behavior of Singular Solution to the k-Hessian Equation with a Matukuma-Type Source

College of Science, Xi'an University of Science and Technology, Xi'an 710054, Shaanxi, China

^† Corresponding author. E-mail: wang.biao@xust.edu.cn

Received: 20 November 2023

Abstract

This paper is concerned with radially positive solutions of the 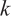$k$-Hessian equation involving a Matukuma-type source 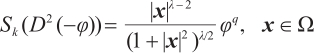$S_k(D^{\mathrm{2}}(-\phi ))=\frac{|\mathit{x}{|}^{\lambda -\mathrm{2}}}{(\mathrm{1}+|\mathit{x}{|}^{\mathrm{2}}{)}^{\lambda /\mathrm{2}}}{\phi }^q,\mathit{x}\in \mathrm{\Omega }$, where 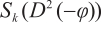$S_k(D^{\mathrm{2}}(-\phi ))$ is the 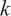$k$-Hessian operator, 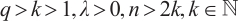$q>k>\mathrm{1},\lambda >\mathrm{0},n>\mathrm{2}k,k\in \mathbb{N}$, and $\mathrm{\Omega }$ 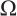is a suitable bounded domain in 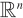${\mathbb{R}}^n$. It turns out that there are two different types of radially positive solutions for 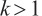$k>\mathrm{1}$, i.e., M-solution (singular at 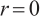$r=\mathrm{0}$) and E-solution (regular at 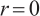$r=\mathrm{0}$), which is distinct from the case when 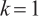$k=\mathrm{1}$. 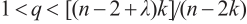For $\mathrm{1}<q<[(n-\mathrm{2}+\lambda )k]/(n-\mathrm{2}k)$, we apply an iterative approach to improve accuracy of asymptotic expansions of M-solution step by step to the desired extend. In contrast to the case 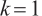$k=\mathrm{1}$, we require a more precise range of parameters due to repeated application of Taylor expansions, which also makes asymptotic expansions need more delicate investigation.