| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 2, April 2025
|
|
|---|---|---|
| Page(s) | 103 - 110 | |
| DOI | https://doi.org/10.1051/wujns/2025302103 | |
| Published online | 16 May 2025 | |
Mathematics
CLC number: O175.28
Time Decay of Linearized Isentropic 2D Bipolar Navier-Stokes-Poisson System
二维线性等熵双极Navier-Stokes-Poisson方程的时间衰减
School of Mathematics, Hohai University, Nanjing 211100, Jiangsu, China
Received:
7
July
2024
Cauchy problem for the linearized bipolar isentropic Navier-Stokes-Poisson system in 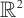 is studied. Through the reformulation of unknown functions, we change the formal system into a linearized Navier-Stokes system and a unipolar Navier-Stokes-Poisson system. Based on a delicate analysis of the corresponding Green function,
is studied. Through the reformulation of unknown functions, we change the formal system into a linearized Navier-Stokes system and a unipolar Navier-Stokes-Poisson system. Based on a delicate analysis of the corresponding Green function, 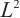 decay estimate of the solution is obtained.
decay estimate of the solution is obtained.
摘要
本文考虑二维空间线性等熵双极Navier-Stokes-Poisson方程的柯西问题。通过对未知函数的重组,我们把原方程组转化成线性的Navier-Stokes和单极Navier-Stokes-Poisson方程组之和。通过对相应格林函数的详细分析,得到解的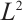 衰减估计。
衰减估计。
Key words: bipolar Navier-Stokes-Poisson system / Green function / L2 decay
关键字 : 双极Navier-Stokes-Poisson方程组 / 格林函数 / L2衰减
Cite this article: XU Hongmei, GUO Xiaoxiao. Time Decay of Linearized Isentropic 2D Bipolar Navier-Stokes-Poisson System[J]. Wuhan Univ J of Nat Sci, 2025, 30(2): 103-110.
Biography: XU Hongmei, female, Associate professor, research direction: partial differential equations. E-mail: xxu_hongmei@163.com
Foundation item: Supported by the National Natural Science Foundation of China (12271141)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


