| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 2, April 2025
|
|
|---|---|---|
| Page(s) | 139 - 149 | |
| DOI | https://doi.org/10.1051/wujns/2025302139 | |
| Published online | 16 May 2025 | |
Mathematics
CLC number: O241
Numerical Integration of the Function with Twin Boundary Layers
带有双边界层函数的数值积分
School of Mathematical Sciences, Suzhou University of Science and Technology, Suzhou 215009, Jiangsu, China
† Corresponding author. E-mail: ycheng@usts.edu.cn
Received:
28
May
2024
Traditional numerical integration requires sufficient smoothness of the integrand to achieve high-order algebraic accuracy. If the function has a boundary layer with large gradient, the composite integration formula on the uniform mesh will produce very large integration errors. In this paper, we study the Newton-Cotes formula based on Lagrange interpolation functions, local 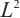 projection approximating the integrand, and Gauss integration. On the Shishkin mesh, we establish an optimal-order integration error estimate uniformly in the perturbation parameter. The convergence rate is the same as that for the smooth function. Numerical experiments confirm the sharpness of our theoretical results.
projection approximating the integrand, and Gauss integration. On the Shishkin mesh, we establish an optimal-order integration error estimate uniformly in the perturbation parameter. The convergence rate is the same as that for the smooth function. Numerical experiments confirm the sharpness of our theoretical results.
摘要
传统的数值积分需要被积函数具有较高的光滑性以获得高阶代数精度。当函数具有大梯度变化的双边界层时,基于均匀网格的复化积分公式将产生较大的积分误差。本文研究三类数值积分公式,即基于拉格朗日基函数的牛顿-科特斯公式、被积函数基于局部L2投影近似以及经典的高斯积分。借助于分片一致的Shishkin网格,证明了与小参数无关的最优阶积分误差估计,该收敛阶与光滑函数数值积分收敛阶相同。数值实验证实了我们的理论结果。
Key words: boundary layers / Shishkin mesh / Newton-Cotes formula / local L2 projection / Gauss integration
关键字 : 边界层 / Shishkin网格 / 牛顿-科特斯公式 / 局部L2-投影 / 高斯积分
Cite this article: KANG Juan, CHENG Yao. Numerical Integration of the Function with Twin Boundary Layers[J]. Wuhan Univ J of Nat Sci, 2025, 30(2): 139-149.
Biography: KANG Juan, female, Master candidate, research direction: numerical analysis of the differential equations. E-mail: kangjuan@post.usts.edu.cn
Foundation item: Supported by the National Natural Science Foundation of China (11801396), Natural Science Foundation of Jiangsu Province (BK20170374), Qing Lan Project of Jiangsu University and Graduate Student Scientific Research Innovation Projects of Jiangsu Province (KYCX24_3407)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


