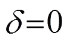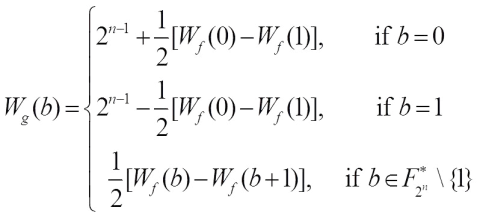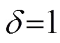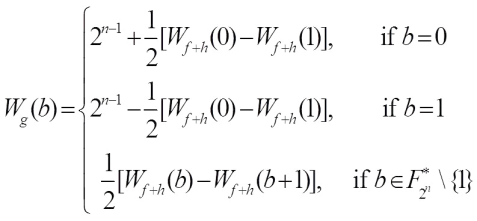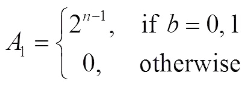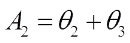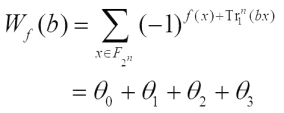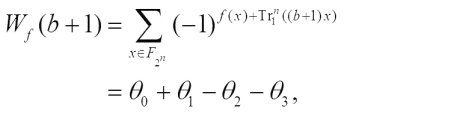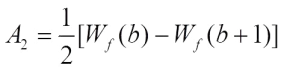| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 26, Number 6, December 2021
|
|
|---|---|---|
| Page(s) | 453 - 458 | |
| DOI | https://doi.org/10.1051/wujns/2021266453 | |
| Published online | 17 December 2021 | |
Mathematics
CLC number: O29
The Walsh Transform of a Class of Boolean Functions
1 School of Mathematical Sciences, Huaibei Normal University, Huaibei 235000, Anhui, China
2 School of Cyber Science, University of Science and Technology of China, Hefei 230027, Anhui, China
3 School of Computer Engineering, Bengbu University, Bengbu 233030, Anhui, China
† To whom correspondence should be addressed. E-mail: cglbox@sina.com
Received: 4 August 2021
The Walsh transform is an important tool to investigate cryptographic properties of Boolean functions. This paper is devoted to study the Walsh transform of a class of Boolean functions defined as 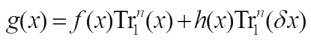 , by making use of the known conclusions of Walsh transform and the properties of trace function, and the conclusion is obtained by generalizing an existing result.
, by making use of the known conclusions of Walsh transform and the properties of trace function, and the conclusion is obtained by generalizing an existing result.
Key words: Boolean function / Walsh transform / trace function
Biography: JIANG Niu, female, Master candidate, research direction: cryptography. E-mail: 1401471403@qq.com
Foundation item: Supported by the Natural Science Foundation of Anhui Higher Education Institutions of China (KJ2020ZD008) , Key Research and Development Projects in Anhui Province (202004a05020043) and the Graduate Innovation Fund of Huaibei Normal University (yx2021022)
© Wuhan University 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Boolean functions are important objects in discrete mathematics. They play a role in symmetric cryptography and error-correcting coding theory, and they also have a significant influence on the design and analysis of cryptographic algorithms. The Walsh transform is a vital tool to investigate cryptographic properties of Boolean functions. Some important properties of cryptographic functions, such as resiliency and nonlinearity can be characterized by their Walsh transform[1-3]. An interesting problem is to find Boolean functions with few Walsh transform values and determine their distributions.
Bent functions introduced by Rothaus[4] in 1976 are interesting combinatorial objects with maximum Hamming distance to the set of all affine functions, but they cannot be used in cryptography directly since they exist only in an even number of variables and are not be balanced. Such functions have been extensively studied because of their important applications in coding theory[5,6], cryptography[7], and sequence designs[8]. To get balanced functions with high nonlinearity in odd or even number of variable, Carlet[9] generalized the bent functions to plateaued functions and they take Walsh transform values 0, 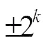 for a fixed positive integer k. Semi-bent, as a particular case, is an important kind of Boolean functions with three Walsh transform values. In Ref. [10], some classes of Boolean functions with four-valued Walsh spectra are presented by complementing the values of bent functions at two points, one of which is zero and the other is nonzero, and their Walsh spectrum distributions are determined finally. Inspired by this work, recently Jin et al[11] presented three classes of Boolean functions with six-valued Walsh spectra, which were derived from bent functions by complementing their values at the zero and another two nonzero points, and determined their Walsh spectrum distributions with a similar method. In Ref. [12], some classes of Boolean functions with five Walsh transform values were presented by adding the product of two or three linear functions into some known bent functions, and their Walsh spectrum distributions were determined finally. In Ref. [13], Tang et al gave a generic construction of bent functions defined as
for a fixed positive integer k. Semi-bent, as a particular case, is an important kind of Boolean functions with three Walsh transform values. In Ref. [10], some classes of Boolean functions with four-valued Walsh spectra are presented by complementing the values of bent functions at two points, one of which is zero and the other is nonzero, and their Walsh spectrum distributions are determined finally. Inspired by this work, recently Jin et al[11] presented three classes of Boolean functions with six-valued Walsh spectra, which were derived from bent functions by complementing their values at the zero and another two nonzero points, and determined their Walsh spectrum distributions with a similar method. In Ref. [12], some classes of Boolean functions with five Walsh transform values were presented by adding the product of two or three linear functions into some known bent functions, and their Walsh spectrum distributions were determined finally. In Ref. [13], Tang et al gave a generic construction of bent functions defined as 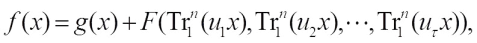 where n=2m, g(x) is any known bent function over
where n=2m, g(x) is any known bent function over 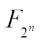 satisfying some conditions,
satisfying some conditions, 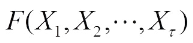 is an arbitrary polynomial in
is an arbitrary polynomial in 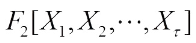 . In particular, the cases of
. In particular, the cases of 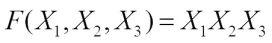 and
and 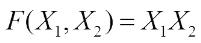 have been studied by Xu et al[12] and Mesnager[14], respectively. The purpose of this paper is to present the Walsh transform of the Boolean function defined as
have been studied by Xu et al[12] and Mesnager[14], respectively. The purpose of this paper is to present the Walsh transform of the Boolean function defined as 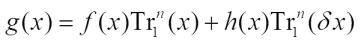 (1) where f(x) and h(x) are Boolean functions over
(1) where f(x) and h(x) are Boolean functions over  and
and  . In particular, the case of
. In particular, the case of 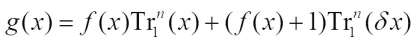 (2) has been studied by Pang et al[15].
(2) has been studied by Pang et al[15].
This paper is organized as follows. In Section 1, we give some basic concepts and results. In Section 2, we present the Walsh transform of the Eq. (1). In Section 3, we conclude this paper.
1 Preliminaries
Let 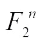 denote the n-dimensional vector space over F2, and
denote the n-dimensional vector space over F2, and 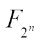 denote the finite field with 2n elements. For any set E,
denote the finite field with 2n elements. For any set E, 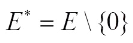 . By viewing each
. By viewing each  as a vector
as a vector 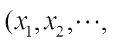
 where
where 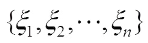 is a basis of
is a basis of 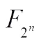 over F2, we identify
over F2, we identify 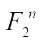 with
with 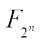 and then every function
and then every function 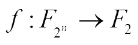 is equivalent to a Boolean function. For
is equivalent to a Boolean function. For  , the inner product is defined as
, the inner product is defined as  .
.
For any positive integer k|n, the trace function from 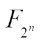 to
to 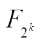 is the mapping defined as
is the mapping defined as 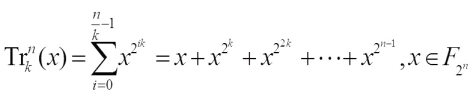 When k=1,
When k=1, 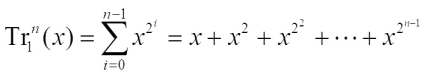 is called the absolute trace function.
is called the absolute trace function.
Some important and useful properties of the trace function are provided in the following:
1) 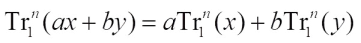 ,
, 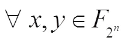 and
and  .
.
2) 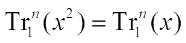 for any
for any 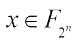 .
.
3) For any 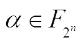 ,
, 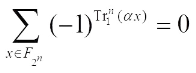 if
if  .
.
4) When 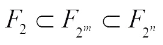 , the trace function
, the trace function 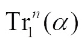 satisfies the transitivity property, that is,
satisfies the transitivity property, that is,  .
.
5) For any 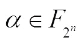 ,
, 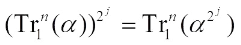 ,
, 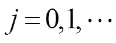 .
.
Let f be a Boolean function from 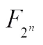 to F2, and the set of which is denoted by Bn. The Walsh transform of
to F2, and the set of which is denoted by Bn. The Walsh transform of 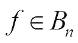 at
at 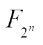 is defined as
is defined as 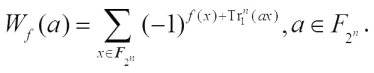
The values 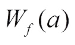 ,
,  are called the Walsh coefficients of f. The Walsh spectrum of a Boolean function f is the multiset
are called the Walsh coefficients of f. The Walsh spectrum of a Boolean function f is the multiset 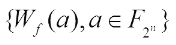 . A Boolean function f is said to be balanced if
. A Boolean function f is said to be balanced if 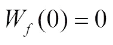 .
.
The nega-Hadamard transform of f(x) at  is the complex valued function
is the complex valued function 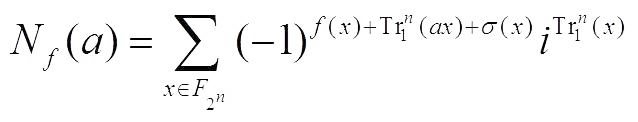 where
where 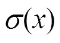 is the function defined by
is the function defined by 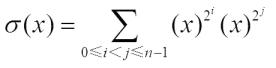 . A function
. A function 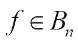 is negabent if
is negabent if 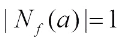 for all
for all  .
.
2 Main Results
Let n be a positive integer and f be a Boolean function from 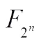 to F2. For any
to F2. For any  , the Boolean function
, the Boolean function 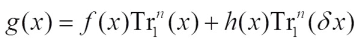 can be written as
can be written as where
where  for
for  .
.
The relationship between 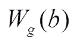 and
and 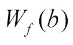 ,
,  ,
, 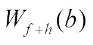 is given in Theorem 1.
is given in Theorem 1.
Theorem 1 Let  ,
,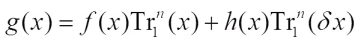 Then, the Walsh transform of g(x) at
Then, the Walsh transform of g(x) at  is given by
is given by
3) When 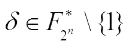 ,
,
Proof For simplicity, denote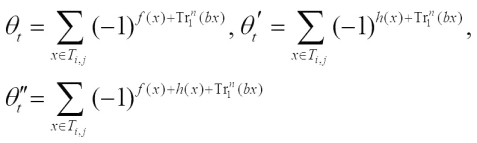 where
where 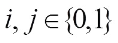 ,
, 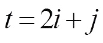 ,
, 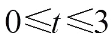 .
.
The proof proceeds in terms of three cases: 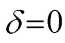 ,
, 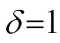 and
and 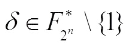 .
.
1) If 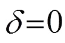 , then one obtains
, then one obtains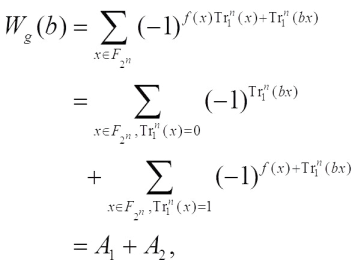 where
where 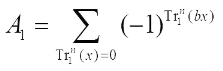 ,
, 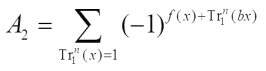 .
.
2) The proof of 2) is obvious from 1).
3) If 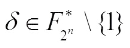 , then one obtains
, then one obtains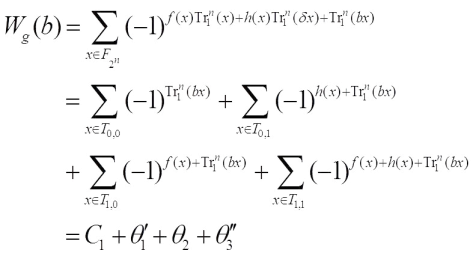 where
where 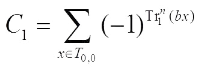 .
.
Note that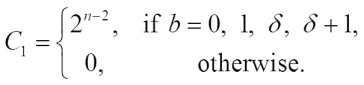 Together with the fact
Together with the fact and
and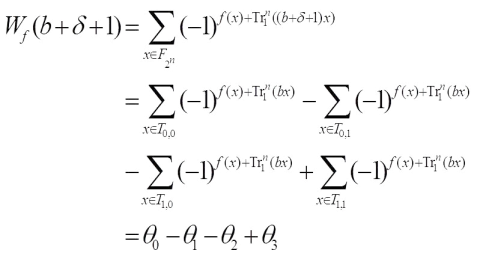 Similarly,
Similarly,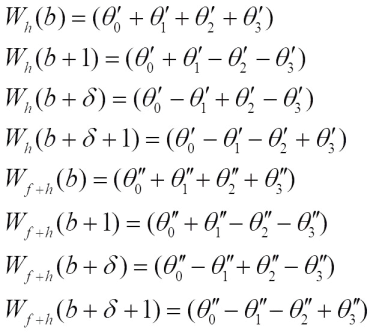 Then by
Then by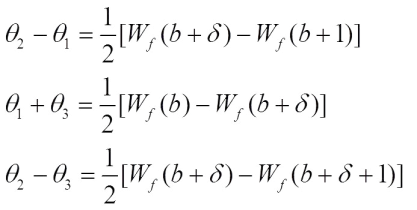 we have
we have by
by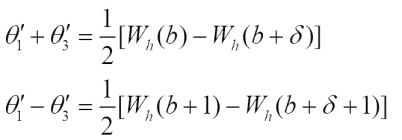 we have
we have Similarly, we have
Similarly, we have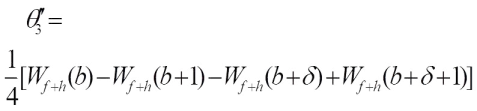 One immediately gets that
One immediately gets that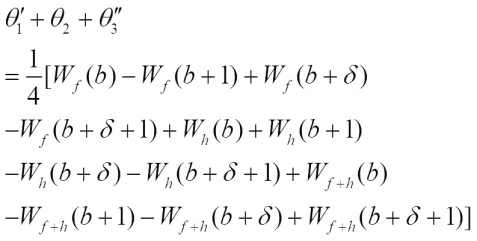 when b=0,
when b=0,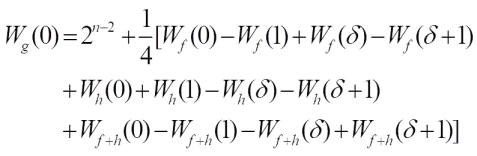 when b=1,
when b=1,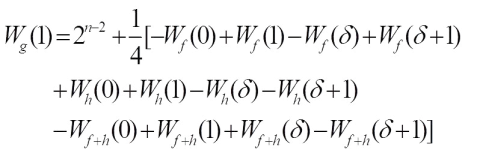 when
when  ,
,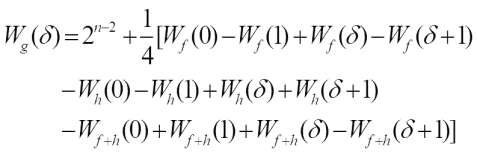 when
when 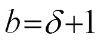 ,
,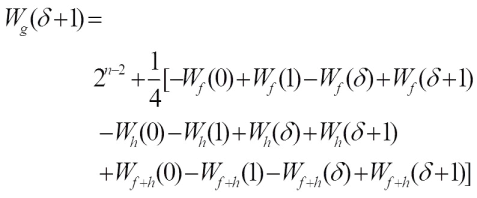 The proof is completed.
The proof is completed.
In particular, when 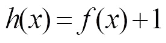 , the function
, the function 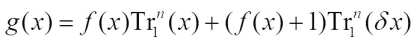 is exactly the ones studied by Pang et al[15]. Note that our generic construction works for any f(x) and h(x). Therefore, our construction contains the previous ones in Ref. [15] as special cases.
is exactly the ones studied by Pang et al[15]. Note that our generic construction works for any f(x) and h(x). Therefore, our construction contains the previous ones in Ref. [15] as special cases.
Corollary 1 Let 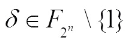 , and
, and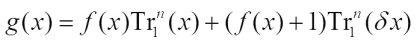 The Walsh transform of g(x) at
The Walsh transform of g(x) at  is given by
is given by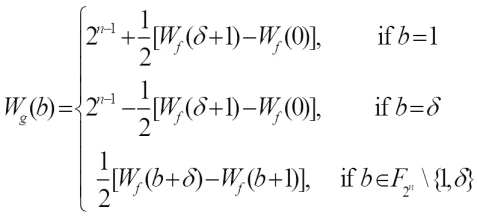 In the following, pang proposed three new classes of Boolean functions having the form as Eq. (2) by suitable choices of f(x). The first class is obtained from bent functions, including Dillon bent, kasami bent and Gold-like bent functions, and from the definition of the dual of bent functions, the Walsh transform value distribution of such class is presented. Ref. [15] indicates that the Walsh spectrum distribution of g(x) derived from bent functions is obtained from calculating the dual function of f and the values of
In the following, pang proposed three new classes of Boolean functions having the form as Eq. (2) by suitable choices of f(x). The first class is obtained from bent functions, including Dillon bent, kasami bent and Gold-like bent functions, and from the definition of the dual of bent functions, the Walsh transform value distribution of such class is presented. Ref. [15] indicates that the Walsh spectrum distribution of g(x) derived from bent functions is obtained from calculating the dual function of f and the values of 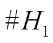 ,
, 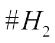 and
and 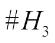 . Therefore, the Walsh spectrum distribution of
. Therefore, the Walsh spectrum distribution of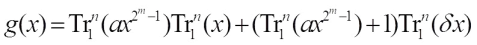 is presented.
is presented.
The second class is derived from Gold functions 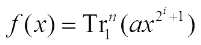 and their Walsh spectrum distribution is obtained by making use of the Walsh transform property of Gold functions and the known conclusions of Weil sums in characteristic 2. The Walsh spectrum distribution of g(x) which is obtained by Gold functions is discussed in the following three cases.
and their Walsh spectrum distribution is obtained by making use of the Walsh transform property of Gold functions and the known conclusions of Weil sums in characteristic 2. The Walsh spectrum distribution of g(x) which is obtained by Gold functions is discussed in the following three cases.
Case 1 n/d is even and 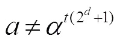 for any integer t. It is known that in this case
for any integer t. It is known that in this case 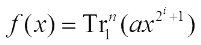 is bent. Then the Walsh spectrum distribution of
is bent. Then the Walsh spectrum distribution of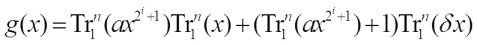 is given in Ref. [15].
is given in Ref. [15].
Case 2 n/d is even and 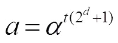 for some integer t. In this case the Walsh spectrum distribution of
for some integer t. In this case the Walsh spectrum distribution of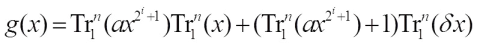 depends on whether
depends on whether 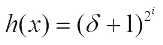 is solvable.
is solvable.
Case 3 n/d is odd. In this case we only need to consider 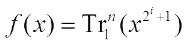 , then the Walsh spectrum distribution of
, then the Walsh spectrum distribution of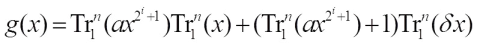 is presented in Ref. [15].
is presented in Ref. [15].
The last class comes from the product of linearized polynomials which have three or four Walsh transform values. With the help of k-tuple balance property, the Walsh spectrum distribution of such functions are determined. Ref. [15] present the Walsh transform of 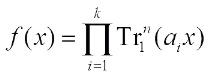 together with the Walsh transform of Eq. (2), the Walsh spectrum distribution of
together with the Walsh transform of Eq. (2), the Walsh spectrum distribution of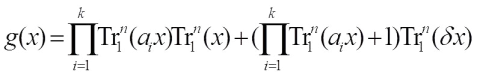 is given.
is given.
In another particular case, when f(x)=0 and  , the function
, the function 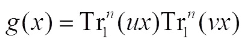 is studied by Wu et al[16]. They give the necessary and sufficient conditions for g(x) to be negabent.
is studied by Wu et al[16]. They give the necessary and sufficient conditions for g(x) to be negabent.
Corollary 2 Let 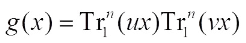 , where
, where 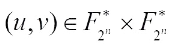 . Then g(x) is negabent on
. Then g(x) is negabent on 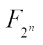 if and only if one of the following conditions is satisfied:
if and only if one of the following conditions is satisfied:
1) 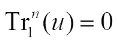 and
and 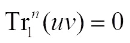 .
.
2) 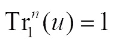 and
and 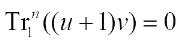 .
.
In Ref. [16], first they presented the necessary and sufficient conditions for the functions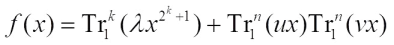 to be negabent, where n=2k,
to be negabent, where n=2k, 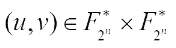 ,
, 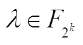 , when
, when 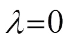 it is the one discussed in Ref. [16]. Further, by using some permutation trinomials over
it is the one discussed in Ref. [16]. Further, by using some permutation trinomials over 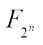 , they presented some classes of negabent functions of the form
, they presented some classes of negabent functions of the form where 0<k<n.
where 0<k<n.
3 Conclusion
In this paper, we proposed the Walsh transform of a class of Boolean functions by using the properties of the Walsh transform and the trace function. Then, we hope that we can deduce the Walsh spectrum distributions of g(x) defined as Eq. (1) by suitable choices of f(x) and h(x). Further, several new classes of Boolean functions with few Walsh transform values are obtained.
References
- Carlet C, Mesnager S. Four decades of research on bent functions [J]. Designs, Codes and Cryptography, 2016, 78(1): 5-50. [Google Scholar]
- Mesnager S. On Semi-Bent Functions and Related Plateaued Functions over the Galois Field [M]. Berlin: Springer-Verlag, 2014. [Google Scholar]
- Tu Z B, Zheng D B, Zeng X Y, et al. Boolean functions with two distinct Walsh coefficients [J]. Applicable Algebra in Engineering Communication and Computing, 2011, 22(5-6): 359-366. [Google Scholar]
- Rothaus O S. On “bent” functions [J]. Journal of Combinatorial Theory, 1976, 20(3): 300-305. [Google Scholar]
- Frances M, Litman A. On covering problems of codes [J]. Theory of Computing Systems, 1997, 30(2): 113-119. [CrossRef] [MathSciNet] [Google Scholar]
- Calderbank R, Kantor W M. The geometry of two-weight codes [J]. Bulletin of the London Mathematical Society, 1986, 18(2): 97-122. [Google Scholar]
- Carlet C. Boolean functions for cryptography and error-correcting codes [J]. Encyclopedia of Mathematics and Its Applications, 2016, 78(1): 5-50. [Google Scholar]
- Olsen J, Scholtz R, Welch L. Bent-function sequences [J]. IEEE Transactions on Information Theory, 1982, 28(6): 858-864. [CrossRef] [MathSciNet] [Google Scholar]
- Carlet C. Boolean and vectorial plateaued functions and APN functions [J]. IEEE Transactions on Information Theory, 2015, 61(11): 6272-6289. [CrossRef] [MathSciNet] [Google Scholar]
- Sun Z Q, Hu L. Boolean functions with four-valued Walsh spectra [J]. Journal of Systems Science and Complexity, 2015, 28(3): 743-754. [CrossRef] [MathSciNet] [Google Scholar]
- Jin W G, Du X N, Sun Y Z, et al. Boolean functions with six-valued Walsh spectra and their application [J]. Cryptography and Communications, 2021, 13(5): 393-405. [Google Scholar]
- Xu G K, Cao X W, Xu S D. Several new classes of Boolean functions with few Walsh transform values [J]. Applicable Algebra in Engineering Communication and Computing, 2017, 28(2): 155-176. [Google Scholar]
- Tang C M, Zhou Z C, Qi Y F, et al. Generic construction of bent functions and bent idempotents with any possible algebraic degrees [J]. IEEE Transactions on Information Theory, 2017, 63(10): 6149-6157. [CrossRef] [MathSciNet] [Google Scholar]
- Mesnager S. Several new infinite families of bent functions and their duals [J]. IEEE Transactions on Information Theory, 2014, 60(7): 4397-4407. [CrossRef] [MathSciNet] [Google Scholar]
- Pang T T, Li N, Zhang L, et al. Several new classes of (balanced) Boolean functions with few Walsh transform values [J]. Advances in Mathematics of Communications, 2021, 15(4): 757-775. [Google Scholar]
- Wu G F, Li N, Zhang Y Q, et al. Several classes of negabent functions over finite fields [J]. Science China. Information Sciences, 2018, 61(3): 1-3. [CrossRef] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.