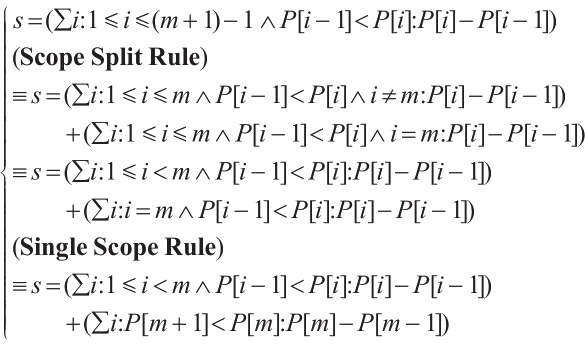© Wuhan University 2022

0 Introduction

The development of reliable software has become a critical point on which we should concentrate, particularly for systems with high safety requirements, such as aerospace control systems and medical equipment systems. Even minor errors in these systems can result in massive losses^[1].

Formal methods are mathematically based techniques for specifying, developing, and testing computer software and hardware systems. Their mathematical basis is the formal logic systems consisting of formal languages, semantics, and proof systems. Formal methods are increasingly being used with appropriate levels of rigor at various stages of a computing system's lifecycle. It contributes significantly to reliability and security of software^[2-4].

Algorithm program correctness is the key to software security. However, programmers often write code intuitively. They hope that if there are small misjudgements, those errors will be exposed in the test. The algorithm obtained in this way is very error-prone. It may cause some hidden issues with software security^[5]. Automatic algorithm programming model has the potential to improve the reliability and efficiency of algorithm program development.

Automatic algorithm programming model consists of three core processes: specification generation, program refinement, and formal verification. Among the three processes, specification generation uses formal methods to describe user requirements; program refinement turns a specification into an executable program by gradually lowering the level of abstraction; and formal verification verifies the correctness of abstract programs generated during program refinement.

The process of specification generation is relatively simple. As a result, in the following, we would introduce a variety of automatic algorithm programming models based on Dijkstra's weakest precondition method^[6-8], Morgan's refinement calculus^[9-12] and PAR(Partition and Recur) method^[13] from the two core processes of program refinement and formal verification. In program refinement, the three methods all provide formal refinement rules, with Morgan's refinement calculus rules being the most numerous. However, only PAR method implements the complete program refinement process, from program specification to executable program(C++ program). In formal verification, the three methods all generate verification conditions manually and then perform manual verification. You et al^[14] enhanced the PAR method by replacing manual verification with mechanical verification via Isabelle. Table 1 compares the above mentioned automatic algorithm programming models in terms of program refinement and formal verification.

The current automatic programming model has two flaws. The first is the incompleteness of program refinement, and the second is the inadequate automation of formal verification. This paper presents an automatic algorithm programming model based on improved Morgan's refinement calculus to address these two issues. For the first deficiency, Morgan's refinement calculus is extended by adding quantifier specification transformation rules, and the C++ generation system is designed and implemented to complete the refinement process from specification to executable program. For the second deficiency, verification conditions are generated automatically based on VCG and mechanically verified by Isabelle. This is a significant step toward achieving high reliability and automation of the verification process.

1 Automatic Algorithm Programming Model

The flow chart of automatic algorithm programming model proposed in this paper is shown in Fig. 1.

Fig. 1 Flow chart of automatic algorithm programming model

1.1 Specification Generation

By analyzing user requirements, we generate an initial formal specification with pre- and post-conditions in specification generation. In this model, the specification is written as w:[P,Q]^[10], where P is the precondition, Q is the postcondition, and w is the list of frame variables. The variables whose values may change, i.e. those in the list w above, are called the frame variables (or, more concisely, simply the frame) of the specification. The code that satisfies the specification w:[P,Q] may only change the value of one or more variables in w.

1.2 Specification Simplification

The generated specification could always be simplified to a lower complexity equivalent specification based on the analysis of concrete features of the specific field. We adopt the methods of problem division and specification transformation to simplify the specification.

1.3 Abstract Program Refinement Method

Definition 1(Sat) Sat(C,w:[P,Q]) is a predication that asserts the IMP(Imperative Programming Language) program C satisfies the specification w:[P,Q].

To make this idea more formal, the assertion that means X is refined by Y (or, equivalently, Y is a refinement of X) is denoted by X ⊆ Y, which is defined as follows^[10].

Definition 2(Refinement) w:[P,Q] ⊆ w:[P',Q'] if and only if

∀C:IMP·Sat(C , w:[P',Q']) => Sat(C , w:[P,Q]).

Thus w:[P,Q] is refined by w:[P',Q'] if every IMP program that satisfies the specification w:[P',Q'] also satisfies the specification w:[P,Q].

The process of abstraction program refinement begins with the specification and ends with the abstract program (IMP program). Each step of the process adheres to the rules for demonstrating correctness. If these rules are applied strictly, we could end up with a correct IMP program^[11].

In this model, the refinement of the abstract program is based on Morgan's refinement calculus. Morgan's refinement calculus provides refinement calculus rules for transforming one specification into another specification or an IMP statement. However, appropriate rules must be chosen by analyzing the specification. In one word, the specification should always be transformed in an equivalent manner to match the appropriate rules.

The Morgan's refinement calculus rules^[6] used in this model are shown in Table 2.

Quantifiers are used in specification to describe the preconditions and postconditions, but the refinement rules outlined above are insufficient to refine such specifications. In this model, we add some quantifier specification transformation rules, as shown in Table 3(Q_a is a quantifier, q_a is the binary operation corresponding to Q_a), which are used to transform the precondition or postcondition equivalently. The formalization of program refinement is optimized by expanding the available formal rules.

1.4 Formal Verification

Artificial analysis during the refinement of an abstract program may result in program errors. Therefore, formal verification is required to ensure the correctness of the IMP program^[12]. Formal verification is divided into two steps. First, based on VCG, verification conditions are generated automatically by the IMP program. Second, the verification conditions are mechanically verified by Isabelle.

1.4.1 VCG

Hoare logic provability could be reduced to assertion language provability. In particular, if we want to prove a Hoare logical triple {P}c{Q}, we can compute an assertion A from it, and then {P}c{Q} is provable if A is provable. A is referred to as a verification condition, and the function that computes A is referred to as a verification condition generator, or VCG ^[15].

The precondition and postcondition are provided as annotations to the VCG for all algorithm programs, and the invariant is additionally provided for WHILE loops. Figure 2 depicts the VCG code template for generating verification conditions.

Fig. 2 VCG code template for generating verification conditions

The advantage of using VCG is that no human or machine is required to know the Hoare logic when trying to prove the generated validation conditions^[15].

1.4.2 Isabelle theorem prover

Isabelle^[16-19] is an auxiliary theorem prover who provides theorem proving with strong theoretical and technical support. Compared with other traditional theorem provers, the Isabelle theorem prover has the following distinguishing features. 1) Isabelle can handle multiple object logics. 2) Isabelle is in favor of new logic, which could be implemented by defining object logic's concrete syntax, abstract syntax, and inference rules. 3) Isabelle's verification language is Isar. It could accurately describe the system under test. Furthermore, Isar benefits from a wide range of data types, logic systems, and so on. 4) The editing tool jEdit could verify each step in the theorem proof, and display the proof status in the output panel.

1.5 IMP Program Refinement

We propose IMP program refinement to improve the completeness of program refinement. This refinement allows for the conversion of formally verified IMP programs to executable C++ programs. As a result, an automatic system known as the C++ generation system^[20-22] is created, and the overall structure of the system is depicted in Fig. 3.

Fig. 3 The overall structure of the C++ generation system

The system mainly consists of four modules: lexical analysis, syntactic analysis, semantic analysis and program transformation.

Lexical analysis transforms the IMP program character sequences into equivalent internal symbol sequences using IMP's lexical rules. Syntactic analysis identifies IMP syntactic items from internal symbol sequences using IMP syntax rules. Semantic analysis applies semantic processing to the syntactic items that have been identified. If the results of the above three analyses are incorrect, error messages will be reported in error handling. On the other hand, if the result is correct, the IMP program will be converted into a C++ program.

2 Example: A Stock's Maximum Income

2.1 Generating Problem Specification

2.1.1 Problem description

Suppose you could buy one share or sell your share per day at the stock's closing price. A stock's income is equal to the selling price minus the buying price. The problem with the maximum income of a stock is to calculate the maximum sum of the incomes from all possible trades over n days.

Figure 4 is an example of the volatility of a stock's closing price over n days.

Fig. 4 An example of the volatility of a stock's closing price

2.1.2 Specification generation

The closing price of this stock in n days is stored in the array $P[\mathrm{0}..n-\mathrm{1}](n=p.len,n>\mathrm{1})$. According to the problem description, the essence of solving the problem is to find all the ascending segments P[i..j](P[i] and P[j] are the minimum value and the maximum value of the ascending segment respectively), then calculate the income P[j]-P[i], finally add up the income of each ascending segment and the result of addition is maximum income.

Therefore, the maximum income of a stock in n days could be expressed by maxincome$(n,P)$ as:

$\begin{array}{l}\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(n,P)=(\sum i:\mathrm{1}\le i<j\le n-\mathrm{1}\wedge \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} P[i-\mathrm{1}]>P[i]\wedge P[j]>P[j+\mathrm{1}]\wedge \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} (\forall k:i\le k<j:P[k]\le P[k+\mathrm{1}]):\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} P[i]-P[i-\mathrm{1}])\end{array}$

The expression of the maxincome(n,P) is required when describing the specification of this problem. However, the specification would be complicated due to the complexity of this expression.

2.1.3 Specification simplification

In order to reduce the complexity of the specification, we could simplify the expression of the maxincome$(n,P)$.

P[j]-P[i] equals (P[i+1]-P[i])+(P[i+2]-P[i+1]) +…+ (P[j]-P[j-1]). For example, the incomefrom buying on day n-2 and selling on day n-5 is (P[n-4]-P[n-5])+ (P[n-3]-P[n-4])+(P[n-2]-P[n-3]). Therefore, we could divide the array P[0..n-1] into the n-1 segments P[0,1], P[1,2], P[2,3],…, P[n-2, n-1], i.e. P[i-1,i](1≤i≤n-1). The maximum income could then be calculated by adding the incomes of all ascending segments ^[23]. It is obviously that whether P[i-1,i] is an ascending segment or not is determined by the truth value of P[i-1]<P[i].

Therefore, maxincome$(n,P)$ could be simplified to:

$\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(n,P)=(\sum i:\mathrm{1}\le i\le n-\mathrm{1}\wedge P[i-\mathrm{1}]<P[i]:P[i]-P[i-\mathrm{1}])$. We introduce a variable s to represent the maximum income calculated at some point in the process, then the postcondition of this problem could be expressed as: $s=$maxincome$(n,P)$. Because the income of a stock is calculated from the second day, the precondition is n>1. In conclusion, the specification is as follows:

$s:[n>\mathrm{1},s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(n,P)]$

2.2 Refining Abstract Program

Figure 5 shows the whole process of refining abstract program, where①, ②, …, 14 represent program specifications and I₁, I₂, …, I₆ represent refined IMP statements. The abstract program refinement ends when all of the specifications have been refined into IMP statements.

Fig. 5 Process diagram of abstract program refinement

2.2.1 Choosing the invariantWe introduce a variable m(0<m≤n) to traverse the array P[0..n-1] from left to right. When the subarray P[0..m-1] is traversed, the maximum income maxincome(m,P) could be calculated, as shown in Fig. 6. Therefore the loop invariant could be defined as

inv≡s=maxincome(m,P)$\wedge$0<m≤n, which is similar to the postcondition(post≡s=maxincome(n,P)≡inv$\wedge$m=n), so the program specification could be replaced equivalently by m,s:[n>1,inv$\wedge$m=n]^[16].

Fig. 6 Traversal process of calculating the maximum income

2.2.2 Establishing the invariant

Before we can refine it to a loop, the general pattern for a specification should be something like w:[inv,inv$\wedge$¬G]. The following refinement process is required to get our refined specification into this shape^[10].

According to Sequential Composition Rule, specification ② could be refined as:

$\begin{array}{l}m,s:[n>\mathrm{1},\mathrm{i}\mathrm{n}\mathrm{v}\wedge m=n]\\ (\mathbf{S}\mathbf{e}\mathbf{q}\mathbf{u}\mathbf{e}\mathbf{n}\mathbf{t}\mathbf{i}\mathbf{a}\mathbf{l}\mathbf{C}\mathbf{o}\mathbf{m}\mathbf{p}\mathbf{o}\mathbf{s}\mathbf{i}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\mathbf{R}\mathbf{u}\mathbf{l}\mathbf{e})\\ \subseteq m,s:[n>\mathrm{1},\mathrm{i}\mathrm{n}\mathrm{v}];m,s:[\mathrm{i}\mathrm{n}\mathrm{v},\mathrm{i}\mathrm{n}\mathrm{v}\wedge m=n]\end{array}$(1)

Specification ③ : We could prove that 0<m+1≤n$\wedge$m₀<m+1≤n is true. Thus the specification ③ could be simplified to be viewed as some actions needed to establish the invariant(which must hold before the iteration could start)^[10].

It should not be difficult to see that the assignment of m=1 and s=0 will be a suitable refinement.

We could prove that n>1=>inv[m,s\1,0] is true, thus the specifications ③ are refined as follows:

$\begin{array}{l}m,s:[n>\mathrm{1},\mathrm{i}\mathrm{n}\mathrm{v}]\\ (\mathbf{A}\mathbf{s}\mathbf{s}\mathbf{i}\mathbf{g}\mathbf{n}\mathbf{m}\mathbf{e}\mathbf{n}\mathbf{t}\mathbf{R}\mathbf{u}\mathbf{l}\mathbf{e})\\ \subseteq m,s:=\mathrm{1,0}................{\mathrm{I}}_{\mathrm{1}}\end{array}$(2)

Thus, the result of "Establishing the Invariant" is:

$\begin{array}{l}m,s:[n>\mathrm{1},\mathrm{i}\mathrm{n}\mathrm{v}];m,s:[\mathrm{i}\mathrm{n}\mathrm{v},\mathrm{i}\mathrm{n}\mathrm{v}\wedge m=n]\\ \subseteq m,s:=\mathrm{1,0};m,s:[\mathrm{i}\mathrm{n}\mathrm{v},\mathrm{i}\mathrm{n}\mathrm{v}\wedge m=n]\end{array}$(3)

2.2.3 Refining to create a loop

According to Repetition Rule, specification ④ could be refined to the following loop statement:

$\begin{array}{l}\mathrm{d}\mathrm{o}m\ne n\to ...........................................{\mathrm{I}}_{\mathrm{2}}\\ m,s:[\mathrm{i}\mathrm{n}\mathrm{v}\wedge m\ne n\wedge V_{\mathrm{0}}=V,\mathrm{i}\mathrm{n}\mathrm{v}\wedge \mathrm{0}\le V<V_{\mathrm{0}}]\\ \mathrm{o}\mathrm{d}\end{array}$(4)

where V₀ is the previous value of V.

V is defined as n-m, and m₀ is defined as the previous value of m, so we could get:

$\begin{array}{l}m,s:[\mathrm{i}\mathrm{n}\mathrm{v}\wedge m\ne n\wedge V_{\mathrm{0}}=V,\mathrm{i}\mathrm{n}\mathrm{v}\wedge \mathrm{0}\le V<V_{\mathrm{0}}]\\ \equiv m,s:[\mathrm{i}\mathrm{n}\mathrm{v}\wedge m\ne n\wedge m_{\mathrm{0}}=m,\mathrm{i}\mathrm{n}\mathrm{v}\wedge m_{\mathrm{0}}<m\le n]\end{array}$(5)

All that remains is to refine the body of the loop into code. Intuitively, we could see that m = m +1 is a good choice. Therefore specification ⑥ could be refined as follows:

$\{\begin{array}{l}m,s:[\mathrm{i}\mathrm{n}\mathrm{v}\wedge m\ne n\wedge m_{\mathrm{0}}=m,\mathrm{i}\mathrm{n}\mathrm{v}\wedge m_{\mathrm{0}}<m\le n]\\ (\mathbf{F}\mathbf{o}\mathbf{l}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{i}\mathbf{n}\mathbf{g}\mathbf{A}\mathbf{s}\mathbf{s}\mathbf{i}\mathbf{g}\mathbf{n}\mathbf{m}\mathbf{e}\mathbf{n}\mathbf{t}\mathbf{R}\mathbf{u}\mathbf{l}\mathbf{e})\\ \subseteq m,s:[\mathrm{i}\mathrm{n}\mathrm{v}\wedge m\ne n\wedge m_{\mathrm{0}}=m,(\mathrm{i}\mathrm{n}\mathrm{v}\wedge m_{\mathrm{0}}<m\le n)[m\backslash m+\mathrm{1}]];\\ m:=m+\mathrm{1}.............................................................{\mathrm{I}}_{\mathrm{3}}\end{array}$(6)

After the above refinement, we have obtained the IMP statement (IMP statement I₁) that changes m, so we remove m from the frame variable. The specification is then updated as follows:

$\{\begin{array}{l}s:[s=(\sum i:\mathrm{1}\le i\le m-\mathrm{1}\wedge P[i-\mathrm{1}]<P[i]:\\ P[i]-P[i-\mathrm{1}])\wedge P[m]>P[m-\mathrm{1}],\\ s=(\sum i:\mathrm{1}\le i\le (m+\mathrm{1})-\mathrm{1}\wedge P[i-\mathrm{1}]<P[i]:\\ P[i]-P[i-\mathrm{1}])]\end{array}$(7)

It is obvious that inv$\wedge$m≠n=>inv$\wedge$m≠n$\wedge$m₀=m is true, so:

$\{\begin{array}{l}s:[\mathrm{i}\mathrm{n}\mathrm{v}\wedge m\ne n\wedge m_{\mathrm{0}}=m,\mathrm{i}\mathrm{n}\mathrm{v}[m\backslash m+\mathrm{1}]\wedge m_{\mathrm{0}}<m+\mathrm{1}\le n]\\ (\mathbf{W}\mathbf{e}\mathbf{a}\mathbf{k}\mathbf{e}\mathbf{n}\mathbf{P}\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{d}\mathbf{i}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\mathbf{R}\mathbf{u}\mathbf{l}\mathbf{e})\\ \subseteq s:[\mathrm{i}\mathrm{n}\mathrm{v}\wedge m\ne n,\mathrm{i}\mathrm{n}\mathrm{v}[m\backslash m+\mathrm{1}]\wedge m_{\mathrm{0}}<m+\mathrm{1}\le n]\\ (\mathrm{i}\mathrm{n}\mathrm{v}\equiv s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P)\wedge \mathrm{0}<m\le n)\\ =s:[s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P)\wedge \mathrm{0}<m\le n\wedge m\ne n,\\ s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m+\mathrm{1},P)\wedge \mathrm{0}<m+\mathrm{1}\le n\wedge m_{\mathrm{0}}<m+\mathrm{1}\le n]\end{array}$(8)

Specifications ⑧$\to$ specifications ⑨, specifications ⑨ $\to$ specifications ⑩:

We could prove that 0<m+1≤n$\wedge$$m_{\mathrm{0}}$<m+1≤n is true. Thus the specification ⑧ could be simplified to:

$\begin{array}{l}s:[s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P)\wedge \mathrm{0}<m\le n\wedge m\ne n,\\ s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m+\mathrm{1},P)]\end{array}$(9)

The next refinement is:

$\{\begin{array}{l}s:[s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P)\wedge \mathrm{0}<m\le n\wedge m\ne n,\\ s = \mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m+\mathrm{1},P)]\\ (\mathbf{W}\mathbf{e}\mathbf{a}\mathbf{k}\mathbf{e}\mathbf{n}\mathbf{P}\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{d}\mathbf{i}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\mathbf{R}\mathbf{u}\mathbf{l}\mathbf{e})\\ \subseteq s:[s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P),s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m+\mathrm{1},P)]\end{array}$(10)

After observing the pre- and post-conditions of specifications ⑩, we analyze the relationship between maxincome(m,P) and maxincome(m+1,P):

$s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P)\Rightarrow \{\begin{array}{c}s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m+\mathrm{1},P),\\ s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P)\hspace{1em},\end{array}\begin{array}{c}\mathrm{i}\mathrm{f}P[m]>P[m-\mathrm{1}]\\ \mathrm{i}\mathrm{f}P[m]\le P[m-\mathrm{1}]\end{array}$(11)

Therefore, specification ⑩ would be refined as follows:

$\{\begin{array}{l}s:[s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P),s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m+\mathrm{1},P)]\\ (\mathbf{S}\mathbf{e}\mathbf{l}\mathbf{e}\mathbf{c}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}\mathbf{R}\mathbf{u}\mathbf{l}\mathbf{e})\subseteq \\ \mathrm{i}\mathrm{f}P[m]>P[m-\mathrm{1}]\to ...............................................{\mathrm{I}}_{\mathrm{4}}\\ s:[s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P)\wedge P[m]>P[m-\mathrm{1}],\\ \hspace{1em} s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m+\mathrm{1},P)]\\ []P[m]\le P[m-\mathrm{1}]\to \\ s:[s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P)\wedge P[m]\le P[m-\mathrm{1}],\\ \hspace{1em} s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m+\mathrm{1},P)]\\ \mathrm{f}\mathrm{i}\end{array}$(12)

Specification 11 could be updated as follows by substituting maxincome(m,P) with its definition:

$\{\begin{array}{l}s:[s=(\sum i:\mathrm{1}\le i\le m-\mathrm{1}\wedge P[i-\mathrm{1}]<P[i]:\\ P[i]-P[i-\mathrm{1}])\wedge P[m]>P[m-\mathrm{1}],\\ s=(\sum i:\mathrm{1}\le i\le (m+\mathrm{1})-\mathrm{1}\wedge P[i-\mathrm{1}]<P[i]:\\ P[i]-P[i-\mathrm{1}])]\end{array}$(13)

For refinement, there is no suitable Morgan's refinement calculus rule. However, using quantifier specification transformation rules, the postcondition could be transformed into a suitable shape:

$\{\begin{array}{l}s=(\sum i:\mathrm{1}\le i\le (m+\mathrm{1})-\mathrm{1}\wedge P[i-\mathrm{1}]<P[i]:P[i]-P[i-\mathrm{1}])\\ (\mathbf{S}\mathbf{c}\mathbf{o}\mathbf{p}\mathbf{e}\mathbf{S}\mathbf{p}\mathbf{l}\mathbf{i}\mathbf{t}\mathbf{R}\mathbf{u}\mathbf{l}\mathbf{e})\\ \equiv s=(\sum i:\mathrm{1}\le i\le m\wedge P[i-\mathrm{1}]<P[i]\wedge i\ne m:P[i]-P[i-\mathrm{1}])\\ +(\sum i:\mathrm{1}\le i\le m\wedge P[i-\mathrm{1}]<P[i]\wedge i=m:P[i]-P[i-\mathrm{1}])\\ \equiv s=(\sum i:\mathrm{1}\le i<m\wedge P[i-\mathrm{1}]<P[i]:P[i]-P[i-\mathrm{1}])\\ +(\sum i:i=m\wedge P[i-\mathrm{1}]<P[i]:P[i]-P[i-\mathrm{1}])\\ (\mathbf{S}\mathbf{i}\mathbf{n}\mathbf{g}\mathbf{l}\mathbf{e}\mathbf{S}\mathbf{c}\mathbf{o}\mathbf{p}\mathbf{e}\mathbf{R}\mathbf{u}\mathbf{l}\mathbf{e})\\ \equiv s=(\sum i:\mathrm{1}\le i<m\wedge P[i-\mathrm{1}]<P[i]:P[i]-P[i-\mathrm{1}])\\ +(\sum i:P[m+\mathrm{1}]<P[m]:P[m]-P[m-\mathrm{1}])\end{array}$(14)

It is easy to find:

$\begin{array}{l}(\sum i:P[m+\mathrm{1}]<P[m]:P[m]-P[m-\mathrm{1}])\\ \equiv \{\begin{array}{c}P[m]-P[m-\mathrm{1}],\mathrm{i}\mathrm{f}P[m]>P[m-\mathrm{1}]\\ \mathrm{0}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em},\mathrm{i}\mathrm{f}P[m]\le P[m-\mathrm{1}]\end{array}\end{array}$(15)

The specification could then be transformed to:

$\{\begin{array}{l}s:[s=(\sum i:\mathrm{1}\le i\le m-\mathrm{1}\wedge P[i-\mathrm{1}]<P[i]:\\ P[i]-P[i-\mathrm{1}])\wedge P[m]>P[m-\mathrm{1}],\\ s=(\sum i:\mathrm{1}\le i\le m-\mathrm{1}\wedge P[i-\mathrm{1}]<P[i]:\\ P[i]-P[i-\mathrm{1}])+P[m]-P[m-\mathrm{1}]]\end{array}$(16)

We could prove that the following derivation is true.

$\{\begin{array}{l}s=(\sum i:\mathrm{1}\le i\le m-\mathrm{1}\wedge P[i-\mathrm{1}]<P[i]:\\ P[i]-P[i-\mathrm{1}])\wedge P[m]>P[m-\mathrm{1}]\\ \Rightarrow (s=(\sum i:\mathrm{1}\le i\le m-\mathrm{1}\wedge P[i-\mathrm{1}]<P[i]:\\ P[i]-P[i-\mathrm{1}])+P[m]-P[m-\mathrm{1}])[s\backslash s+P[m]-P[m-\mathrm{1}]]\end{array}$(17)

Therefore the specification could be refined as follows:

$\{\begin{array}{l}s:[s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P)\wedge P[m]>P[m-\mathrm{1}],\\ s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m+\mathrm{1},P)]\\ (\mathbf{A}\mathbf{s}\mathbf{s}\mathbf{i}\mathbf{g}\mathbf{n}\mathbf{m}\mathbf{e}\mathbf{n}\mathbf{t}\mathbf{R}\mathbf{u}\mathbf{l}\mathbf{e})\\ \subseteq s:=s+P[m]-P[m-\mathrm{1}].............................{\mathrm{I}}_{\mathrm{5}}\end{array}$(18)

In the same way, specification 12 could be refined as:

$\{\begin{array}{l}s:[s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P)\wedge P[m]\le P[m-\mathrm{1}],\\ s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m+\mathrm{1},P)]\\ (\mathbf{S}\mathbf{k}\mathbf{i}\mathbf{p}\mathbf{R}\mathbf{u}\mathbf{l}\mathbf{e})\\ \subseteq \mathrm{S}\mathrm{K}\mathrm{I}\mathrm{P}............................................................{\mathrm{I}}_{\mathrm{6}}\end{array}$(19)

In conclusion, we could obtain the refinement of specification ⑩(IMP statement I₇) by integrating IMP statement I₄, I₅, I₆:

$\{\begin{array}{l}s:[s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m,P),s=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}(m+\mathrm{1},P)]\\ \subseteq \mathrm{i}\mathrm{f}P[m]>P[m-\mathrm{1}]\to s:=s+P[m]-P[m-\mathrm{1}]...{\mathrm{I}}_{\mathrm{7}}\\ \hspace{1em}[]P[m]\le P[m-\mathrm{1}]\to \mathrm{S}\mathrm{K}\mathrm{I}\mathrm{P}\\ \hspace{1em}\mathrm{f}\mathrm{i}\end{array}$(20)

2.2.4 Putting IMP statements all together

We could now glue all of the pieces(IMP statement I₁,I₂,I₃,I₇) together to get the code in Fig. 7 as a refinement of specification ①.

Fig. 7 IMP program of a stock's maximum income

2.3 Formal Verification through Isabelle Based on VCG

The refinement process of Section 2.2 is accompanied by mathematical proof, ensuring manual reliability. However, it is not automatic and highly reliable. If the IMP program in Section 2.2.4 could be verified using Isabelle and VCG, the reliability of the automatic algorithm programming model could be ensured mechanically.

2.3.1 Automatically generating verification conditions based on VCG

Based on the IMP program obtained in Section 2.2.4, we insert the precondition and postcondition before and after the program respectively, and the loop invariant before the loop statement, as shown in top half of Fig. 8. The verification conditions could then be obtained(3 subgoals in bottom half of Fig. 8).

Fig. 8 Verification conditions generation based on VCG

2.3.2 Mechanically verifying the generated conditions through Isabelle

The second subgoal in Fig. 8 generates two recursions, which can be transformed into two lemmas to assist us in verifying the second subgoal. The verification of the two lemmas is depicted in Fig. 9.

Fig. 9 Verification of the two recursions

The next step is to verify the three subgoals in Fig. 8. After we call the Isabelle code "apply auto", there is only one subgoal to verify. This subgoal could be demonstrated automatically using the tool sledgehammer^[24,25]. Figure 10 depicts the outcome of applying sledgehammer for current verification. We can select the Isar proof code and click on it.

Fig. 10 Tool sledgehammer for auxiliary verification

Figure 11 depicts the overall verification process for all the verification conditions.

Fig. 11 The overall verification process

2.4 Refinement of the IMP Program

Through the C++ generation system, an IMP program could be refined to a C++ program. Figure 12 depicts the refinement process for the problem of a stock's maximum income, with the IMP program successfully verified on the left and the C++ program generated automatically on the right. Figure 13 depicts the testing of generated C++ program.

Fig. 12 Refinement from IMP program to C++ program

Fig. 13 Testing of automatically generated C++ program

3 Conclusion

This paper proposes an automatic algorithm programming model based on the improved Morgan's refinement calculus to improve the automation and reliability of algorithm programming. The model generates the program specifications according to user requirements. It refines step by step with formal verification and generates executable programs automatically with the help of the C++ generation system. An example of a stock's maximum income demonstrates the model's effectiveness. The model in this paper has the following characteristics in general.

1) Morgan's refinement calculus is extended by adding of quantifier specification transformation rules. Therefore, the formalization of program refinement is enhanced.

2) The manual generation of verification conditions for algorithm programs is replaced by the automatic generation. Therefore, formal verification automation is improved.

3) Based on the C++ generation system, abstract IMP programs are refined to executable programs. Therefore, the program refinement is more complete.

The automatic algorithm programming model allows for efficient programming while also ensuring the correctness of the generated program. However, two aspects of future work must be improved. One is to expand the refinement rule library to further optimize Morgan's refinement calculus, and the other is to apply the model to more complex data structures.

References

All Tables

All Figures

	Fig. 1 Flow chart of automatic algorithm programming model
In the text

	Fig. 2 VCG code template for generating verification conditions
In the text

	Fig. 3 The overall structure of the C++ generation system
In the text

	Fig. 4 An example of the volatility of a stock's closing price
In the text

	Fig. 5 Process diagram of abstract program refinement
In the text

	Fig. 6 Traversal process of calculating the maximum income
In the text

	Fig. 7 IMP program of a stock's maximum income
In the text

	Fig. 8 Verification conditions generation based on VCG
In the text

	Fig. 9 Verification of the two recursions
In the text

	Fig. 10 Tool sledgehammer for auxiliary verification
In the text

	Fig. 11 The overall verification process
In the text

	Fig. 12 Refinement from IMP program to C++ program
In the text

	Fig. 13 Testing of automatically generated C++ program
In the text