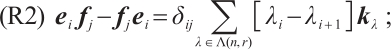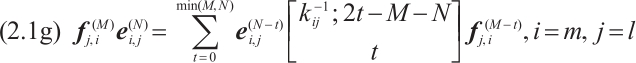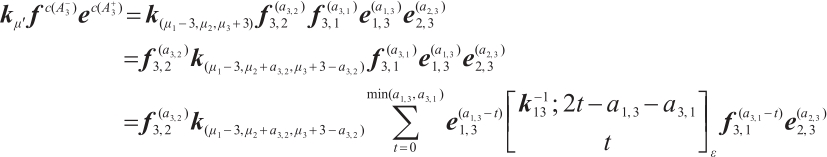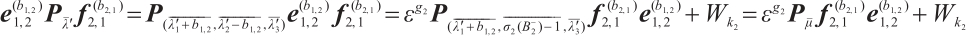| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 28, Number 5, October 2023
|
|
|---|---|---|
| Page(s) | 385 - 391 | |
| DOI | https://doi.org/10.1051/wujns/2023285385 | |
| Published online | 10 November 2023 | |
Mathematics
CLC number: O152.5
The Generators and Relations for Little q-Schur Algebra uk(3,5)
Three Gorges Mathematical Research Center, China Three Gorges University, Yichang 443002, Hubei, China
† To whom correspondence should be addressed. E-mail: yangqian6573@163.com
Received:
18
March
2023
In this paper, we investigate the presentation for little q-Schur algebra  at odd roots. The Poincaré-Birkhoff-Witt (PBW) basis of
at odd roots. The Poincaré-Birkhoff-Witt (PBW) basis of  is obtained through the basis of q-Schur algebra
is obtained through the basis of q-Schur algebra  . Then we present a new set for generators and relations for
. Then we present a new set for generators and relations for  by PBW basis.
by PBW basis.
Key words: q-Schur algebra / little q-Schur algebra / Poincaré-Birkhoff-Witt (PBW) basis / root vectors
Biography: LIU Mingqiang, male, Lecturer, research direction: algebraic groups, quantum groups. E-mail: mingqiangliu@163.com
Fundation item: Supported by the Natural Research Project of Yichang (A23-2-026)
© Wuhan University 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Let 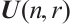 be the q-Schur algebras over
be the q-Schur algebras over  introduced by Dipper and James[1,2], who have showed that q-Schur algebras play an important role in the investigation of presentation theory of the finite general linear groups. Using a geometric setting for q-Schur algebras, Beilinson-Lusztig-MacPherson[3] realized the quantum enveloping algebra
introduced by Dipper and James[1,2], who have showed that q-Schur algebras play an important role in the investigation of presentation theory of the finite general linear groups. Using a geometric setting for q-Schur algebras, Beilinson-Lusztig-MacPherson[3] realized the quantum enveloping algebra  of
of  as a "limit" of q-Schur algebras over
as a "limit" of q-Schur algebras over  , and they defined an epimorphism
, and they defined an epimorphism  from the quantum enveloping algebra
from the quantum enveloping algebra  of
of  to the q-Schur algebras
to the q-Schur algebras  . Then, Du[4] proved that this epimorphism can be applied to any field. For little q-Schur algebras, the definition at odd roots has been obtained, which could be referred to Ref. [5]. Moreover, some results of little q-Schur algebras have been classified in Ref. [6], like simple modules, little q-Schur algebras and finite representation type in the odd roots of unity case. Fu[7] gave the definition of little q-Schur algebras at even unit roots, and explored the related basis and dimension formulas. Therefore, for little q-Schur algebras at any unit roots, the complete classification of representation type has been given by Bian and Liu in Ref. [8].
. Then, Du[4] proved that this epimorphism can be applied to any field. For little q-Schur algebras, the definition at odd roots has been obtained, which could be referred to Ref. [5]. Moreover, some results of little q-Schur algebras have been classified in Ref. [6], like simple modules, little q-Schur algebras and finite representation type in the odd roots of unity case. Fu[7] gave the definition of little q-Schur algebras at even unit roots, and explored the related basis and dimension formulas. Therefore, for little q-Schur algebras at any unit roots, the complete classification of representation type has been given by Bian and Liu in Ref. [8].
In the theory of quantum group, it is an important issue to study the presentation of algebras, in other words, to give a set of generators and relations. In addition, the presentation of q-Schur algebras has been obtained in Refs. [9,10]. It is a natural question to present the little q-Schur algebras. Therefore, the presentations obtained from the perspective of monomial basis for little q-Schur algebras  ,
,  and
and  could be respectively referred to Refs. [11,12]. However, with the increase of r, the relations may become increasingly complex.
could be respectively referred to Refs. [11,12]. However, with the increase of r, the relations may become increasingly complex.
The goal of this paper is to study the generators and relations for little q-Schur algebra  from the perspective of Poincaré-Birkhoff-Witt (PBW) basis which is helpful to investigate the presentation of
from the perspective of Poincaré-Birkhoff-Witt (PBW) basis which is helpful to investigate the presentation of  . We briefly recall the definitions of q-Schur and little q-Schur algebras in Section 1. In Section 2, we prove that the set
. We briefly recall the definitions of q-Schur and little q-Schur algebras in Section 1. In Section 2, we prove that the set 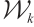 is the basis of little q-Schur algebra
is the basis of little q-Schur algebra  , and present the relations of
, and present the relations of  .
.
1 Preliminary
Let v be an indeterminate and  . For any integers
. For any integers  with
with  , let
, let  ,
,  and
and  . Let
. Let  for
for  . Let
. Let  be a field containing an l'-th primitive root
be a field containing an l'-th primitive root  of unity with
of unity with  . Let
. Let  be defined by
be defined by  . In this paper, we put
. In this paper, we put 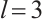 . Specializing
. Specializing  to
to  ,
,  will be viewed as an
will be viewed as an  -module. When
-module. When  is specialized to
is specialized to  ,
,  ,
,  and
and  specialize to
specialize to  ,
,  and
and  .
.
For quantum enveloping algebra of  ,
,  defined on
defined on  has been generated by the elements
has been generated by the elements  ,
,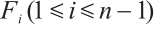 ,
,  ,
,  and satisfies the corresponding relations referred to Section 3.2 of Ref. [13]. Set
and satisfies the corresponding relations referred to Section 3.2 of Ref. [13]. Set  and define the root vectors in
and define the root vectors in  as follows. If
as follows. If  , then set
, then set  ,
, . For
. For  , inductively set
, inductively set  ,
,  . There is an isomorphism
. There is an isomorphism  [14] defined by
[14] defined by  ,
,  ,
,  ,
,  . Then obviously
. Then obviously  .
.
Following Refs. [15,16], let  (respectively,
(respectively, ,
,  ,
,  ) be the
) be the -subalgebra of
-subalgebra of  generated by all
generated by all 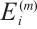 ,
, ,
, and
and  (respectively,
(respectively,  ,
,  ,
,  and
and  ), where for
), where for  ,
,  . Let
. Let
Let  , we denote the image of
, we denote the image of  ,
, 
 in
in  by
by  ,
,  , and
, and  . Let
. Let  be the k-subalgebra of
be the k-subalgebra of  generated by the elements
generated by the elements  ,
,  ,
,  for all i, j. Let
for all i, j. Let  ,
,  ,
,  be the k-subalgebras of
be the k-subalgebras of  generated respectively by the elements
generated respectively by the elements  ,
,  and
and  by Ref. [16].
by Ref. [16].
When  is odd, the elements
is odd, the elements  are the central in
are the central in  . They generate an ideal
. They generate an ideal  of
of  . Let
. Let  and we call
and we call  the infinitesimal quantum group of
the infinitesimal quantum group of  . The presentation for
. The presentation for  was given in Ref. [10]. When
was given in Ref. [10]. When  is even, there is no definition for infinitesimal quantum group of
is even, there is no definition for infinitesimal quantum group of  . Let
. Let 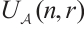 be the algebra over
be the algebra over 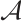 introduced in Ref. [3]. It is shown to be naturally isomorphic to the q-Schur algebra in Ref. [4]. Put
introduced in Ref. [3]. It is shown to be naturally isomorphic to the q-Schur algebra in Ref. [4]. Put  , we shall call
, we shall call  and
and  q-Schur algebras. There is an algebra epimorphism
q-Schur algebras. There is an algebra epimorphism  which could be referred to Refs. [3]. Let
which could be referred to Refs. [3]. Let  and
and  , for
, for  . Moreover, we have
. Moreover, we have  [4]. Let
[4]. Let  . Let
. Let  be the root system of type
be the root system of type  :
: . Here the
. Here the  form the standard orthonormal basis of the Euclidean space
form the standard orthonormal basis of the Euclidean space  . Let ( , ) denote the inner product on this space and define simple roots
. Let ( , ) denote the inner product on this space and define simple roots  and positive roots
and positive roots  .
.
Theorem 1[10] The q-Schur algebras  are generated by the elements
are generated by the elements  ,
,  ,
,  , subject to the following relations:
, subject to the following relations:
 ;
;
Let  be the set of all
be the set of all  matrices over
matrices over 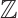 with all off-diagonal entries in
with all off-diagonal entries in  . Let
. Let  be the subset of
be the subset of  consisting of matrices with entries all in
consisting of matrices with entries all in  , and let
, and let  to be the map sending a matrix to the sum of its entries. Then, for
to be the map sending a matrix to the sum of its entries. Then, for  , the inverse image
, the inverse image  is the subset of
is the subset of  whose entries sum to
whose entries sum to  . For
. For  , let
, let  be the matrix
be the matrix  with
with  . Let
. Let  be the set of all
be the set of all  whose diagonal entries are zero. Let
whose diagonal entries are zero. Let  be the set of all
be the set of all  such that
such that  for all
for all  and
and  be the set of all
be the set of all  whose diagonal entries are zero. Let
whose diagonal entries are zero. Let  be the set of all
be the set of all  such that
such that  for
for  with
with  . Let
. Let  ,
,  .
.
Similar to monomial basis for q-Schur algebra  [10], we give the following definition. For
[10], we give the following definition. For  , put
, put
The orders in which the products  and
and  are taken are respectively defined as follows. Put
are taken are respectively defined as follows. Put
where 
Let  ,
,  ,
,  for
for  and
and  , then we have
, then we have
Proposition 1[9] 1) For any  , we have
, we have
and similar results for  can be obtained by applying the isomorphism
can be obtained by applying the isomorphism  .
.
2) Let  , then
, then  for
for  .
.
Theorem 2[9] The set  forms a basis for q-Schur algebra
forms a basis for q-Schur algebra  .
.
Let  , hence
, hence  naturally induces a surjective homomorphism
naturally induces a surjective homomorphism
When  is odd, since
is odd, since  ,
,  naturally induces a map from
naturally induces a map from  to
to 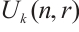 . We call the image
. We call the image  the little q-Schur algebra and denote it by
the little q-Schur algebra and denote it by  . When
. When  is even, by restriction, we also get a map
is even, by restriction, we also get a map  , then
, then  . By abuse of notations, we shall continue to denote the images of the generators
. By abuse of notations, we shall continue to denote the images of the generators  for
for  by the same letters
by the same letters  used for
used for  .
.
Let  (resp,
(resp, ,
, (resp,
(resp, ,
, (resp,
(resp, . For a positive integer
. For a positive integer  , let
, let  , set
, set
be the map defined by  .
.
Let  . For
. For  , define
, define
Proposition 2[10] For  ,
,
1) If there exist  for all
for all  and
and  , then
, then  where
where  otherwise,
otherwise,  .
.
2) If there exist  for all
for all  and
and  , then
, then  where
where  ; otherwise,
; otherwise,  .
.
2 The Little q-Schur Algebra 
Theorem 3 The set  forms a basis for
forms a basis for  .
.
Proof Fix  satisfying
satisfying  for all
for all  . By the definition of
. By the definition of  , we have
, we have
In the q-Schur algebra  , for any
, for any  , if
, if  for some
for some  , then it lies in the span of
, then it lies in the span of  in the Theorem 2. Then we have
in the Theorem 2. Then we have
By Theorem 2, the elements above are linearly independent, thus the set  is linearly independent.
is linearly independent.
Assume that  . Inspired by Ref.[17], we have the following commutation formulas in the q-Schur algebras
. Inspired by Ref.[17], we have the following commutation formulas in the q-Schur algebras  .
.
Lemma 1 In the little q-Schur algebra  , for
, for  ,
,  satisfying
satisfying  for
for  , we have
, we have  , where
, where  ,
,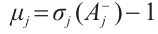 and
and  , if
, if  ;
;  , if
, if  .
.
Proof For  where
where  , and
, and  if
if  . We may assume
. We may assume  ,
,  for all
for all  . By the definition of
. By the definition of  and commutation formulas between positive root vectors, it is enough to show for all
and commutation formulas between positive root vectors, it is enough to show for all 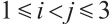 ,
,
Here, we no longer discuss the situations of  in 2) of Proposition 2 alone.We consider
in 2) of Proposition 2 alone.We consider  , where
, where  , then
, then
Case 1  . It is supposed that
. It is supposed that  , according to the commutation formula
, according to the commutation formula  , we get
, we get
Thus, there exist some  such that
such that  .
.
Case 1-1 If  , by Proposition 1(1), it follows
, by Proposition 1(1), it follows  ;
;
Case 1-2 If  , i.e.
, i.e.  , then we have
, then we have
By 2) of Proposition 1 and  , we also obtain
, we also obtain
When 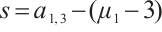 , we have
, we have  .
.
Case 2  , assuming
, assuming 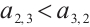 , by the commutation formulas
, by the commutation formulas  ,
,  and
and  , we have
, we have
Similarly, there exist some  such that
such that  .
.
Case 2-1 If  , by Proposition 1 1), it follows that
, by Proposition 1 1), it follows that  ;
;
Case 2-2 If  , namely
, namely  , then we have
, then we have
then
When 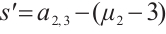 , we also find
, we also find  .
.
For  where
where  , the proof is similar to the above, thus we need not to give. Then we complete the proof of Lemma 1.
, the proof is similar to the above, thus we need not to give. Then we complete the proof of Lemma 1.
Theorem 4 The little q-Schur algebra  can be generated by the elements
can be generated by the elements  ,
,  subject to the following relations:
subject to the following relations:
 ;
;
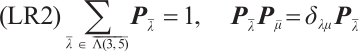 ;
;
 ;
;
 ;
;
 ;
;

 (resp.
(resp.  ) for
) for  (resp.
(resp.  ) and
) and  satisfies that if
satisfies that if  with
with  then
then  ;
;
 For
For  ,
, 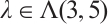 with
with  for
for  , then
, then  , where
, where  satisfies
satisfies  and
and  if
if  ,
,  if
if  .
.
We define an algebra  which satisfies the generators and relations given in Theorem 4. Set
which satisfies the generators and relations given in Theorem 4. Set  (resp.
(resp.  ,
, ) be the subalgebra generated by
) be the subalgebra generated by 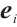 (resp.
(resp. 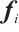 ,
, ). For
). For  , we give the root vectors, which satisfy the commutation formulas
, we give the root vectors, which satisfy the commutation formulas  in the same way. According to the relations (LR3)-(LR7) in Theorem 4, we know that
in the same way. According to the relations (LR3)-(LR7) in Theorem 4, we know that  can be spanned by all the elements
can be spanned by all the elements  ,
,  .
.
Proposition 3 The set 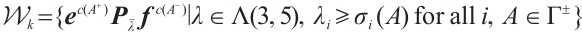 is a spanning set for
is a spanning set for  .
.
Proof Fixing  , to prove this proposition, it suffices to show that if
, to prove this proposition, it suffices to show that if  with
with  , satisfying
, satisfying  for some
for some  , then
, then  lies in the span of
lies in the span of  . Here
. Here  is a linear combination of the elements in
is a linear combination of the elements in  and
and  is a constant.
is a constant.
Case 1 If  and
and  , assuming
, assuming  , for
, for  , by the commutation formulas
, by the commutation formulas  -
- , we have
, we have
Therefore, we only need to consider  .
.
By Lemma 1, we have  when
when  , then we obtain that
, then we obtain that  is a linear combination of the elements in
is a linear combination of the elements in  .
.
Case 2 If  , there is an assumption that
, there is an assumption that  and
and  . Then, we only need to consider
. Then, we only need to consider  . By the commutation formulas
. By the commutation formulas  and
and  , we have
, we have
By Lemma 1, when  , we have
, we have  . Hence,
. Hence,
When 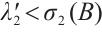 appears in
appears in  , we only require to exchange
, we only require to exchange  (resp.
(resp.  ) and other
) and other  (resp.
(resp.  ) into the Case 1 via commutation formulas. Finally, we give the proof of Theorem 4.
) into the Case 1 via commutation formulas. Finally, we give the proof of Theorem 4.
The proof of Theorem 4 By the definition of  and Theorem 1, it is clear that
and Theorem 1, it is clear that  satisfies the relations
satisfies the relations  . Hence, there is a surjective algebra homomorphism from
. Hence, there is a surjective algebra homomorphism from  to
to  . On the foundations of Proposition 1, Proposition 2 and Lemma 1, we have the
. On the foundations of Proposition 1, Proposition 2 and Lemma 1, we have the  that satisfies the relations in Theorem 4. And according to the definition of
that satisfies the relations in Theorem 4. And according to the definition of  , there is a surjective algebra homomorphism
, there is a surjective algebra homomorphism  from
from  to
to  satisfying
satisfying  ,
,  ,
,  . On the other hand, by Proposition 3, we see that the map
. On the other hand, by Proposition 3, we see that the map  sends the spanning set of
sends the spanning set of  to the basis of
to the basis of  . Hence
. Hence  is an isomorphism.
is an isomorphism.
Remark 1 For the presentation of little q-Schur algebra  in this paper, if we only consider
in this paper, if we only consider  for some j, then the relation (LR9) in Theorem 4 is more general than the relations
for some j, then the relation (LR9) in Theorem 4 is more general than the relations  ,
,  and
and  in Ref.[12,3]. As
in Ref.[12,3]. As  becomes increasingly great, we need to consider several
becomes increasingly great, we need to consider several  at the same time. Then there may be other more complex relations. For example, when
at the same time. Then there may be other more complex relations. For example, when  the relation
the relation  cannot be obtained by the relations (LR1)-(LR9). In conclusion, it is more difficult to study the generators and relations for
cannot be obtained by the relations (LR1)-(LR9). In conclusion, it is more difficult to study the generators and relations for  .
.
References
- Dipper R, James G. The q-Schur algebras[J]. Proceedings of the London Mathematical Society, 1989, 59(1): 23-50. [Google Scholar]
- Dipper R, James G. q-Tensor spaces and q-Weyl modules[J]. Transactions of the American Mathematical Society, 1991, 327(1): 251-282. [MathSciNet] [Google Scholar]
-
Beilinson A A, Lusztig G, Macpherson R. A geometric setting for the quantum deformation of
 [J]. Duke Mathematical Journal, 1990, 61(2): 655-677.
[CrossRef]
[MathSciNet]
[Google Scholar]
[J]. Duke Mathematical Journal, 1990, 61(2): 655-677.
[CrossRef]
[MathSciNet]
[Google Scholar]
- Du J E. A note on the quantized Weyl reciprocity at roots of unity[J]. Algebra Colloquium, 1995, 2(4): 363-372. [MathSciNet] [Google Scholar]
-
Du J E, Fu Q A, Wang J P. Infinitesimal quantum
 and little q-Schur algebras[J]. Journal of Algebra, 2005, 287(1): 199-233.
[CrossRef]
[MathSciNet]
[Google Scholar]
and little q-Schur algebras[J]. Journal of Algebra, 2005, 287(1): 199-233.
[CrossRef]
[MathSciNet]
[Google Scholar]
- Du J E, Fu Q A, Wang J P. Representations of little q-Schur algebras[J]. Pacific Journal of Mathematics, 2012, 257(2): 343-377. [CrossRef] [MathSciNet] [Google Scholar]
- Fu Q A. Little q-Schur algebras at even roots of unity[J]. Journal of Algebra, 2007, 311(1): 202-215. [CrossRef] [MathSciNet] [Google Scholar]
- Bian Z H, Liu M Q. Representation type of the little q-Schur algebras[J]. Journal of Pure and Applied Algebra, 2020, 224(8): 106349. [CrossRef] [MathSciNet] [Google Scholar]
- Doty S, Giaquinto A. Presenting Schur algebras[J]. International Mathematics Research Notices, 2002, 2002(36): 1907-1944. [CrossRef] [Google Scholar]
- Du J E, Parshall B. Monomial bases for q-Schur algebras[J]. Transactions of the American Mathematical Society, 2003, 355(4): 1593-1620. [MathSciNet] [Google Scholar]
-
Bian Z H, Liu M Q. Presenting little q-Schur algebras
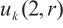 [J]. Algebra Colloquium, 2017, 24(2): 297-308.
[CrossRef]
[MathSciNet]
[Google Scholar]
[J]. Algebra Colloquium, 2017, 24(2): 297-308.
[CrossRef]
[MathSciNet]
[Google Scholar]
-
Gao W T, Liu M Q. The generators and relations for little q-Schur algebra
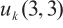 [J]. Acta Mathematica Scientia (Chinese Series), 2022, 65(5): 819-826(Ch).
[MathSciNet]
[Google Scholar]
[J]. Acta Mathematica Scientia (Chinese Series), 2022, 65(5): 819-826(Ch).
[MathSciNet]
[Google Scholar]
-
Takeuchi M. Some topics on
 [J]. Journal of Algebra, 1992, 147(2): 379-410.
[CrossRef]
[MathSciNet]
[Google Scholar]
[J]. Journal of Algebra, 1992, 147(2): 379-410.
[CrossRef]
[MathSciNet]
[Google Scholar]
-
Jimbo M. A q-analogue of
 , Hecke algebras, and the Yang-Baxter equation[J]. Letters in Mathematical Physics, 1986, 11(3): 247-252.
[NASA ADS]
[CrossRef]
[MathSciNet]
[Google Scholar]
, Hecke algebras, and the Yang-Baxter equation[J]. Letters in Mathematical Physics, 1986, 11(3): 247-252.
[NASA ADS]
[CrossRef]
[MathSciNet]
[Google Scholar]
- Lusztig G. Canonical bases arising from quantized enveloping algebras[J]. Journal of the American Mathematical Society, 1990, 3(2): 447-498. [CrossRef] [MathSciNet] [Google Scholar]
- Lusztig G. Finite dimensional Hopf algebras arising from quantized universal enveloping algebras[J]. Journal of the American Mathematical Society, 1990, 3(1): 257-296. [MathSciNet] [Google Scholar]
- Xi N H. Root vectors in quantum groups[J]. Commentarii Mathematici Helvetici, 1994, 69(1): 612-639. [CrossRef] [MathSciNet] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.