Open Access
| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 28, Number 5, October 2023
|
|
|---|---|---|
| Page(s) | 385 - 391 | |
| DOI | https://doi.org/10.1051/wujns/2023285385 | |
| Published online | 10 November 2023 | |
- Dipper R, James G. The q-Schur algebras[J]. Proceedings of the London Mathematical Society, 1989, 59(1): 23-50. [Google Scholar]
- Dipper R, James G. q-Tensor spaces and q-Weyl modules[J]. Transactions of the American Mathematical Society, 1991, 327(1): 251-282. [MathSciNet] [Google Scholar]
-
Beilinson A A, Lusztig G, Macpherson R. A geometric setting for the quantum deformation of
[J]. Duke Mathematical Journal, 1990, 61(2): 655-677.
[CrossRef]
[MathSciNet]
[Google Scholar]
- Du J E. A note on the quantized Weyl reciprocity at roots of unity[J]. Algebra Colloquium, 1995, 2(4): 363-372. [MathSciNet] [Google Scholar]
-
Du J E, Fu Q A, Wang J P. Infinitesimal quantum
and little q-Schur algebras[J]. Journal of Algebra, 2005, 287(1): 199-233.
[CrossRef]
[MathSciNet]
[Google Scholar]
- Du J E, Fu Q A, Wang J P. Representations of little q-Schur algebras[J]. Pacific Journal of Mathematics, 2012, 257(2): 343-377. [CrossRef] [MathSciNet] [Google Scholar]
- Fu Q A. Little q-Schur algebras at even roots of unity[J]. Journal of Algebra, 2007, 311(1): 202-215. [CrossRef] [MathSciNet] [Google Scholar]
- Bian Z H, Liu M Q. Representation type of the little q-Schur algebras[J]. Journal of Pure and Applied Algebra, 2020, 224(8): 106349. [CrossRef] [MathSciNet] [Google Scholar]
- Doty S, Giaquinto A. Presenting Schur algebras[J]. International Mathematics Research Notices, 2002, 2002(36): 1907-1944. [CrossRef] [Google Scholar]
- Du J E, Parshall B. Monomial bases for q-Schur algebras[J]. Transactions of the American Mathematical Society, 2003, 355(4): 1593-1620. [MathSciNet] [Google Scholar]
-
Bian Z H, Liu M Q. Presenting little q-Schur algebras
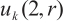[J]. Algebra Colloquium, 2017, 24(2): 297-308.
[CrossRef]
[MathSciNet]
[Google Scholar]
-
Gao W T, Liu M Q. The generators and relations for little q-Schur algebra
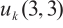[J]. Acta Mathematica Scientia (Chinese Series), 2022, 65(5): 819-826(Ch).
[MathSciNet]
[Google Scholar]
-
Takeuchi M. Some topics on
[J]. Journal of Algebra, 1992, 147(2): 379-410.
[CrossRef]
[MathSciNet]
[Google Scholar]
-
Jimbo M. A q-analogue of
, Hecke algebras, and the Yang-Baxter equation[J]. Letters in Mathematical Physics, 1986, 11(3): 247-252.
[NASA ADS]
[CrossRef]
[MathSciNet]
[Google Scholar]
- Lusztig G. Canonical bases arising from quantized enveloping algebras[J]. Journal of the American Mathematical Society, 1990, 3(2): 447-498. [CrossRef] [MathSciNet] [Google Scholar]
- Lusztig G. Finite dimensional Hopf algebras arising from quantized universal enveloping algebras[J]. Journal of the American Mathematical Society, 1990, 3(1): 257-296. [MathSciNet] [Google Scholar]
- Xi N H. Root vectors in quantum groups[J]. Commentarii Mathematici Helvetici, 1994, 69(1): 612-639. [CrossRef] [MathSciNet] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.