EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 30 / No 2 (April 2025) Wuhan Univ. J. Nat. Sci., 30 2 (2025) 159-168 References
Open Access
Issue
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 2, April 2025
Page(s) 159 - 168
DOI https://doi.org/10.1051/wujns/2025302159
Published online 16 May 2025
  1. Cottle R, Pang J S, Stone R E. The Linear Complementarity Problem[M]. Boston: Academic Press, 1992. [Google Scholar]
  2. Kojima M, Megiddo N, Noma T, Yoshise A. Progress in Mathematical Programming: A Primal-Dual Interior Point Algorithm for Linear Programming[M]. New York: Springer-Verlag, 1989. [Google Scholar]
  3. Wang G Q, Bai Y Q. A new primal-dual path-following interior-point algorithm for semidefinite optimization[J]. Journal of Mathematical Analysis and Applications, 2009, 353(1): 339-349. [Google Scholar]
  4. Wang G Q, Bai Y Q. A primal-dual interior-point algorithm for second-order cone optimization with full Nesterov-Todd step[J]. Applied Mathematics and Computation, 2009, 215(3): 1047-1061. [Google Scholar]
  5. Potra F A. A superlinearly convergent predictor-corrector method for degenerate LCP in a wide neighborhood of the central path with-iteration complexity[J]. Mathematical Programming, 2004, 100(2): 317-337. [Google Scholar]
  6. Kojima M, Megiddo N, Noma T, et al. A unified approach to interior point algorithms for linear complementarity problems: A summary[J]. Operations Research Letters, 1991, 10(5): 247-254. [Google Scholar]
  7. Illés T, Nagy M. A Mizuno-Todd-Ye type predictor-corrector algorithm for sufficient linear complementarity problems[J]. European Journal of Operational Research, 2007, 181(3): 1097-1111. [Google Scholar]
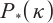  8. Wang G Q, Yu C J, Teo K L. A full-Newton step feasible interior-point algorithm for Formula -linear complementarity problem[J]. Global Optimization, 2014, 59: 81-99. [Google Scholar]
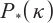  9. Zhang M W, Huang K, Li M M, et al. A new full-Newton step interior-point method for Formula -LCP based on a positive-asymptotic kernel function[J]. Journal of Applied Mathematics and Computation, 2020, 64: 313-330. [Google Scholar]
  10. Geng J, Zhang M W, Zhu D C. A full-Newton step feasible interior-point algorithm for the special weighted linear complementarity problems based on a kernel function[J]. Wuhan Univ J of Nat Sci, 2024, 29(1): 29-37. [Google Scholar]
  11. Geng J, Zhang M W, Pang J J. A full-Newton step feasible IPM for semidefinite optimization based on a kernel function with linear growth term[J]. Wuhan Univ J of Nat Sci, 2020, 25(6): 501-509. [Google Scholar]
  12. Yang Y G. A polynomial arc-search interior-point algorithm for linear programming[J]. Journal of Optimization Theory and Applications, 2013, 158(3): 859-873. [Google Scholar]
  13. Shahraki M S, Delavarkhalafi A. An arc-search predictor-corrector infeasible-interior-point algorithm for P(κ)-SCLCPs[J]. Numerical Algorithms, 2020, 83(4): 1555-1575. [Google Scholar]
  14. Yang Y G. Arc-Search Techniques for Interior-Point Methods[M]. Boca Raton: CRC press, 2020. [CrossRef] [Google Scholar]
  15. Yuan B B, Zhang M W, Huang Z G. A wide neighborhood arc-search interior-point algorithm for convex quadratic programming[J]. Wuhan Univ J of Nat Sci, 2017, 22(6): 465-471. [Google Scholar]
  16. Darvay Z. New interior-point algorithms in linear programming[J]. Advanced Modeling and Optimization, 2003, 5(1):51-92. [Google Scholar]
  17. Achache M. A new primal-dual path-following method for convex quadratic programming[J]. Computational & Applied Mathematics, 2006, 25(1): 97-110. [Google Scholar]
  18. Wang G Q, Lesaja G. Full Nesterov-Todd step feasible interior-point method for the Cartesian P*(κ)-SCLCP[J]. Optimization Methods and Software, 2013, 28(3): 600-618. [Google Scholar]
  19. Mansouri H, Pirhaji M. A polynomial interior-point algorithm for monotone linear complementarity problems[J]. Journal of Optimization Theory and Applications, 2013, 157(2): 451-461. [Google Scholar]
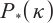  20. Asadi S, Mansouri H. Polynomial interior-point algorithm for Formula horizontal linear complementarity problems[J]. Numerical Algorithms, 2013, 63: 385-398. [Google Scholar]
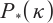  21. Illés T, Rigó P R, Török R. Unified approach of interior-point algorithms for Formula -LCP using a new class of algebraically equivalent transformations[J]. Optimization Theory and Applications, 2023, 202: 27-49. [Google Scholar]
  22. Kheirfam B, Nasrollahi A. A full-Newton step interior-point method based on a class of specific algebra transformation[J]. Fundamenta Informaticae, 2018, 163(4): 325-337. [Google Scholar]
  23. Grimes W, Achache M. A path-following interior-point algorithm for monotone LCP based on a modified Newton search direction[J]. RAIRO-Operations Research, 2023, 57(3): 1059-1073. [Google Scholar]
  24. Darvay Z, Papp I M, Takács P R. Complexity analysis of a full-Newton step interior-point method for linear optimization[J]. Periodica Mathematica Hungarica, 2016, 73(1): 27-42. [Google Scholar]
  25. Darvay Z, Illés T, Majoros C. Interior-point algorithm for sufficient LCPs based on the technique of algebraically equivalent transformation[J]. Optimization Letters, 2021, 15(2): 357-376. [Google Scholar]
  26. Illés T, Nagy M, Terlaky T. A polynomial path-following interior point algorithm for general linear complementarity problems[J]. Journal of Global Optimization, 2010, 47(3): 329-342. [Google Scholar]
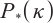  27. Lee Y H, Cho Y Y, Cho G M. Interior-point algorithms for Formula -LCP based on a new class of kernel functions[J]. Journal of Global Optimization, 2014, 58(1): 137-149. [Google Scholar]
  28. Harker Patrick T, Pang J S. A damped-Newton method for the linear complementarity problem[J]. Lectures in Applied Mathematics, 1990, 26: 265-284. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.