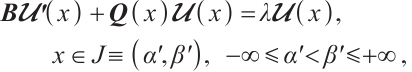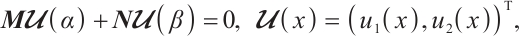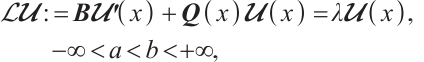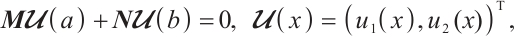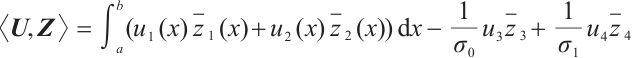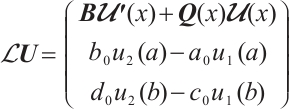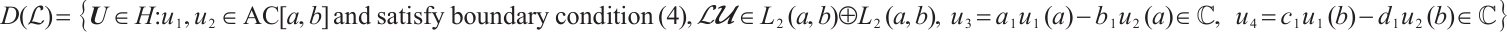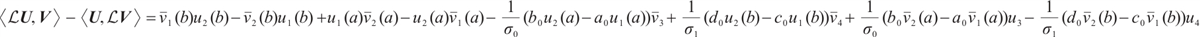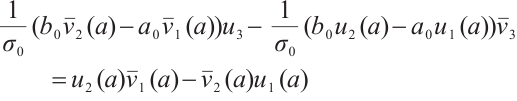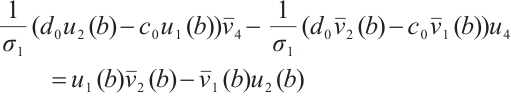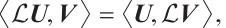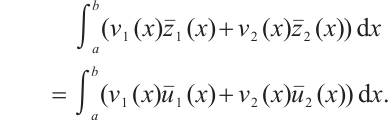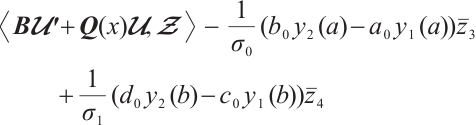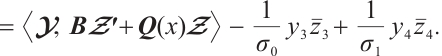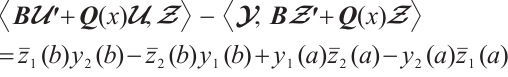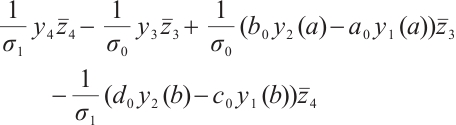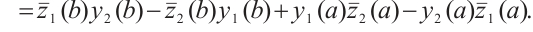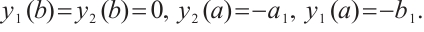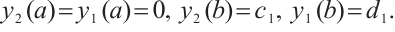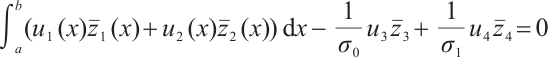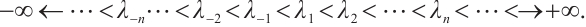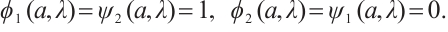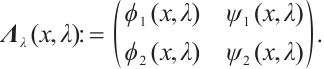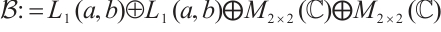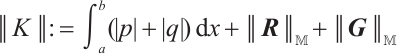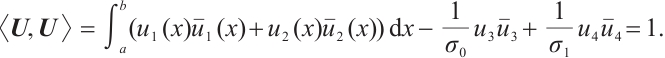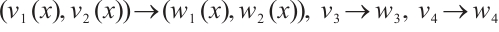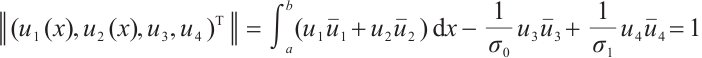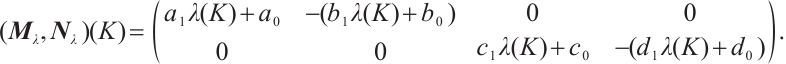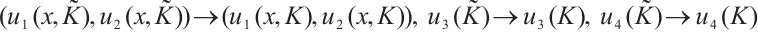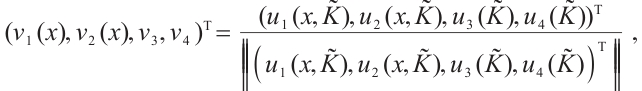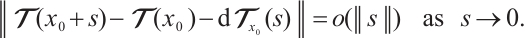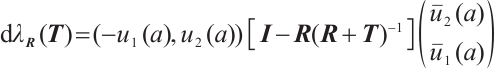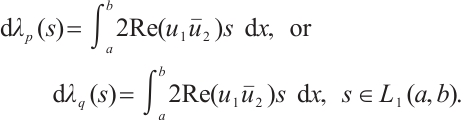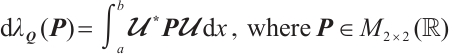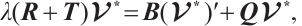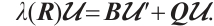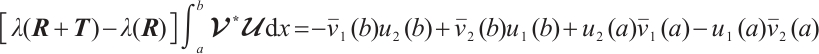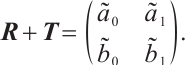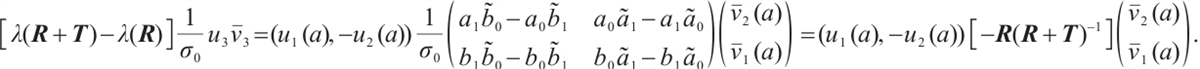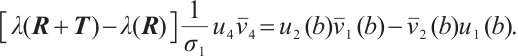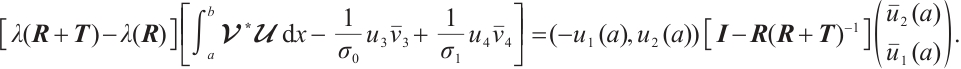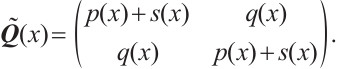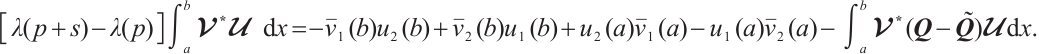| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
|
|
|---|---|---|
| Page(s) | 263 - 268 | |
| DOI | https://doi.org/10.1051/wujns/2025303263 | |
| Published online | 16 July 2025 | |
Mathematics
CLC number: O175.9
Spectral Properties of Dirac Operator with λ-Dependent Boundary Condition
边界条件含有谱参数的Dirac算子的谱性质
College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, Gansu, China
† Corresponding author. E-mail: dgf96520@163.com
Received:
28
November
2024
In this study, we mainly discuss some spectral properties of the Dirac operator with eigenparameter-dependent boundary condition. Initially, we reformulate the spectral problem into linear operator eigenparameter problem in a suitable Hilbert space, and obtain some pivotal properties of self-adjoint operator. Subsequently, by establishing the boundary condition space and constructing the embedded mapping, we show that the simple eigenvalue branch of this system is not only continuous, but also smooth. We then obtain the differential expressions of the eigenvalue branch in the sense of Fréchet derivative.
摘要
本文主要研究边界条件含有谱参数的Dirac算子特征值问题的一些谱性质。首先,通过建立适当的Hilbert空间将谱问题转化为线性算子特征值问题,并推导出了自伴算子的一些重要性质。其次,通过建立边界条件空间,构造嵌入映射,证明了Dirac算子的简单特征值分支不仅是连续的,而且是光滑的。最后,在Fréchet导数意义下,我们得到了特征值分支关于所有参数的微分表达式。
Key words: λ-dependent boundary condition / spectral properties / Dirac operator
关键字 : 特征参数依赖边界条件 / 谱性质 / Dirac算子
Cite this article: ZHONG Linlu, DU Gaofeng. Spectral Properties of Dirac Operator with λ-Dependent Boundary Condition[J]. Wuhan Univ J of Nat Sci, 2025, 30(3): 263-268.
Biography: ZHONG Linlu, female, Master candidate, research direction: ordinary differential equations and dynamic systems. E-mail: rqzhong0510@163.com
Foundation item: Supported by the National Natural Science Foundation of China (12461039) and Excellent Graduate Innovation Star Scientific Research Project of Gansu Province of China (2025CXZX-273)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Dirac operators are important models in quantum mechanics. As a result, some conclusions about these operators have been obtained (see Refs. [1-4]). As a typical problem in the spectral theory of differential operators, Dirac operators are closely related to Sturm-Liouville operators, and they have many similarities in the properties and research methods of eigenvalues, see Refs. [5-9]. In particular, in Ref. [10], Li et al studied the continuous dependence of eigenvalue of self-adjoint Dirac system consisting of the symmetric differential operator
where 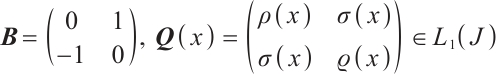 and
and 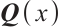 is real-valued Lebesgue measurable function on
is real-valued Lebesgue measurable function on 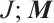 and
and 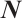 are
are  complex matrices such that rank
complex matrices such that rank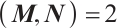 and satisfy
and satisfy 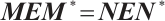 , where
, where  denotes the complex conjugate transpose of
denotes the complex conjugate transpose of 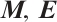 is the second order symplectic matrix. Besides, we are also interested in the spectral analysis of Dirac operator with the spectral parameter in boundary condition, which has a discrete spectrum consisting of an increasing infinite sequence of (real, simple) eigenvalues
is the second order symplectic matrix. Besides, we are also interested in the spectral analysis of Dirac operator with the spectral parameter in boundary condition, which has a discrete spectrum consisting of an increasing infinite sequence of (real, simple) eigenvalues 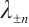 such that
such that 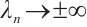 as
as 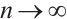 , see Ref. [11], and some remarkable works have been reached, see Refs. [12-13].
, see Ref. [11], and some remarkable works have been reached, see Refs. [12-13].
From the above literature, we notice that the research on problems (1)-(2) requires that the boundary conditions satisfy 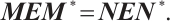 Typically, the eigenparameter is only present in differential equations. Nonetheless, in numerous practical applications, including mechanics and acoustic scattering theory, it is necessary for the spectral parameter to be featured not only within the differential equations but also within the boundary conditions, see Ref. [14]. Recently, inverse spectral problems for Sturm-Liouville operators with non-self-adjoint eigenparameter-dependent boundary conditions have been studied via matrix representations and inverse matrix eigenvalue problems, see Ref. [15]. For the above model the condition
Typically, the eigenparameter is only present in differential equations. Nonetheless, in numerous practical applications, including mechanics and acoustic scattering theory, it is necessary for the spectral parameter to be featured not only within the differential equations but also within the boundary conditions, see Ref. [14]. Recently, inverse spectral problems for Sturm-Liouville operators with non-self-adjoint eigenparameter-dependent boundary conditions have been studied via matrix representations and inverse matrix eigenvalue problems, see Ref. [15]. For the above model the condition 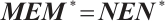 may not be satisfied. Therefore, we hope to get the correlation spectrum properties of this kind of problems. For example, considering the self-adjointness of operators and the continuous dependence of eigenvalues, it is necessary to discuss the eigenvalue problem of a linear operator in a suitable Hilbert space. To address the limitation that these boundary conditions lack self-adjointness, we construct a suitable Banach space and an embedded mapping, and prove the continuity of the embedded mapping. Moreover, based on the definition of Fréchet derivative, we obtain the differentiability of eigenvalue bifurcation.
may not be satisfied. Therefore, we hope to get the correlation spectrum properties of this kind of problems. For example, considering the self-adjointness of operators and the continuous dependence of eigenvalues, it is necessary to discuss the eigenvalue problem of a linear operator in a suitable Hilbert space. To address the limitation that these boundary conditions lack self-adjointness, we construct a suitable Banach space and an embedded mapping, and prove the continuity of the embedded mapping. Moreover, based on the definition of Fréchet derivative, we obtain the differentiability of eigenvalue bifurcation.
Our research plan is structured as follows. In Section 1, we introduce a self-adjoint operator eigenvalue problem and elucidate its critical spectral properties from various perspectives. In Section 2 and 3, leveraging the established continuity of the embedded mapping, we demonstrate the differentiability of the eigenvalue branch and present the corresponding derivative formulas.
1 Some Properties
This paper concerns eigenvalue problem of the form
where 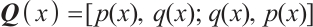 and every element in
and every element in 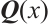 belongs to
belongs to 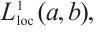
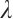 is the spectral parameter. Here, we require
is the spectral parameter. Here, we require 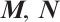 to satisfy
to satisfy 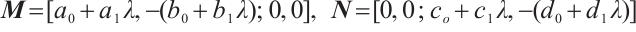 and
and 
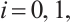 are real numbers satisfying
are real numbers satisfying 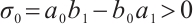 and
and 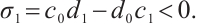
We first consider a linear operator eigenvalue problem derived from spectral problems (3)-(4). The inner product in the Hilbert space 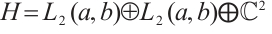 associated with
associated with
for 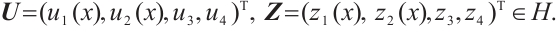 Define the operator
Define the operator 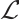 acting in
acting in 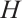 so that
so that
with the domain
Here 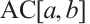 denotes the set of absolutely continuous and complex-valued functions on
denotes the set of absolutely continuous and complex-valued functions on 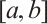 .
.
By immediate verification, we conclude that the problems (3)-(4) are equivalent to linear operator eigenvalue problem 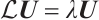 . We now focus on discussing the properties of linear operator
. We now focus on discussing the properties of linear operator 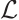 as follows.
as follows.
Theorem 1
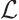 is a self-adjoint operator in
is a self-adjoint operator in 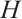 .
.
Proof In order to prove that the operator 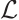 is self-adjoint, we first need to prove that the domain of operator
is self-adjoint, we first need to prove that the domain of operator 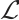 is dense in
is dense in 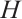 . Suppose
. Suppose 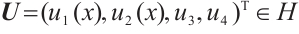 and
and 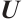 is orthogonal to
is orthogonal to 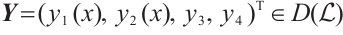 . We will prove
. We will prove  . Since
. Since 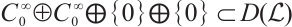 , for arbitrary
, for arbitrary 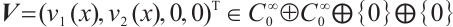 , we have
, we have 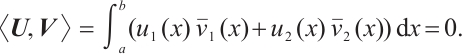 Since
Since 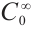 is dense in
is dense in 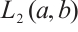 , we have
, we have 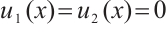 , so
, so 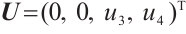 . For any
. For any  , through the inner product in
, through the inner product in 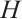 , we get
, we get 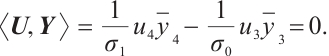 Since
Since 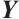 is arbitrary, we have
is arbitrary, we have 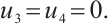 Hence
Hence 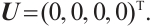
Secondly, we need to show that the operator 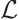 is symmetric. Let
is symmetric. Let 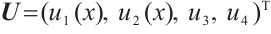 . For any
. For any 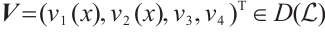 , then
, then
By the boundary condition (4), we have
Consequently, combining (5)-(7), we obtain
which implies that operator 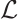 is symmetric.
is symmetric.
Since 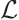 is symmetric, it suffices to prove that for any
is symmetric, it suffices to prove that for any 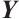 and some
and some 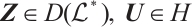 satisfying
satisfying 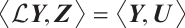 , then
, then 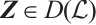 and
and 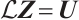 , where
, where 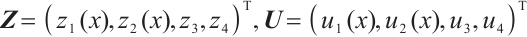 . It means that
. It means that  satisfies following conditions:
satisfies following conditions:
(ⅰ) 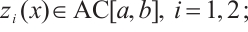
(ⅱ) 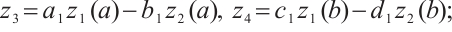
(ⅲ) 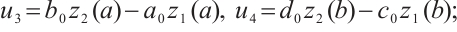
(ⅳ) 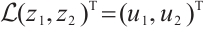 .
.
Indeed, the above conditions imply that 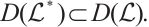
Step 1 For arbitrary 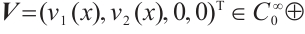
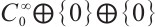 , there is
, there is 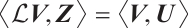 . Moreover, we arrive at
. Moreover, we arrive at
Namely, 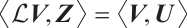 . Since
. Since 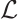 is symmetric, combined with
is symmetric, combined with 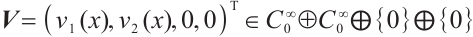 , we can obtain
, we can obtain 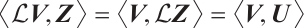 . In view of the classical theory of differential operators, (ⅰ) and (ⅳ) hold.
. In view of the classical theory of differential operators, (ⅰ) and (ⅳ) hold.
Step 2 According (ⅳ) and the relation 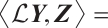
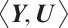 , we have
, we have
In light of
Furthermore, one has
Using Naimark’s patching lemma[16], there exists a 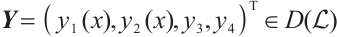 such that
such that
Then by (8), we have 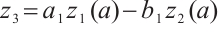 . Similarly, we get
. Similarly, we get
Moreover, 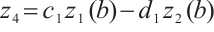 . Therefore, (ⅱ) holds. We can prove (ⅲ) by using the similar method, hence we omit the details. The proof is completed.
. Therefore, (ⅱ) holds. We can prove (ⅲ) by using the similar method, hence we omit the details. The proof is completed.
Corollary 1 The following assertions are true:
1) The two vector eigenfunctions corresponding to different eigenvalues of 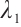 and
and 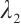 are orthogonal in the following sense
are orthogonal in the following sense
2) All eigenvalues of the operator 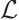 are real, and all vector-eigenfunctions are real-valued.
are real, and all vector-eigenfunctions are real-valued.
Theorem 2[11] There exists an unboundedly decreasing sequence 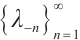 of negative eigenvalues and an unboundedly increasing sequence
of negative eigenvalues and an unboundedly increasing sequence 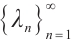 of nonnegative eigenvalues of the boundary value problems (3)-(4):
of nonnegative eigenvalues of the boundary value problems (3)-(4):
Let 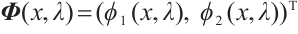 and
and 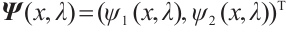 be the fundamental solutions of (3), which satisfy the initial condition
be the fundamental solutions of (3), which satisfy the initial condition
Then, 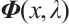 and
and 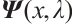 are linearly independent and entire functions of
are linearly independent and entire functions of 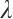 .
.
Denote
Lemma 1
 is an eigenvalue of (3)-(4) if and only if
is an eigenvalue of (3)-(4) if and only if 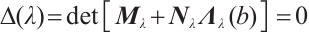 .
.
Proof By using similar methods in Ref. [10], we can obtain the assertion holds.
2 Continuous Dependence of Eigenvalues and Eigenfunction
Denote 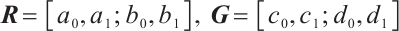 . We introduce Banach space
. We introduce Banach space
equipped with the norm
For any 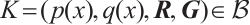 , where
, where 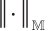 denotes the matrix normal. Let’s construct a boundary condition space
denotes the matrix normal. Let’s construct a boundary condition space 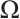 ={
={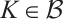 : the coefficient in (3)-(4), and
: the coefficient in (3)-(4), and 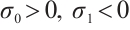 hold}. Then
hold}. Then 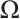 is a closed subset of
is a closed subset of 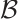 and inherits its topology
and inherits its topology 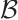 .
.
Theorem 3 Let 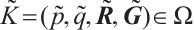 , and
, and 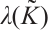 be an eigenvalue of spectral problems (3)-(4). Then for any sufficiently small
be an eigenvalue of spectral problems (3)-(4). Then for any sufficiently small 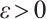 , there exists
, there exists 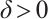 such that if
such that if 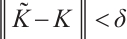 , the spectral problems (3)-(4) have exactly one eigenvalue satisfying
, the spectral problems (3)-(4) have exactly one eigenvalue satisfying 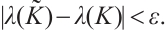
Proof It is well known that  is eigenvalue of (3)-(4) if and only if Lemma 1 holds. It is obvious that
is eigenvalue of (3)-(4) if and only if Lemma 1 holds. It is obvious that 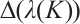 is not constant with regard to λ since λ is isolated eigenvalue. Furthermore, for any
is not constant with regard to λ since λ is isolated eigenvalue. Furthermore, for any 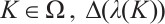 is an entire function of
is an entire function of 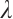 . Hence, there exists
. Hence, there exists 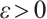 such that
such that 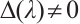 for
for 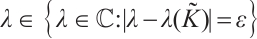 . By the well known theorem on continuity of the roots of an equation as a function of parameters, see Ref. [17], the assertion holds.
. By the well known theorem on continuity of the roots of an equation as a function of parameters, see Ref. [17], the assertion holds.
The normalized eigenfunction 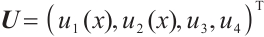 of spectral problems (3)-(4) is defined as follows:
of spectral problems (3)-(4) is defined as follows:
Theorem 4 Let 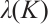 is an eigenvalue of operator
is an eigenvalue of operator 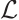 with
with 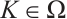 and
and 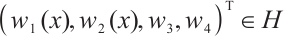 is a normalized eigenvector for
is a normalized eigenvector for 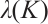 . Then there exists a normalized eigenvector
. Then there exists a normalized eigenvector 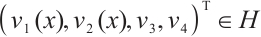 for
for 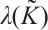 with
with 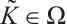 such that
such that
as 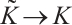 both uniformly on
both uniformly on 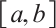 .
.
Proof We know that 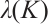 is simple. Let
is simple. Let 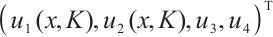 be a normalized eigenvector of operator
be a normalized eigenvector of operator 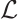 . Then in view of inner product in the Hilbert space H, we have
. Then in view of inner product in the Hilbert space H, we have
and 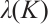 is the corresponding eigenvalue. Theorem 3 means that there exists
is the corresponding eigenvalue. Theorem 3 means that there exists 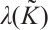 such that
such that 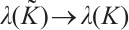 as
as 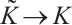 .
.
Denote the boundary conditions matrix as follows
Then 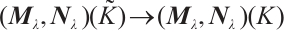 as
as 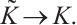 Besides, there exists
Besides, there exists 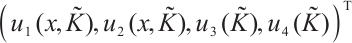 satisfying the
satisfying the 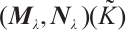 for
for 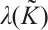 and
and 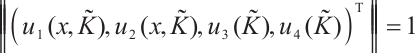 . Therefore, we obtain
. Therefore, we obtain
as 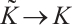 both uniformly on
both uniformly on 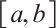 . Let
. Let
Then the desired assertion holds. The proof is completed.
3 Differentiability of Eigenvalue
In this section, we will prove that the simple eigenvalue branch is differentiable for all parameters and obtain the differential expression for all parameter in the sense of Fréchet derivative.
Definition 1[17] A map  from an open set
from an open set 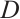 of the Banach space
of the Banach space  into the Banach space
into the Banach space 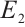 is Fréchet differentiable at a point
is Fréchet differentiable at a point 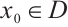 if there exists a bounded linear operator
if there exists a bounded linear operator 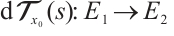 such that in some neighborhood of the
such that in some neighborhood of the 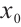 ,
,
Theorem 5 Let 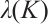 be an eigenvalue for the operator
be an eigenvalue for the operator 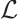 for
for 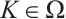 and
and 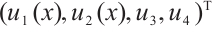 be a normalized eigenvector of
be a normalized eigenvector of 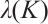 . Then
. Then 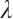 is Fréchet differentiable with respect to all parameters in
is Fréchet differentiable with respect to all parameters in 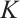 . Specifically, the derivative formulas of
. Specifically, the derivative formulas of 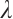 are given as follows:
are given as follows:
Result 1 Fix all components of 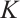 except the boundary matrix
except the boundary matrix 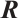 and let
and let 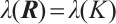 denote the eigenvalue. Then
denote the eigenvalue. Then
for all 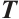 , where
, where 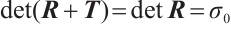 .
.
Result 2 Fix all components of 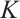 except the boundary matrix
except the boundary matrix 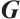 and let
and let 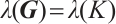 denote the eigenvalue. Then
denote the eigenvalue. Then 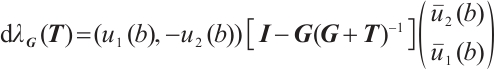 , for all
, for all 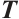 , where
, where 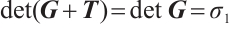 .
.
Result 3 Fix all components of 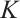 except
except 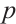 or
or 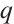 and let
and let 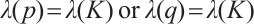 denote the eigenvalue. Then
denote the eigenvalue. Then
Result 4 Fix all components of 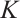 except
except 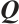 , and let
, and let 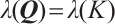 denote the eigenvalue. Then
denote the eigenvalue. Then
such that 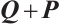 is symmetric and every element in
is symmetric and every element in 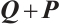 belong to
belong to 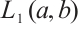 .
.
Proof 1) Let  denote the eigenvalue and corresponding normalize eigenvector. Direct computation yields
denote the eigenvalue and corresponding normalize eigenvector. Direct computation yields
By (9)-(10) and integration by parts, we obtain
Let
By (4), we have
Using the similar method, we can obtain
Combining (11)-(13), we have
Let 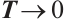 , then the desired Result 1 can be obtained by Theorem 4.
, then the desired Result 1 can be obtained by Theorem 4.
2) Using the similar method, we can obtain Result 2.
3) Fix all components of 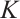 except
except 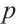 (the situation for
(the situation for 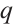 is similar). For
is similar). For 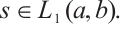
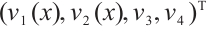 denote eigenvalue and corresponding normalized eigenvector. Let
denote eigenvalue and corresponding normalized eigenvector. Let
By (9) and (10), we have
By (4), we obtain 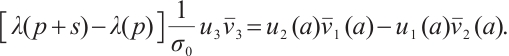
Similarly, 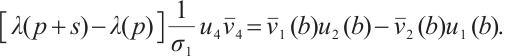
Hence
Then the desired Result 3 can be obtained.
4) In the same way, we can obtain Result 4. The proof is completed.
References
- Lott J. Eigenvalue bounds for the Dirac operator[J]. Pacific Journal of Mathematics, 1986, 125(1): 117-126. [Google Scholar]
- Levitan B M, Sargsjan I S. Sturm-Liouville and Dirac Operators[M]. Dordrecht: Kluwer Academic Publishers Group, 1991. [Google Scholar]
- Lunyov A A, Malamud M M. Stability of spectral characteristics of boundary value problems for 2×2 Dirac type systems. Applications to the damped string[J]. Journal of Differential Equations, 2022, 313: 633-742. [Google Scholar]
- Kh Amirov R, Keskin B, Ozkan A S. Direct and inverse problems for the Dirac operator with a spectral parameter linearly contained in a boundary condition[J]. Ukrainian Mathematical Journal, 2009, 61(9): 1365-1379. [Google Scholar]
- Du G F, Gao C H, Wang J J. Spectral analysis of discontinuous Sturm-Liouville operators with Herglotzs transmission[J]. Electronic Research Archive, 2023, 31(4): 2108-2119. [Google Scholar]
- Zhang M Z, Li K, Ju P J. Discontinuity of the nth eigenvalue for a vibrating beam equation[J]. Applied Mathematics Letters, 2024, 156: 109146. [Google Scholar]
- Lv X X, Ao J J, Zettl A. Dependence of eigenvalues of fourth-order differential equations with discontinuous boundary conditions on the problem[J]. Journal of Mathematical Analysis and Applications, 2017, 456(1): 671-685. [Google Scholar]
- Ao J J, Zhang L. An inverse spectral problem of Sturm-Liouville problems with transmission conditions[J]. Mediterranean Journal of Mathematics, 2020, 17(5):1-24. [Google Scholar]
- Zhang M Z, Li K. Dependence of eigenvalues of Sturm-Liouville problems with eigenparameter dependent boundary conditions[J]. Applied Mathematics and Computation, 2020, 378: 125214. [Google Scholar]
- Li K, Zhang M Z, Zheng Z W. Dependence of eigenvalues of Dirac system on the parameters[J]. Studies in Applied Mathematics, 2023, 150(4): 1201-1216. [Google Scholar]
- Kerimov N B. A boundary value problem for the Dirac system with a spectral parameter in the boundary conditions[J]. Differential Equations, 2002, 38(2): 164-174. [Google Scholar]
- Allahverdiev B P. A nonself-adjoint 1D singular Hamiltonian system with an eigenparameter in the boundary condition[J]. Potential Analysis, 2013, 38(4): 1031-1045. [Google Scholar]
- Allahverdiev B P. Extensions, dilations and functional models of Dirac operators[J]. Integral Equations and Operator Theory, 2005, 51(4): 459-475. [Google Scholar]
- Binding P A, Browne P J, Watson B A. Equivalence of inverse Sturm-Liouville problems with boundary conditions rationally dependent on the eigenparameter[J]. Journal of Mathematical Analysis and Applications, 2004, 291(1): 246-261. [Google Scholar]
- Zhang L, Ao J J, Lü W Y. Inverse Sturm-Liouville problems with a class of non-self-adjoint boundary conditions containing the spectral parameter[J]. Wuhan University Journal of Natural Sciences, 2024, 29(6): 508-516. [Google Scholar]
- Naimark M A. Linear Differential Operator[M]. New York: Frederick Ungar Publishing Company, 1968. [Google Scholar]
- Zettl A. Sturm-Liouville Theory[M]. Providence RI: American Mathematical Society, 2005. [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.