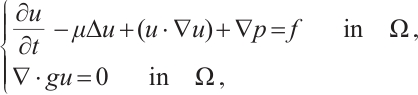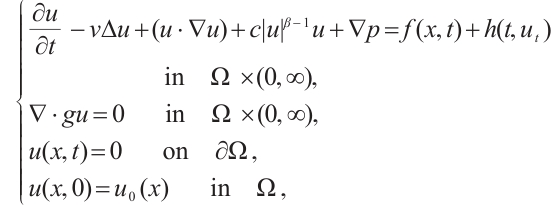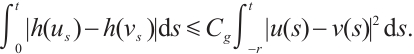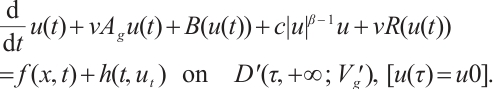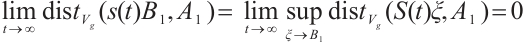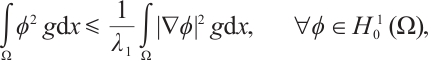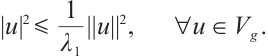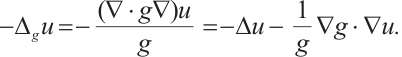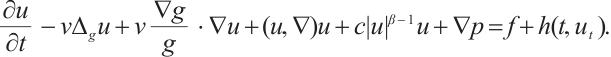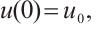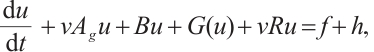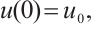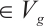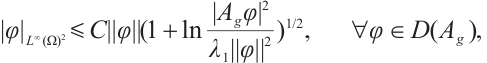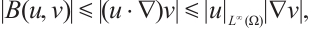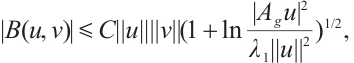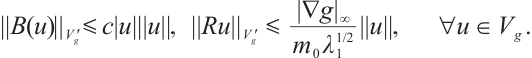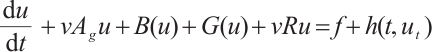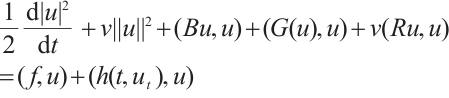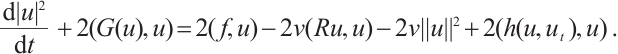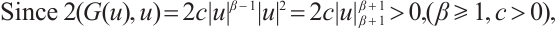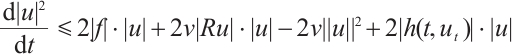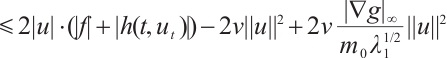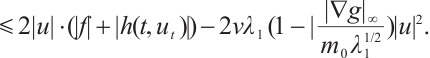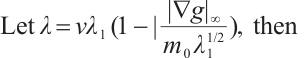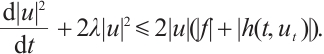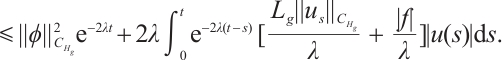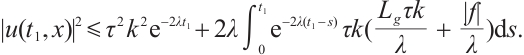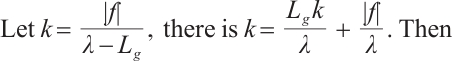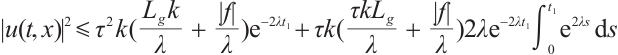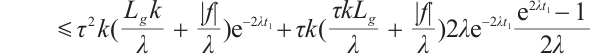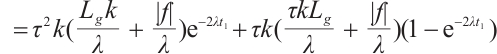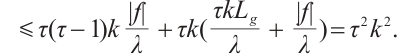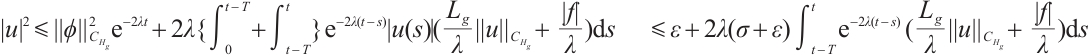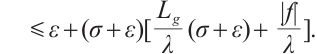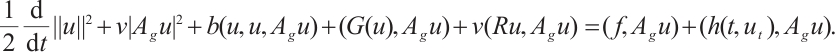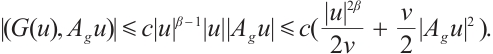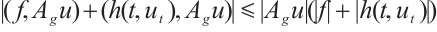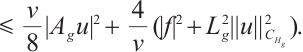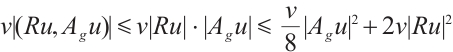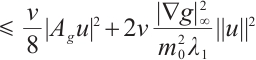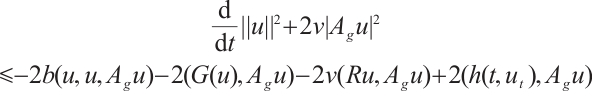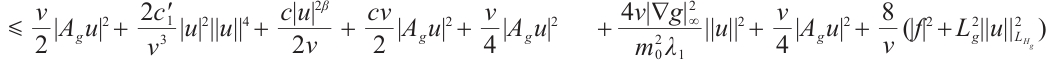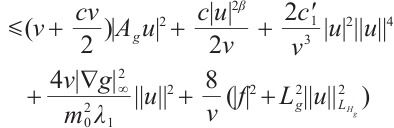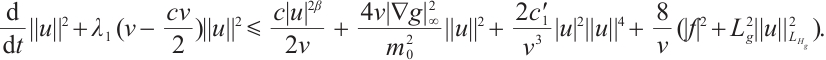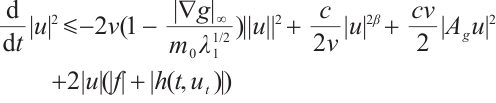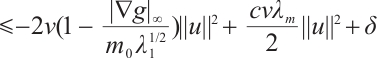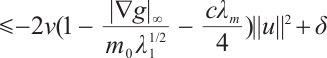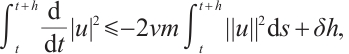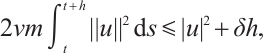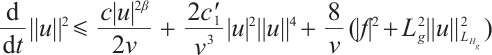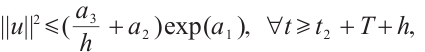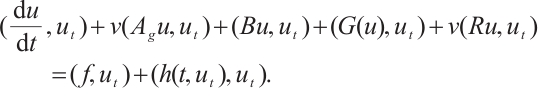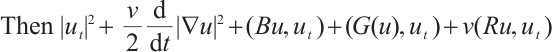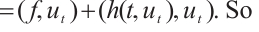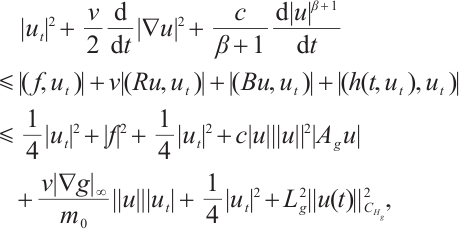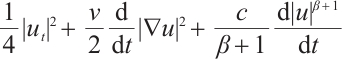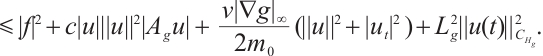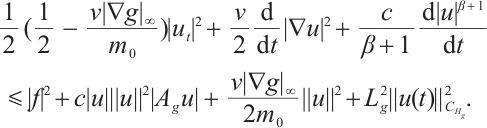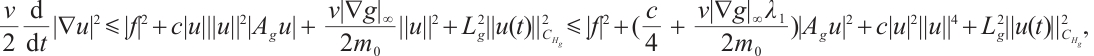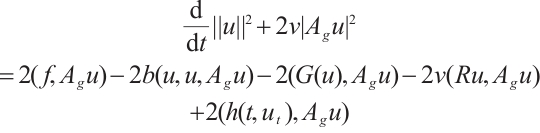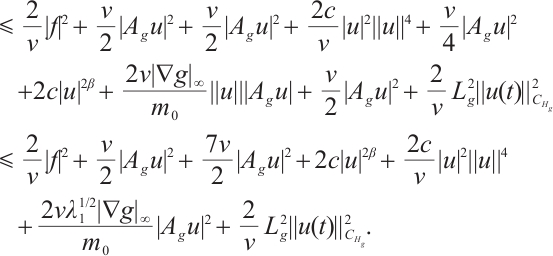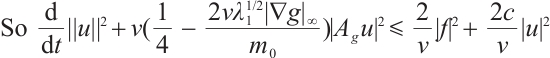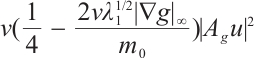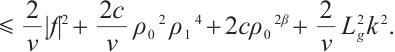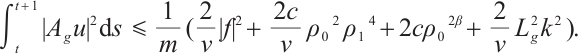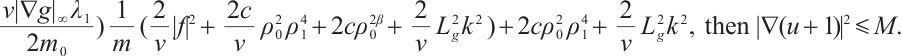| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
|
|
|---|---|---|
| Page(s) | 269 - 275 | |
| DOI | https://doi.org/10.1051/wujns/2025303269 | |
| Published online | 16 July 2025 | |
Mathematics
CLC number: O175
The Global Attractor of 2D g-Navier-Stokes Equations with Damping and Delay
含阻尼和时滞项的二维g-Navier-Stokes方程的全局吸引子
College of Mathematics and Computer Science, Yan′an University, Yan′an 716000, Shaanxi, China
Received:
5
September
2024
In this article, the global attractors of 2D g-Navier-Stokes equations are obtained in the space of 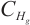 and
and 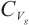 respectively. When the external force
respectively. When the external force 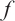 is sufficiently small, the studies indicate that the global attractor in
is sufficiently small, the studies indicate that the global attractor in 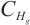 is equal to the global attractor in
is equal to the global attractor in 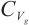 .
.
摘要
本文在空间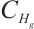 和空间
和空间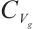 上分别得到了二维g-Navier-Stokes 方程的全局吸引子。研究结果表明,当外力项
上分别得到了二维g-Navier-Stokes 方程的全局吸引子。研究结果表明,当外力项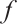 充分小时,在
充分小时,在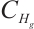 和
和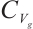 上得到的全局吸引子是相等的。
上得到的全局吸引子是相等的。
Key words: global attractor / g-Navier-Stokes equation / damping / delay
关键字 : 全局吸引子 / g-Navier-Stokes方程 / 阻尼 / 时滞
Cite this article: WANG Xiaoxia, JIANG Jinping, ZHANG Fukun. The Global Attractor of 2D g-Navier-Stokes Equations with Damping and Delay[J]. Wuhan Univ J of Nat Sci, 2025, 30(3): 269-275.
Biography: WANG Xiaoxia, female, Professor, research direction: nonlinear development equations and infinite-dimensional dynamical systems. E-mail: yd-wxx@163.com
Foundation item: Supported by the National Natural Science Foundation of China (11971378), Shaanxi Fundamental Science Research Project for Mathematics and Physics (23JSY050) and Shaanxi Innovative Training Program for College Students (S202410719114)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
The Navier-Stokes equations (NSE) are important in fluid mechanics and turbulence. In the last decades, the research on the asymptotic properties of the solution for NSE has attracted the attention of many scholars[1-7]. Especially in the past years, the NSE with nonlinear damping and delay has been studied[8-16], where the damping comes from the resistance of the flow or the friction effect. The delays denote some type of external forces that can be applied to control one system, and these forces can be regarded as the present state of the system or its history.
In recent years, the research on 2D g-Navier-Stokes equations (gNSE) has been paid more attention by scholars. It is derived from 3D NSE by the vertical mean operator in Ref. [17], and its form is as follows:
where 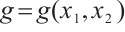 is a suitable smooth real-valued function defined on
is a suitable smooth real-valued function defined on 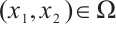 and
and 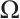 is the bounded domain in
is the bounded domain in 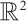 . We study the 2D gNSE as a small perturbation of the usual NSE, so we want to understand the NSE completely by studying the 2D gNSE systematically. Therefore, the research on the gNSE has a theoretical basis and practical significance.
. We study the 2D gNSE as a small perturbation of the usual NSE, so we want to understand the NSE completely by studying the 2D gNSE systematically. Therefore, the research on the gNSE has a theoretical basis and practical significance.
There are many researches on g-Navier-Stokes equations recently[18-26]. In Ref. [18], the well-posedness of solutions for gNSE was proved on  for
for 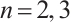 . In Ref. [19], Roh obtained the existence of the global attractors of gNSE and proved that the semiflows were robust to g. Moreover, the existence of global solutions and the global attractor of gNSE were proved, and the dimension of the global attractor was estimated in Ref. [20]. Also, the global attractor of gNSE with linear dampness on
. In Ref. [19], Roh obtained the existence of the global attractors of gNSE and proved that the semiflows were robust to g. Moreover, the existence of global solutions and the global attractor of gNSE were proved, and the dimension of the global attractor was estimated in Ref. [20]. Also, the global attractor of gNSE with linear dampness on 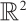 were proved, and the estimation of dimensions was also obtained in Ref. [21]. We investigated the existence of a pullback attractor for the 2D non-autonomous gNSE on the bounded domains in Ref. [22]. Quyet proved the existence of a pullback attractor in Vg for the process in Ref. [23]. Recently, we have discussed the uniform attractor and pullback attractor of gNSE with damping and time delay in Refs. [24-26], and obtained the uniform attractor and pullback attractor using the method of the energy equation and the pullback condition, respectively.
were proved, and the estimation of dimensions was also obtained in Ref. [21]. We investigated the existence of a pullback attractor for the 2D non-autonomous gNSE on the bounded domains in Ref. [22]. Quyet proved the existence of a pullback attractor in Vg for the process in Ref. [23]. Recently, we have discussed the uniform attractor and pullback attractor of gNSE with damping and time delay in Refs. [24-26], and obtained the uniform attractor and pullback attractor using the method of the energy equation and the pullback condition, respectively.
It is well-known that the research of global attractors is an important problem in infinite-dimensional dynamical systems (IDDS). In addition, the dimension is a very important property of the global attractor. However, as far as we know, the global attractor of 2D autonomous gNSE with damping and delay has been studied rarely. Therefore, in this article, we research global attractor of the 2D autonomous gNSE, which has nonlinear damping and time delay on some bounded domain 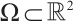 , and its usual form is as follows:
, and its usual form is as follows:
where  denotes the pressure and
denotes the pressure and 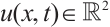 as the velocity,
as the velocity, 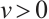 and
and 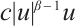 are nonlinear dampings,
are nonlinear dampings, 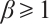 and
and 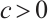 are constants,
are constants, 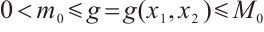 , where
, where 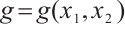 is a real-valued smooth function.
is a real-valued smooth function. 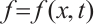 is the external force,
is the external force, 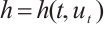 is another external force term with time delay,
is another external force term with time delay, 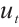 is the function which can be defined by
is the function which can be defined by 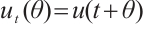 .
. 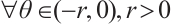 is a constant.
is a constant.
Definition 1[26] Let 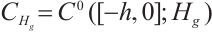 ,
, 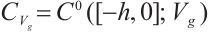 ,
,  satisfies the following assumptions:
satisfies the following assumptions:
(I) 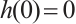 ;
;
(II) there exists 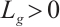 , such that
, such that 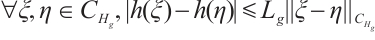 ;
;
(III) there exists 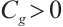 , such that
, such that 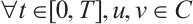
Definition 2[26] Let 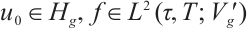 ,
, 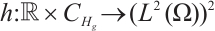 satisfies (I)-(III).
satisfies (I)-(III).
For any 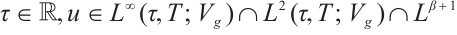
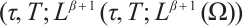 ,
, 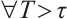 is called a weak solution of (2) if it fulfills
is called a weak solution of (2) if it fulfills
Theorem 1[26] Let 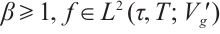 ,
, 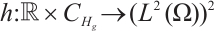 satisfies (I)-(III), then for every
satisfies (I)-(III), then for every 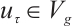 , equation (2) has the only weak solution
, equation (2) has the only weak solution 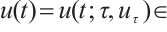
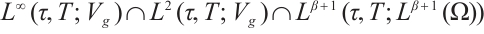 , and
, and 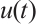 continuously depends on the initial value in
continuously depends on the initial value in 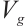 .
.
The main results of this article are as follows:
Lemma 1 For any 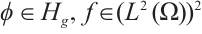 , let
, let 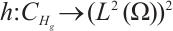 and satisfy (I)-(III), then
and satisfy (I)-(III), then 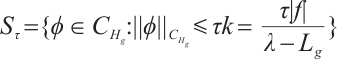 is positive invariant set of
is positive invariant set of 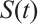 , where
, where 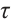 is a constant and
is a constant and 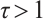 .
.
Lemma 2 For any 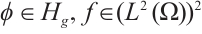 , let
, let 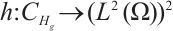 and satisfy (I)-(III), then
and satisfy (I)-(III), then 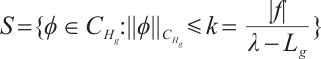 is a global absorbed set of
is a global absorbed set of 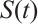 in
in 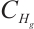 .
.
Lemma 3 For any 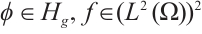 , let
, let  and satisfy (I)-(III), and
and satisfy (I)-(III), and 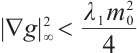 , then
, then 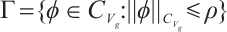 is a global absorbed set of
is a global absorbed set of 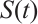 in
in 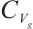 , where
, where 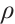 is a given constant.
is a given constant.
Theorem 2 For any 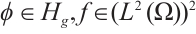 , let
, let 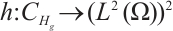 and satisfy (I)-(III), then equation (2) possesses a global attractor
and satisfy (I)-(III), then equation (2) possesses a global attractor 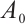 in
in 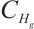 , which is compact and connected in
, which is compact and connected in 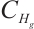 , and it attracts any bounded set in
, and it attracts any bounded set in 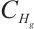 .
.
Theorem 3 Let 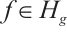 , then the semigroup
, then the semigroup 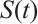 corresponding to equation (2) has a global attractor
corresponding to equation (2) has a global attractor 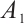 in
in 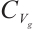 satisfying
satisfying
1) 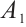 is compact in
is compact in 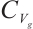 ;
;
2) 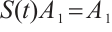 ;
;
3) For any bounded subset 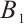 of
of 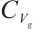 ,
,
Lemma 4 Let 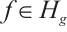 and
and 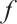 be sufficiently small, B is bounded subset in
be sufficiently small, B is bounded subset in 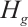 . Let
. Let 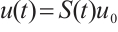 be a corresponding solution to equation (2),
be a corresponding solution to equation (2), 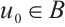 , then there exist
, then there exist 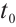 and constant
and constant 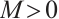 , such that
, such that  .
.
Theorem 4 Let 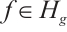 and
and 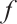 be sufficiently small, then
be sufficiently small, then 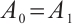 , where
, where 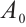 and
and 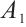 denote global attractors in
denote global attractors in 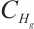 and
and 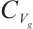 , respectively.
, respectively.
This article is organized as follows. In Section 1, we give some results on the classical theory of the global attractor. In Section 2, we obtain the global attractor of 2D gNSE with damping and time delay. In Section 3, we give some relevant conclusions.
1 Preliminaries
We define 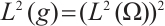 and
and 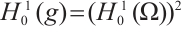 , the inner product of
, the inner product of 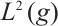 is
is 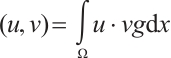 and inner product of
and inner product of 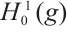 is
is 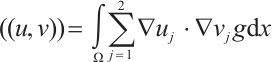 , corresponding norm is
, corresponding norm is 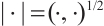 and
and 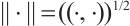 respectively.
respectively.
Let 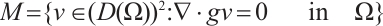 and
and 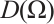 is the space of
is the space of 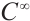 functions that have compact support contained in
functions that have compact support contained in 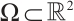 .
. 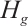 is the closure of M in
is the closure of M in 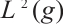 which is endowed with the inner product and norm of
which is endowed with the inner product and norm of 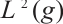 ,
, 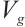 is the closure of M in
is the closure of M in 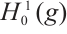 endowed with the inner product and norm of
endowed with the inner product and norm of 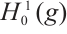 .
.
Let 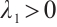 , we have
, we have
then
The g-Laplacian operator is defined as follows:
The first formula in (2) can be expressed as follows:
The g-orthogonal projection is defined by 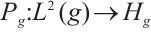 and g-Stokes operator is defined by
and g-Stokes operator is defined by 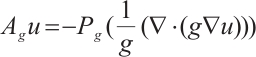 . Applying the projection
. Applying the projection 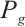 to (2), for
to (2), for 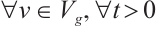 , we obtain
, we obtain
where 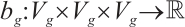 and
and 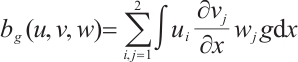 ,
, 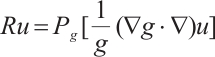 ,
, 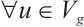 . We define
. We define 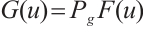 and
and 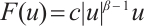 , then the formulations (6) and (7) are equivalent to the following equations
, then the formulations (6) and (7) are equivalent to the following equations
where 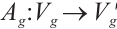 , for
, for  , we have
, we have 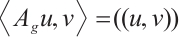 .
. 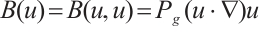 is a bilinear operator, and
is a bilinear operator, and 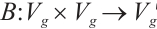 with
with 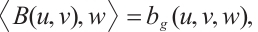
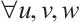
For any 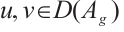 , we have
, we have 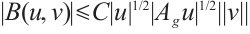 , where C denotes positive constant. From Refs. [10,17,19, 27], we have the following inequality:
, where C denotes positive constant. From Refs. [10,17,19, 27], we have the following inequality:
Definition 3[28] Let M be a complete metric space, a parameter family 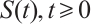 of maps
of maps 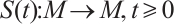 is called
is called 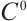 semigroup if
semigroup if
1) 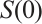 is the identity map on M,
is the identity map on M,
2) 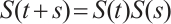 for all
for all 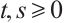 ,
,
3) the function 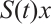 is continuous at each point
is continuous at each point 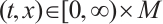 .
.
Definition 4[28] Let 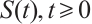 be a
be a 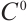 semigroup in a complete metric space M.
semigroup in a complete metric space M.
A subset 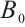 of M is called an absorbing set in M, if for any bounded subset B of M, there exists some
of M is called an absorbing set in M, if for any bounded subset B of M, there exists some 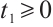 , such that
, such that 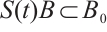 , for all
, for all 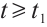 .
.
Definition 5[28] Let 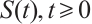 be a
be a 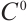 semigroup in a complete metric space M.
semigroup in a complete metric space M.
A subset 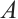 of M is called a global attractor for the semigroup if
of M is called a global attractor for the semigroup if 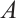 is compact and enjoys the following properties:
is compact and enjoys the following properties:
1) 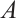 is an invariant set, i.e.,
is an invariant set, i.e., 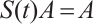 for any
for any 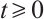 ;
;
2) 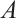 attracts all bounded sets of M. That is, for any bounded subset B of M,
attracts all bounded sets of M. That is, for any bounded subset B of M, 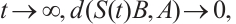 where
where  is the semidistance of two sets
is the semidistance of two sets 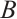 and
and 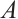 :
: 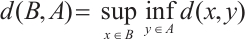 .
.
Theorem 5[28] If 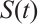 is dissipative and
is dissipative and 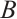 is a compact absorbing set, then there exists a global attractor
is a compact absorbing set, then there exists a global attractor 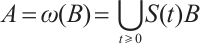 .
.
2 Proofs of the Main Results
In this section, we will obtain the global attractors of 2D gNSE in 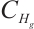 and
and 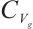 respectively.
respectively.
Proof of Lemma 1 Taking the inner product of
with u, we have
that is
For any 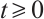 , by the Growall inequality, we obtain
, by the Growall inequality, we obtain 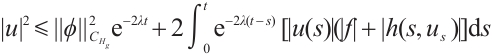
For 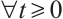 , in the following we will prove
, in the following we will prove 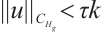 when
when 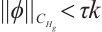 .
.
We do this by contradiction. Suppose there exists 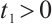 , such that
, such that 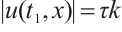 . When
. When 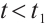 , we have
, we have 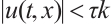 , that is, for any
, that is, for any 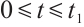 , we have
, we have 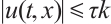 .
.
It can be obtained from the above formula that for any 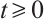 , we deduce
, we deduce
This is a contradiction, so 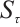 is a positive invariant set.
is a positive invariant set.
Proof of Lemma 2 For any 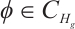 , there exists
, there exists 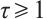 , such that
, such that 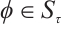 . From Lemma 1, we have
. From Lemma 1, we have 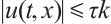 , so there exists
, so there exists 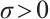 , such that
, such that 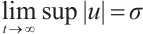 .
.
For arbitrarily small 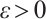 , there exists
, there exists 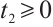 , such that
, such that 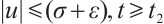 .
.
For 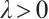 , for the above
, for the above 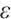 and
and 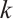 , we have
, we have 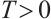 and
and 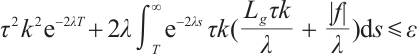 .
.
Hence, as 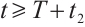 ,
,
Let 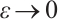 , then
, then 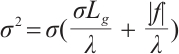 , therefore
, therefore 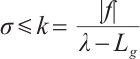 , that is,
, that is, 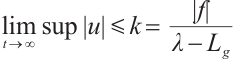 , so
, so 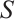 is the global absorbed set of the semigroup
is the global absorbed set of the semigroup 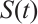 in
in 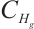 .
.
Proof of Lemma 3 Taking the inner product of (8) with 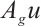 ,
,
Since 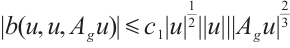
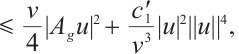 where
where 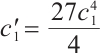 ,
,
Then
we have
For any 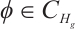 , from Lemma 1, there exists
, from Lemma 1, there exists 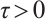 , such that
, such that 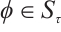 , that is, for any
, that is, for any  , we have
, we have 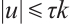 . From (8) and
. From (8) and 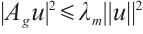 ,
,
where 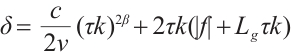 .
.
For any 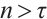 , as
, as 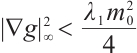 , let
, let 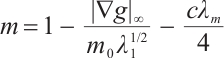 , obviously
, obviously 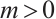 , then
, then 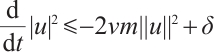 .
.
Multiply the above equation in 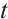 to
to 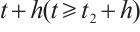 , then we have
, then we have
so 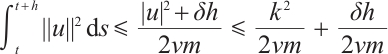 . From (14) we obtain
. From (14) we obtain 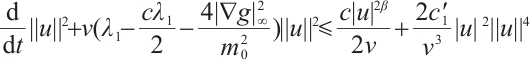
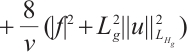 , as
, as 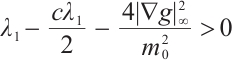 , that is
, that is 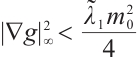 , where
, where 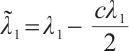 . From the above formula, we obtain
. From the above formula, we obtain
According to the uniform Gronwall lemma, we have
where 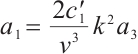 ,
, 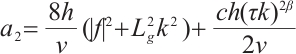 ,
, 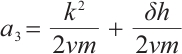 .
.
Fixed 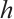 , then
, then 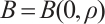 is absorbed set in
is absorbed set in 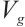 . If
. If 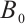 is any bounded set in
is any bounded set in 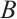 , then
, then  , we obtain
, we obtain 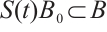 .
.
Proof of Theorem 2 From Lemmas 1-3, we have a bounded absorbing set of (2) in 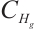 , and embedded
, and embedded 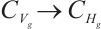 is compact. From the classical existence theorem of attractors, a global attractor of the equation (2) is proved in
is compact. From the classical existence theorem of attractors, a global attractor of the equation (2) is proved in 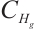 .
.
The proof of Theorem 3 is similar to that of Theorem 2. Here we omit the detailed proof.
Proof of Lemma 4 Using 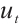 to take inner product with
to take inner product with 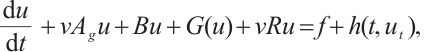 we have
we have
where 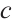 is any constant. Therefore
is any constant. Therefore
Thus
Since 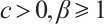 , as
, as  is sufficiently small, we make
is sufficiently small, we make 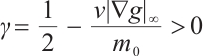 , that is
, that is 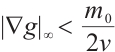 , we get
, we get
where 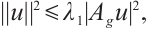
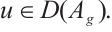 Using
Using 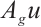 to take inner product with
to take inner product with 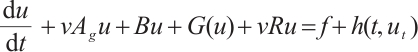 , we obtain
, we obtain 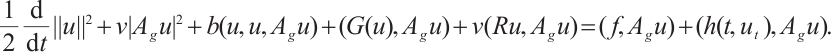 Since
Since 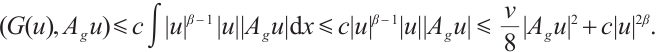
Therefore
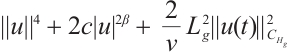 , then
, then
Integrating both sides of 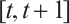 , when
, when 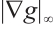 is sufficiently small, let
is sufficiently small, let 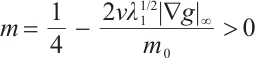 , that is
, that is 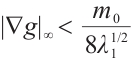 , we have
, we have
Then
From (15), we have 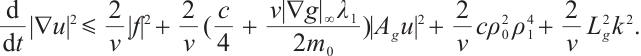
Integrating both sides of 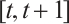 ,
, 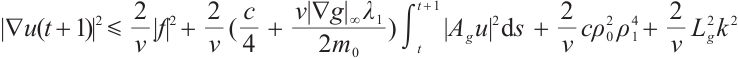
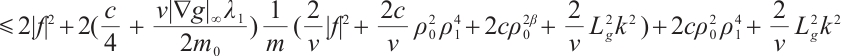 . Taking a constant
. Taking a constant 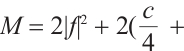
Proof of Theorem 4 Obviously 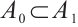 ,
, 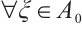 , from Theorem 3, for any
, from Theorem 3, for any 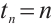 , we have
, we have 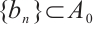 and
and 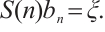
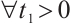 , since
, since 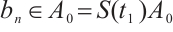 , so
, so 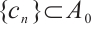 , we have
, we have 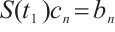 . As
. As 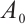 is compact in
is compact in 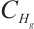 , by Lemma 4 and
, by Lemma 4 and 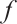 is sufficiently small, we obtain that
is sufficiently small, we obtain that 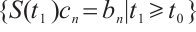 is a bounded subset in
is a bounded subset in 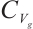 , therefore
, therefore 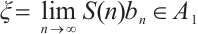 . For
. For 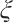 is arbitrary, we have
is arbitrary, we have 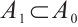 , then
, then 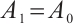 .
.
3 Conclusion
In this article, we study how to control the nonlinear dampness 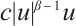 and time delay
and time delay 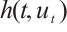 to obtain the global attractor of the 2D gNSE on a bounded domain. We find that the global absorbing sets exist in
to obtain the global attractor of the 2D gNSE on a bounded domain. We find that the global absorbing sets exist in 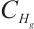 when
when 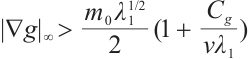 , and exist in
, and exist in 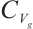 when
when 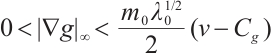 . We obtain the global attractor by the compact embedding method and find that the attractor has an asymptotic smoothing effect. The conclusions of this paper will further promote the research of NSE. It is necessary to study gNSE systematically. In the future, we may consider the global attractor 2D gNSE with damping and delay on the unbounded domain.
. We obtain the global attractor by the compact embedding method and find that the attractor has an asymptotic smoothing effect. The conclusions of this paper will further promote the research of NSE. It is necessary to study gNSE systematically. In the future, we may consider the global attractor 2D gNSE with damping and delay on the unbounded domain.
References
- Abergel F. Attractor for a Navier-Stokes flow in an unbounded domain[J]. ESAIM: Mathematical Modelling and Numerical Analysis, 1989, 23(3): 359-370. [Google Scholar]
- Babin A V. The attractor of a Navier-Stokes system in an unbounded channel-like domain[J]. Journal of Dynamics and Differential Equations, 1992, 4(4): 555-584. [Google Scholar]
- Rosa R. The global attractor for the 2D Navier-Stokes flow on some unbounded domains[J]. Nonlinear Analysis: Theory, Methods & Applications, 1998, 32(1): 71-85. [Google Scholar]
- Cheban D, Duan J Q. Almost periodic solutions and global attractors of non-autonomous Navier-Stokes equations[J]. Journal of Dynamics and Differential Equations, 2004, 16(1): 1-34. [Google Scholar]
- Hou Y R, Li K T. The uniform attractor for the 2D non-autonomous Navier-Stokes flow in some unbounded domain[J]. Nonlinear Analysis: Theory, Methods & Applications, 2004, 58(5/6): 609-630. [Google Scholar]
- Caraballo T, Lukaszewicz G, Real J. Pullback attractors for asymptotically compact non-autonomous dynamical systems[J]. Nonlinear Analysis: Theory, Methods & Applications, 2006, 64(3): 484-498. [Google Scholar]
- Wang Y J, Zhong C K, Zhou S F. Pullback attractors of nonautonomous dynamical systems[J]. Discrete & Continuous Dynamical Systems - A, 2006, 16(3): 587-614. [Google Scholar]
- Cai X J, Jiu Q S. Weak and strong solutions for the incompressible Navier-Stokes equations with damping[J]. Journal of Mathematical Analysis and Applications, 2008, 343(2): 799-809. [Google Scholar]
- Zhang Z J, Wu X L, Lu M. On the uniqueness of strong solution to the incompressible Navier-Stokes equations with damping[J]. Journal of Mathematical Analysis and Applications, 2011, 377(1): 414-419. [Google Scholar]
- Jia Y, Zhang X W, Dong B Q. The asymptotic behavior of solutions to three-dimensional Navier-Stokes equations with nonlinear damping[J]. Nonlinear Analysis: Real World Applications, 2011, 12(3): 1736-1747. [Google Scholar]
- Jiang Z H, Zhu M X. The large time behavior of solutions to 3D Navier-Stokes equations with nonlinear damping[J]. Mathematical Methods in the Applied Sciences, 2012, 35(1): 97-102. [Google Scholar]
- Song X L, Hou Y R. Attractors for the three-dimensional incompressible Navier-Stokes equationswith damping[J]. Discrete & Continuous Dynamical Systems - A, 2011, 31(1): 239-252. [Google Scholar]
- Caraballo T, Real J. Asymptotic behaviour of two-dimensional Navier-Stokes equations with delays[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 2003, 459(2040): 3181-3194. [Google Scholar]
- Taniguchi T. The exponential behavior of Navier-Stokes equations with time delay external force[J]. Discrete & Continuous Dynamical Systems - A, 2005, 12(5): 997-1018. [Google Scholar]
- Marín-Rubio P, Real J, Valero J. Pullback attractors for a two-dimensional Navier-Stokes model in an infinite delay case[J]. Nonlinear Analysis: Theory, Methods & Applications, 2011, 74(5): 2012-2030. [Google Scholar]
- Caraballo T, Han X Y. A survey on Navier-Stokes models with delays: Existence, uniqueness and asymptotic behavior of solutions[J]. Discrete & Continuous Dynamical Systems - S, 2015, 8(6): 1079-1101. [Google Scholar]
- Roh J. g-Navier-Stokes Equations[D]. Minneapolis: University of Minnesota, 2001. [Google Scholar]
- Bae H, Roh J. Existence of solutions of the g-Navier-Stokes equations[J]. Taiwanese J Math, 2004, 8(1): 85-102. [Google Scholar]
- Roh J. Dynamics of the g-Navier-Stokes equations[J]. Journal of Differential Equations, 2005, 211(2): 452-484. [Google Scholar]
- Kwak M, Kwean H, Roh J. The dimension of attractor of the 2D g-Navier-Stokes equations[J]. Journal of Mathematical Analysis and Applications, 2006, 315(2): 436-461. [Google Scholar]
-
Jiang J P, Hou Y R. The global attractor of g-Navier-Stokes equations with linear dampness on
 2[J]. Applied Mathematics and Computation, 2009, 215(3): 1068-1076.
[Google Scholar]
2[J]. Applied Mathematics and Computation, 2009, 215(3): 1068-1076.
[Google Scholar]
- Jiang J P, Hou Y R. Pullback attractor of 2D non-autonomous g-Navier-Stokes equations on some bounded domains[J]. Applied Mathematics and Mechanics (English Edition), 2010, 31(6): 697-708. [Google Scholar]
- Quyet D T. Pullback attractors for strong solutions of 2D non-autonomous g-Navier-Stokes equations[J]. Acta Mathematica Vietnamica, 2015, 40(4): 637-651. [Google Scholar]
- Wang X X, Jiang J P. The long-time behavior of 2D nonautonomous g-Navier-Stokes equations with weak dampness and time delay[J]. Journal of Function Spaces, 2022, 2022: 1-11. [Google Scholar]
- Wang X X, Jiang J P. The uniform asymptotic behavior of solutions for 2D g-Navier-Stokes equations with nonlinear dampness and its dimensions[J]. Electronic Research Archive, 2023, 31(7): 3963-3979. [Google Scholar]
- Wang X X, Jiang J P. The pullback attractor for the 2D g-Navier-Stokes equation with nonlinear damping and time delay[J]. AIMS Mathematics, 2023, 8(11): 26650-26664. [Google Scholar]
- Hale J K. Asymptotic Behaviour of Dissipative Dynamical Systems[M]. Providence: Amer Math Soc, 1988. [Google Scholar]
- Robinson J C. Infinite-Dimensional Dynamical Systems: An Introduction to Dissipative Parabolic PDEs and the Theory of Global Attractors[M]. Cambridge: Cambridge University Press, 2001. [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.