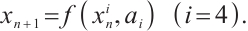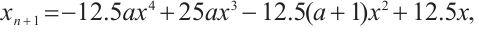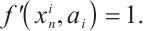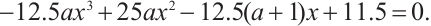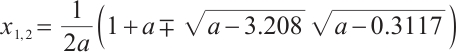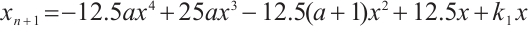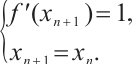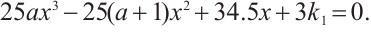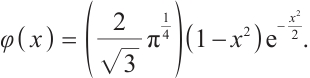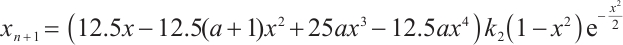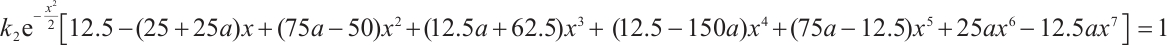| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
|
|
|---|---|---|
| Page(s) | 276 - 282 | |
| DOI | https://doi.org/10.1051/wujns/2025303276 | |
| Published online | 16 July 2025 | |
Mathematics
CLC number: O193
Chaotic Analysis and Control of a Two-Peak Discrete Chaotic System
一个双峰离散混沌系统的混沌分析和控制
1 School of Intelligent Manufacturing, Jianghan University, Wuhan 430056, Hubei, China
2 College of Mechanical and Electrical Engineering, Wuhan Qingchuan University, Wuhan 430204, Hubei, China
Received:
11
May
2024
The nonlinear dynamic characteristics of a two-peak discrete chaotic system are studied. Through the study of the nonlinear dynamic behavior of the system, it is found that with the change of the system parameters, the system starts from a chaotic state, and then goes through intermittent chaos, stable region, period-doubling bifurcation to a chaotic state again. The system's critical conditions and process to generate intermittent chaos are analyzed. The feedback control method sets linear and nonlinear controllers for the system to control the chaos. By adjusting the value of control parameters, the intermittent chaos can be delayed or disappear, and the stability region and period-doubling bifurcation process of the system can be expanded. Both linear controllers and nonlinear controllers have the same control effect. The numerical simulation analysis verifies the correctness of the theoretical analysis.
摘要
本文研究了一个双峰离散混沌系统的非线性动力学特性。通过对系统非线性动力学行为的研究,发现随着系统参数的变化,系统从混沌状态开始,然后经历阵发混沌、稳定状态、倍周期分岔,再次进入混沌状态。分析了系统产生阵发混沌的临界条件和过程。反馈控制方法用于为系统设置线性控制器和非线性控制器来控制混沌。通过调整控制参数的值,可以延迟或消除阵发混沌,扩展系统的稳定区域和倍周期分岔过程。线性控制器和非线性控制器具有相同的控制效果。数值模拟分析验证了理论分析的正确性。
Key words: two-peak discrete chaotic system / intermittent chaos / linear controller / nonlinear controller / chaos control
关键字 : 双峰离散混沌系统 / 阵发混沌 / 线性控制器 / 非线性控制器 / 混沌控制
Cite this article: ZHANG Liang, HAN Qin. Chaotic Analysis and Control of a Two-Peak Discrete Chaotic System[J]. Wuhan Univ J of Nat Sci, 2025, 30(3): 276-282.
Biography: ZHANG Liang, male, Associate professor, research direction: bifurcation analysis and control of dynamical systems. E-mail: lzhang08@163.com
Foundation item: Supported by the Guiding Project of Science and Technology Research Plan of Hubei Provincial Department of Education (B2022458)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Chaos exists in all aspects of nature, such as chemical engineering[1-2], mechanical engineering[3-4], and biological engineering[5-6]. Chaos is a unique motion state of some nonlinear systems, with unstable attractors. Namely, the motion state of the nonlinear dynamic system is unstable and then bifurcates, and finally enters into the chaotic state. In recent decades, chaos has been one of the important contents of nonlinear scientific research.
The dynamic analysis of new discrete chaotic systems has become one of the research directions in nonlinear scientific research[7-12]. By conducting dynamic analysis on discrete chaotic systems, the periodic and chaotic solutions of the system are obtained, which enter the chaotic system through a doubling bifurcation process[7-9]. Nategh et al[8] analyzed the dynamic of delayed discrete chaotic systems with delay. Time delay appears in an additive form. By analyzing the dynamics of time-delay discrete chaotic systems, it is found that the system is neutral to bounded delays and has attractive fixed points in both additive and non-additive forms. Chen et al[10] analyzed a predator-prey discrete chaotic system. Using the new paradigm, central manifold theorem, and bifurcation theory of discrete singular systems, the occurrence of flipping bifurcation and Neimark Sacker bifurcation in the system was analyzed. This discrete chaotic system has rich dynamic characteristics. Dai et al[12] generated a discrete chaotic system using fractal transformation. The dynamic characteristics of this discrete chaotic system were analyzed from the aspects of bifurcation, complexity, and spectral distribution characteristics. The discrete chaotic system was verified with circuits. These studies indicate that discrete chaotic systems have rich nonlinear dynamic characteristics and can be applied in engineering, such as biotechnology[10], communication encryption[12-13], etc.
The chaos control of discrete chaotic systems is another important direction in nonlinear scientific research. The main contents of chaos control in discrete chaotic systems include synchronization control[14-16], bifurcation control[17-18], and others[19-21]. Yong et al[14] proposed a control method based on the backstepping design of three controllers to study the function projection synchronization of discrete-time chaotic systems with uncertain parameters. Zhang et al[15] used a pulse controller to perform lag synchronization control on a discrete chaotic system, obtaining sufficient conditions for synchronization between the driving system and the response system. Zhang et al[17] analyzed and controlled the symmetry-breaking bifurcation of cubic discrete chaos, and obtained the cause of the symmetry-breaking bifurcation. A controller was set for the system to make the symmetry-breaking bifurcation disappear and the period-doubling bifurcation recover. Din[19] studied a discrete-time predator-prey system and analyzed its dynamic characteristics, such as boundedness, existence, and bifurcation. The feedback control method was used to delay the generation of bifurcation and avoid chaos. Tang et al[20] used neural network control methods to control chaos in a class of discrete chaotic systems. This method can generate the optimal control input and effectively make the system bounded. These studies rarely involve the control of intermittent chaos and period-doubling bifurcation in discrete chaotic systems, and even less so for two-peak discrete chaotic systems. In this paper, the dynamic characteristics of a two-peak discrete chaotic system are analyzed to verify the causes of intermittent chaos. Linear and nonlinear state feedback controllers are set up for the discrete chaotic system to control the chaos, to delay the generation of bifurcations, and to expand the stability range of the system. The goal of chaos control is achieved.
The paper is arranged as follows: In Section 1, the dynamic characteristics of the two-peak discrete chaotic system are analyzed to obtain the system motion process. In Section 2, the conditions of intermittent chaos are analyzed, and the motion process of intermittent chaos is expounded. In Section 3, linear controllers and nonlinear controllers are set to the system to delay or eliminate chaos. Finally, Section 4 summarizes this paper.
1 Two-Peak Discrete Chaotic System
When a discrete chaotic system exhibits two chaotic states, this discrete chaotic system is called a two-peak discrete chaotic system. Two-peak discrete chaotic systems are generally composed of high-power chaotic systems, and their coefficients can be determined by specific conditions. The nonlinear dynamic model of a two-peak discrete chaotic system is as follows:
We can write the general iteration of (1) as follows:
where  .
.
By taking the system parameter 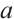 as the bifurcation parameter, bifurcation can be obtained by numerical calculation of system formula (2) when the initial value
as the bifurcation parameter, bifurcation can be obtained by numerical calculation of system formula (2) when the initial value 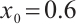 , as shown in Fig. 1.
, as shown in Fig. 1.
 |
Fig. 1 Bifurcation diagram |
From Fig. 1, we can see the system state movement process. The system starts from a chaotic state, goes through intermittent chaos, a stable state, period-doubling bifurcation, and then goes through a transient stable state, and finally enters an intermittent chaotic state again. The two-peak discrete chaotic system is that within the range of the system parameters, the system appears the secondary chaotic state in the process of motion. This bifurcation diagram just verifies this definition.
To better understand the nonlinear dynamic behavior of two-peak discrete chaotic systems, we draw the Lyapunov exponent spectrum of two-peak discrete chaotic systems, as shown in Fig. 2.
 |
Fig. 2 Lyapunov exponents of the system (2) |
It can be seen from Fig. 2 that the shape of the Lyapunov exponent spectrum changes with the change of system parameter 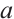 . When
. When 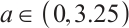 , the system (2) is in intermittent chaos. There are periodic windows in the process. When
, the system (2) is in intermittent chaos. There are periodic windows in the process. When 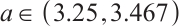 , the system enters a stable state and is in one period. When
, the system enters a stable state and is in one period. When 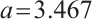 , the system enters the period-doubling bifurcation state, one period is divided into two periods. When
, the system enters the period-doubling bifurcation state, one period is divided into two periods. When 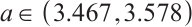 , the system continues to be in the period-doubling bifurcation state, which is divided into four periods from two periods and eight periods from four periods. When
, the system continues to be in the period-doubling bifurcation state, which is divided into four periods from two periods and eight periods from four periods. When 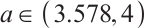 , the system enters a chaotic state.
, the system enters a chaotic state.
The motion process of the two-peak discrete chaotic system (2) can also be seen from the waveform of the system. The system from an unstable state to a stable state, then to a stable periodic solution, and finally to an unstable state. The waveform is shown in Fig. 3.
 |
Fig. 3 Waveform diagram |
2 Intermittent Chaos
Period doubling bifurcation is one of the ways in which the system enters chaos. When the system exhibits chaotic formation, the system is unstable and lacks periodic solutions. The system is in a chaotic state. The critical condition for the system to generate intermittent chaos is the system parameter value when the system angular line is tangent to the two-peak discrete chaotic system (2). According to the reasoning of the tangent equation in equation (2), when the tangent equation passes through the origin and the slope 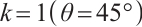 , the chaotic system is in a critical state, and the tangent point is a fixed point. At this time, the system parameter
, the chaotic system is in a critical state, and the tangent point is a fixed point. At this time, the system parameter 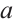 value is a critical condition. From the condition of the fixed point, we get
value is a critical condition. From the condition of the fixed point, we get
When the two-peak discrete chaotic system (2) is tangent to the angular line, there is 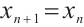 . Namely,
. Namely,
By solving equations (3) and (4), we can get the iterative algebraic value 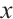 and system parameters of the chaotic system (2) when it is tangent to the diagonal line. The quadratic function relationship of iteration value
and system parameters of the chaotic system (2) when it is tangent to the diagonal line. The quadratic function relationship of iteration value 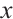 and system parameters
and system parameters 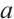 is:
is:
We substitute the two conditions of equation (5) back to equation (4) to obtain the critical values of a two-peak discrete chaotic system. The critical values are 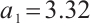 and
and 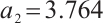 . The calculated critical values are the same as the occurrence of intermittent chaos in the bifurcation diagram in Fig. 1.
. The calculated critical values are the same as the occurrence of intermittent chaos in the bifurcation diagram in Fig. 1.
Next, we analyze the dynamic characteristics of intermittent chaos. The local bifurcation of the system (2) is shown in Fig. 4.
 |
Fig. 4 Local bifurcation diagram |
In Fig. 4, the evacuation area with fewer values in the chaotic area is an intermittent chaotic process. In the process of numerical iteration, the number of iterations around the fixed point is far greater than that of the intermittent chaotic process, then there are two chaotic regions: evacuation and dense. It can be seen from the figure that when the system parameter 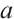 gradually increases, the evacuation area gradually decreases, the numerical range of the intermittent chaotic process gradually narrows, and the iterative process becomes shorter. This shows that the distance between
gradually increases, the evacuation area gradually decreases, the numerical range of the intermittent chaotic process gradually narrows, and the iterative process becomes shorter. This shows that the distance between 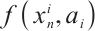 and the angular line
and the angular line 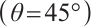 is getting closer and closer. Finally,
is getting closer and closer. Finally, 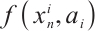 is tangent to the angular line
is tangent to the angular line 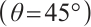 , and the system changes from intermittent chaos to a stable fixed point.
, and the system changes from intermittent chaos to a stable fixed point.
The local Lyapunov exponents of the system (2) are shown in Fig. 5. From the figure, we can see that there are two chaotic windows in intermittent chaos, which indicates that the process of intermittent chaos also includes chaos and periodic motion. The motion process of the system starts from intermittent chaos to period-doubling bifurcation. Figure 6 shows the fine structure of the window chaotic behavior.
 |
Fig. 5 Local Lyapunov exponents |
 |
Fig. 6 Fine structure of window chaotic behavior |
3 Chaos Control
One of the purposes of chaos control is to change the position where chaos occurs so that the position where chaos occurs is delayed or advanced. We set linear controllers and nonlinear controllers for system (2) to change the position of intermittent chaos.
3.1 Linear Controllers
Set linear controllers for the system (2) without changing the system equilibrium point. The controlled system is as follows:
where 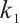 is the control parameter.
is the control parameter.
According to the critical condition of intermittent chaos, we can get
Through detailed calculation, we can get the relationship between the system parameter 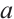 and the control parameter
and the control parameter 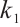 :
:
Set 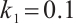 , then
, then 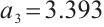 and
and 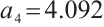 . Similar to the system (2), the positions of intermittent chaos are delayed.
. Similar to the system (2), the positions of intermittent chaos are delayed.
From the bifurcation diagram (Fig. 7) and Lyapunov exponential diagram (Fig. 8) of the system (6), we can see that the dynamic characteristics of the system have changed. The experience time of intermittent chaos of the system becomes shorter, and the critical point from intermittent chaos to a stable state is delayed from 3.32 to 3.39. When 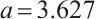 , the system is divided into two periodic states from one periodic state, and then into four periodic states, until it enters a chaotic state. When
, the system is divided into two periodic states from one periodic state, and then into four periodic states, until it enters a chaotic state. When 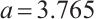 , the system jumps, and the system goes from chaos to stability. When
, the system jumps, and the system goes from chaos to stability. When 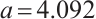 , the system jumps into intermittent chaos. Under the effect of the control parameter
, the system jumps into intermittent chaos. Under the effect of the control parameter 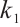 , intermittent chaos becomes narrower with the increase of system parameter
, intermittent chaos becomes narrower with the increase of system parameter 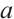 .
.
 |
Fig. 7 Bifurcation diagram of the system (6) when 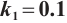
|
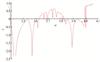 |
Fig. 8 Lyapunov exponents of the system (6) when 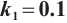
|
Set 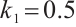 , the intermittent chaos of the system (6) is disappeared. The motion process of the system is in a stable state. After the period-doubling bifurcation, it finally enters a chaotic state, as shown in Fig. 9.
, the intermittent chaos of the system (6) is disappeared. The motion process of the system is in a stable state. After the period-doubling bifurcation, it finally enters a chaotic state, as shown in Fig. 9.
 |
Fig. 9 Bifurcation diagram of the system (6) when 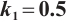
|
3.2 Nonlinear Controller
The wavelet function is an important nonlinear controller. Wavelet functions have oscillatory properties. As the independent variable continues to extend in the positive and negative directions, the wavelet function rapidly decays. As a controller for chaotic systems, wavelet functions can suppress the chaotic behavior of the system. Due to the non or thogonality and scale function of the Metican wavelet function, it has good localization properties in both the time and frequency domains, while satisfying the requirement of zero infinite integration on all real number intervals. Therefore, the metric wavelet function is chosen as the nonlinear controller of the system.
The mathematical expression for the metric wavelet function is
To obtain more control results, the coefficients of the wavelet function are set to the gain coefficient 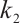 . By adjusting the value of the gain coefficient
. By adjusting the value of the gain coefficient 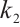 , chaos control of the system (1) is achieved.
, chaos control of the system (1) is achieved.
The controlled system is as follows:
where 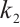 is the control parameter.
is the control parameter.
According to equation (7), the relationship between the system parameter 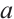 and the control parameter
and the control parameter 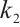 is obtained.
is obtained.
Set 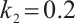 , the bifurcation diagram and Lyapunov exponential diagram of the system are shown in Fig. 10 and Fig. 11.
, the bifurcation diagram and Lyapunov exponential diagram of the system are shown in Fig. 10 and Fig. 11.
 |
Fig.10 Bifurcation diagram of the system (10) when 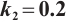
|
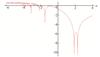 |
Fig.11 Lyapunov exponents of the system (10) when 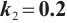
|
From Fig. 10 and Fig. 11, it can be seen that the intermittent chaos of the system (10) is disappeared. The controlled system only has one process of transitioning from period-doubling bifurcation to chaos. The system has two chaotic processes, only one of which enters chaos through period-doubling bifurcation. When 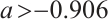 , the system is in a stable state. When
, the system is in a stable state. When 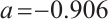 , the system has period-doubling bifurcation. The system is divided into two periodic states from one periodic state, and then into four periodic states, eight periodic states, until enters a chaotic state. Under the action of a nonlinear controller, the system transitions from two complex chaotic processes to a process of transitioning from period-doubling bifurcation to chaos. The direction of the period-doubling bifurcation of the controlled system changes, becoming an inverted bifurcation. The critical value of bifurcation is less than 0, and the occurrence of chaos is delayed, expanding the stability range of the system.
, the system has period-doubling bifurcation. The system is divided into two periodic states from one periodic state, and then into four periodic states, eight periodic states, until enters a chaotic state. Under the action of a nonlinear controller, the system transitions from two complex chaotic processes to a process of transitioning from period-doubling bifurcation to chaos. The direction of the period-doubling bifurcation of the controlled system changes, becoming an inverted bifurcation. The critical value of bifurcation is less than 0, and the occurrence of chaos is delayed, expanding the stability range of the system.
Set 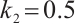 , the system has returned to the state of two chaotic processes, but there has been no occurrence of intermittent chaos. The bifurcation diagram and Lyapunov exponential diagram of the system are shown in Fig. 12 and Fig. 13.
, the system has returned to the state of two chaotic processes, but there has been no occurrence of intermittent chaos. The bifurcation diagram and Lyapunov exponential diagram of the system are shown in Fig. 12 and Fig. 13.
 |
Fig.12 Bifurcation diagram of the system (10) when 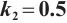
|
 |
Fig.13 Lyapunov exponents of the system (10) when 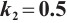
|
From Fig. 12 and Fig. 13, it can be seen that the dynamic characteristics of the controlled system (10) are the same as those of the original system (2). Just under the action of the controller, the stability range of the system changes from 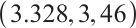 to
to 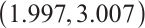 . The stable range has been expanded. Meanwhile, the intermittent chaos of the system (10) transforms into a process of period-doubling bifurcation and entering chaos.
. The stable range has been expanded. Meanwhile, the intermittent chaos of the system (10) transforms into a process of period-doubling bifurcation and entering chaos.
From the above analysis, it can be seen that wavelet functions serving as nonlinear controllers for discrete chaotic systems have good convergence. By adjusting the control parameters of the controller, the stable range of the system can be greatly expanded. Meanwhile, this nonlinear controller can transform complex paroxysmal chaotic processes into a simple process of transitioning from multiplicative bifurcation to chaos. The purpose of chaos control is realized.
4 Conclusion
In our work, the dynamic characteristics of a two-peak discrete chaotic system are studied. The conditions and process of intermittent chaos are analyzed. We set linear controller and nonlinear controller to control the chaos of the system and change the dynamic characteristics of the system. By adjusting the value of control parameters, the position of intermittent chaos in the system changes and can be delayed or disappear. Simulation analysis verifies the correctness of the theoretical analysis.
References
- Harmon Ray W, Villa C M. Nonlinear dynamics found in polymerization processes: A review[J]. Chemical Engineering Science, 2000, 55(2): 275-290. [Google Scholar]
- Wu X G, Kapral R. Internal fluctuations and deterministic chemical chaos[J]. Physical Review Letters, 1993, 70(13): 1940-1943. [Google Scholar]
- Huang K, Cheng Z B, Xiong Y S, et al. Bifurcation and chaos analysis of a spur gear pair system with fractal gear backlash[J]. Chaos, Solitons & Fractals, 2021, 142: 110387. [Google Scholar]
- Liu S X, Hu A J, Zhang Y, et al. Nonlinear dynamics analysis of a multistage planetary gear transmission system[J]. International Journal of Bifurcation and Chaos, 2022, 32(7): 2250096. [Google Scholar]
- Sen M, Srinivasu P D N, Banerjee M. Global dynamics of an additional food provided predator-prey system with constant harvest in predators[J]. Applied Mathematics and Computation, 2015, 250: 193-211. [Google Scholar]
- Zhao H Y, Huang X X, Zhang X B. Hopf bifurcation and harvesting control of a bioeconomic plankton model with delay and diffusion terms[J]. Physica A: Statistical Mechanics and Its Applications, 2015, 421: 300-315. [Google Scholar]
- Lu J N, Wu X Q, Lü J H, et al. A new discrete chaotic system with rational fraction and its dynamical behaviors[J]. Chaos, Solitons & Fractals, 2004, 22(2): 311-319. [Google Scholar]
- Nategh M, Baleanu D, Taghizadeh E, et al. Almost local stability in discrete delayed chaotic systems[J]. Nonlinear Dynamics, 2017, 89(4): 2393-2402. [Google Scholar]
- Jiang H B, Li T, Zeng X L, et al. Bifurcation analysis of the logistic map via two periodic impulsive forces[J]. Chinese Physics B, 2014, 23(1): 116-122(Ch). [Google Scholar]
- Chen B S, Chen J J. Bifurcation and chaotic behavior of a discrete singular biological economic system[J]. Applied Mathematics and Computation, 2012, 219(5): 2371-2386. [Google Scholar]
- Sokolov S, Zhilenkov A, Chernyi S, et al. Dynamics models of synchronized piecewise linear discrete chaotic systems of high order[J]. Symmetry, 2019, 11(2): 236. [Google Scholar]
- Dai S Q, Sun K H, Ai W, et al. Novel discrete chaotic system via fractal transformation and its DSP implementation[J]. Modern Physics Letters B, 2020, 34(Supp01): 2050429. [Google Scholar]
- Wang C F, Fan C L, Ding Q. Constructing discrete chaotic systems with positive Lyapunov exponents[J]. International Journal of Bifurcation and Chaos, 2018, 28(7): 1850084. [Google Scholar]
- Yong C, Xin L. Function projective synchronization in discrete-time chaotic system with uncertain parameters[J]. Communications in Theoretical Physics, 2009, 51(3): 470-474. [Google Scholar]
- Zhang L P, Jiang H B, Bi Q S. Reliable impulsive lag synchronization for a class of nonlinear discrete chaotic systems[J]. Nonlinear Dynamics, 2010, 59(4): 529-534. [Google Scholar]
- Ju H P. A new approach to synchronization of discrete-time chaotic systems[J]. Journal of the Physical Society of Japan, 2007, 76(9): 093002. [Google Scholar]
- Zhang L, Han Q. Symmetry breaking bifurcation analysis and control of a cubic discrete chaotic system[J]. The European Physical Journal Special Topics, 2022, 231(11): 2125-2131. [Google Scholar]
- Zhang L, Tang J S, Ouyang K J. Anti-control of period doubling bifurcation for a variable substitution model of Logistic map[J]. Optik, 2017, 130: 1327-1332. [Google Scholar]
- Din Q. Complexity and chaos control in a discrete-time prey-predator model[J]. Communications in Nonlinear Science and Numerical Simulation, 2017, 49: 113-134. [Google Scholar]
- Tang L, Gao Y, Liu Y J. Adaptive near optimal neural control for a class of discrete-time chaotic system[J]. Neural Computing and Applications, 2014, 25(5): 1111-1117. [Google Scholar]
- Ouannas A. A new generalized-type of synchronization for discrete-time chaotic dynamical systems[J]. Journal of Computational and Nonlinear Dynamics, 2015, 10(6): 061019. [Google Scholar]
All Figures
 |
Fig. 1 Bifurcation diagram |
| In the text | |
 |
Fig. 2 Lyapunov exponents of the system (2) |
| In the text | |
 |
Fig. 3 Waveform diagram |
| In the text | |
 |
Fig. 4 Local bifurcation diagram |
| In the text | |
 |
Fig. 5 Local Lyapunov exponents |
| In the text | |
 |
Fig. 6 Fine structure of window chaotic behavior |
| In the text | |
 |
Fig. 7 Bifurcation diagram of the system (6) when 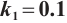
|
| In the text | |
 |
Fig. 8 Lyapunov exponents of the system (6) when 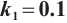
|
| In the text | |
 |
Fig. 9 Bifurcation diagram of the system (6) when 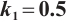
|
| In the text | |
 |
Fig.10 Bifurcation diagram of the system (10) when 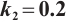
|
| In the text | |
 |
Fig.11 Lyapunov exponents of the system (10) when 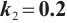
|
| In the text | |
 |
Fig.12 Bifurcation diagram of the system (10) when 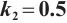
|
| In the text | |
 |
Fig.13 Lyapunov exponents of the system (10) when 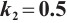
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.