EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 30 / No 3 (June 2025) Wuhan Univ. J. Nat. Sci., 30 3 (2025) 269-275 References
Open Access
Issue
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
Page(s) 269 - 275
DOI https://doi.org/10.1051/wujns/2025303269
Published online 16 July 2025
  1. Abergel F. Attractor for a Navier-Stokes flow in an unbounded domain[J]. ESAIM: Mathematical Modelling and Numerical Analysis, 1989, 23(3): 359-370. [Google Scholar]
  2. Babin A V. The attractor of a Navier-Stokes system in an unbounded channel-like domain[J]. Journal of Dynamics and Differential Equations, 1992, 4(4): 555-584. [Google Scholar]
  3. Rosa R. The global attractor for the 2D Navier-Stokes flow on some unbounded domains[J]. Nonlinear Analysis: Theory, Methods & Applications, 1998, 32(1): 71-85. [Google Scholar]
  4. Cheban D, Duan J Q. Almost periodic solutions and global attractors of non-autonomous Navier-Stokes equations[J]. Journal of Dynamics and Differential Equations, 2004, 16(1): 1-34. [Google Scholar]
  5. Hou Y R, Li K T. The uniform attractor for the 2D non-autonomous Navier-Stokes flow in some unbounded domain[J]. Nonlinear Analysis: Theory, Methods & Applications, 2004, 58(5/6): 609-630. [Google Scholar]
  6. Caraballo T, Lukaszewicz G, Real J. Pullback attractors for asymptotically compact non-autonomous dynamical systems[J]. Nonlinear Analysis: Theory, Methods & Applications, 2006, 64(3): 484-498. [Google Scholar]
  7. Wang Y J, Zhong C K, Zhou S F. Pullback attractors of nonautonomous dynamical systems[J]. Discrete & Continuous Dynamical Systems - A, 2006, 16(3): 587-614. [Google Scholar]
  8. Cai X J, Jiu Q S. Weak and strong solutions for the incompressible Navier-Stokes equations with damping[J]. Journal of Mathematical Analysis and Applications, 2008, 343(2): 799-809. [Google Scholar]
  9. Zhang Z J, Wu X L, Lu M. On the uniqueness of strong solution to the incompressible Navier-Stokes equations with damping[J]. Journal of Mathematical Analysis and Applications, 2011, 377(1): 414-419. [Google Scholar]
  10. Jia Y, Zhang X W, Dong B Q. The asymptotic behavior of solutions to three-dimensional Navier-Stokes equations with nonlinear damping[J]. Nonlinear Analysis: Real World Applications, 2011, 12(3): 1736-1747. [Google Scholar]
  11. Jiang Z H, Zhu M X. The large time behavior of solutions to 3D Navier-Stokes equations with nonlinear damping[J]. Mathematical Methods in the Applied Sciences, 2012, 35(1): 97-102. [Google Scholar]
  12. Song X L, Hou Y R. Attractors for the three-dimensional incompressible Navier-Stokes equationswith damping[J]. Discrete & Continuous Dynamical Systems - A, 2011, 31(1): 239-252. [Google Scholar]
  13. Caraballo T, Real J. Asymptotic behaviour of two-dimensional Navier-Stokes equations with delays[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 2003, 459(2040): 3181-3194. [Google Scholar]
  14. Taniguchi T. The exponential behavior of Navier-Stokes equations with time delay external force[J]. Discrete & Continuous Dynamical Systems - A, 2005, 12(5): 997-1018. [Google Scholar]
  15. Marín-Rubio P, Real J, Valero J. Pullback attractors for a two-dimensional Navier-Stokes model in an infinite delay case[J]. Nonlinear Analysis: Theory, Methods & Applications, 2011, 74(5): 2012-2030. [Google Scholar]
  16. Caraballo T, Han X Y. A survey on Navier-Stokes models with delays: Existence, uniqueness and asymptotic behavior of solutions[J]. Discrete & Continuous Dynamical Systems - S, 2015, 8(6): 1079-1101. [Google Scholar]
  17. Roh J. g-Navier-Stokes Equations[D]. Minneapolis: University of Minnesota, 2001. [Google Scholar]
  18. Bae H, Roh J. Existence of solutions of the g-Navier-Stokes equations[J]. Taiwanese J Math, 2004, 8(1): 85-102. [Google Scholar]
  19. Roh J. Dynamics of the g-Navier-Stokes equations[J]. Journal of Differential Equations, 2005, 211(2): 452-484. [Google Scholar]
  20. Kwak M, Kwean H, Roh J. The dimension of attractor of the 2D g-Navier-Stokes equations[J]. Journal of Mathematical Analysis and Applications, 2006, 315(2): 436-461. [Google Scholar]
  21. Jiang J P, Hou Y R. The global attractor of g-Navier-Stokes equations with linear dampness on 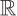Formula 2[J]. Applied Mathematics and Computation, 2009, 215(3): 1068-1076. [Google Scholar]
  22. Jiang J P, Hou Y R. Pullback attractor of 2D non-autonomous g-Navier-Stokes equations on some bounded domains[J]. Applied Mathematics and Mechanics (English Edition), 2010, 31(6): 697-708. [Google Scholar]
  23. Quyet D T. Pullback attractors for strong solutions of 2D non-autonomous g-Navier-Stokes equations[J]. Acta Mathematica Vietnamica, 2015, 40(4): 637-651. [Google Scholar]
  24. Wang X X, Jiang J P. The long-time behavior of 2D nonautonomous g-Navier-Stokes equations with weak dampness and time delay[J]. Journal of Function Spaces, 2022, 2022: 1-11. [Google Scholar]
  25. Wang X X, Jiang J P. The uniform asymptotic behavior of solutions for 2D g-Navier-Stokes equations with nonlinear dampness and its dimensions[J]. Electronic Research Archive, 2023, 31(7): 3963-3979. [Google Scholar]
  26. Wang X X, Jiang J P. The pullback attractor for the 2D g-Navier-Stokes equation with nonlinear damping and time delay[J]. AIMS Mathematics, 2023, 8(11): 26650-26664. [Google Scholar]
  27. Hale J K. Asymptotic Behaviour of Dissipative Dynamical Systems[M]. Providence: Amer Math Soc, 1988. [Google Scholar]
  28. Robinson J C. Infinite-Dimensional Dynamical Systems: An Introduction to Dissipative Parabolic PDEs and the Theory of Global Attractors[M]. Cambridge: Cambridge University Press, 2001. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.