| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
|
|
|---|---|---|
| Page(s) | 241 - 252 | |
| DOI | https://doi.org/10.1051/wujns/2025303241 | |
| Published online | 16 July 2025 | |
Mathematics
CLC number: O175
∑-Shaped Connected Component of Positive Solutions for One- Dimensional Prescribed Mean Curvature Equation in Minkowski Space
Minkowski 空间中一维给定平均曲率方程正解的∑-型连通分支
College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, Gansu, China
† Corresponding author. E-mail: luyq8610@126.com
Received:
5
December
2024
In this work, we demonstrate that the existence of an ∑-shaped connected component within the set of positive solutions for the one-dimensional prescribed mean curvature equation in Minkowski space 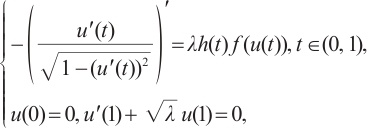 with boundary conditions having parameter in two cases
with boundary conditions having parameter in two cases 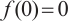 and
and 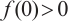 by using upper and lower solution method, where
by using upper and lower solution method, where 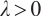 is a parameter,
is a parameter, 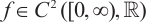 is monotonically increasing and
is monotonically increasing and 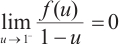 ,
, 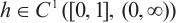 is a nonincreasing function and
is a nonincreasing function and 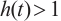 .
.
摘要
运用上下解方法证明 Minkowski 空间中一维给定平均曲率方程 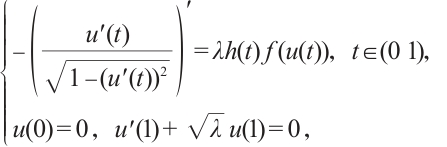
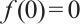 在 和
在 和 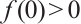 两种情形下正解集
两种情形下正解集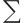 型连通分支的存在性,其中,
型连通分支的存在性,其中, 为参数,
为参数,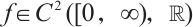 单调递增且满足
单调递增且满足 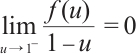 ,
,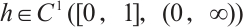 是单调递减函数且
是单调递减函数且 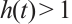 .
.
Key words: boundary conditions with parameters / positive solutions / the upper and lower solution method / asymptotic property
关键字 : 边界条件带参数 / 正解 / 上下解定理 / 渐进性质
Cite this article: QI Tiaoyan, LU Yanqiong. ∑-Shaped Connected Component of Positive Solutions for One- Dimensional Prescribed Mean Curvature Equation in Minkowski Space[J]. Wuhan Univ J of Nat Sci, 2025, 30(3): 241-252.
Biography: QI Tiaoyan, female, Master candidate, research direction: difference equations and their applications. E-mail: qity77@126.com
Foundation item: Supported by the National Natural Science Foundation of China (12361040)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


