| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
|
|
|---|---|---|
| Page(s) | 253 - 262 | |
| DOI | https://doi.org/10.1051/wujns/2025303253 | |
| Published online | 16 July 2025 | |
Mathematics
CLC number: O175.29
Study on the Density-Independent Fractional Diffusion-Reaction Equation with the Beta Derivative
带有beta导数的密度无关分数阶扩散反应方程研究
School of Statistics and Mathematics, Guangdong University of Finance and Economics, Guangzhou 510320, Guangdong, China
Received:
16
April
2024
In this paper, the density-independent fractional diffusion-reaction (FDR) equation involving quadratic nonlinearity is investigated. The fractional derivative is illustrated in the beta derivative sense. We firstly propose Bernoulli 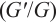 -expansion method to study nonlinear fractional differential equations (NFDEs). Subsequently, closed form solutions of the density-independent FDR equation are acquired successfully. In order to better understand the dynamic behaviors of these solutions, 3D, contour map and line plots are given by the computer simulation. The results show that the proposed method is a reliable and efficient approach.
-expansion method to study nonlinear fractional differential equations (NFDEs). Subsequently, closed form solutions of the density-independent FDR equation are acquired successfully. In order to better understand the dynamic behaviors of these solutions, 3D, contour map and line plots are given by the computer simulation. The results show that the proposed method is a reliable and efficient approach.
摘要
本文研究了涉及二次非线性的密度无关分数阶扩散反应方程。分数阶导数以beta导数的形式表示。首先,提出了Bernoulli 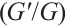 -展开法,并用其研究非线性分数阶微分方程。然后,获得了密度无关方程的精确解。为了更好地了解这些解的动力学行为,通过计算机仿真给出了三维图、等高线图和线图。结果表明,所提出的方法是一种可靠且高效的研究方法。
-展开法,并用其研究非线性分数阶微分方程。然后,获得了密度无关方程的精确解。为了更好地了解这些解的动力学行为,通过计算机仿真给出了三维图、等高线图和线图。结果表明,所提出的方法是一种可靠且高效的研究方法。
Key words: density-independent fractional diffusion-reaction (FDR) equation / beta derivative / closed form solutions / Bernoulli (G'/G)-expansion method
关键字 : 密度无关分数阶扩散反应方程 / beta导数 / 精确解 / Bernoulli (G'/G)-展开法
Cite this article: GU Yongyi, LAI Yongkang. Study on the Density-Independent Fractional Diffusion-Reaction Equation with the Beta Derivative[J]. Wuhan Univ J of Nat Sci, 2025, 30(3): 253-262.
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


