EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 30 / No 3 (June 2025) Wuhan Univ. J. Nat. Sci., 30 3 (2025) 253-262 References
Open Access
Issue
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
Page(s) 253 - 262
DOI https://doi.org/10.1051/wujns/2025303253
Published online 16 July 2025
  1. Liu J G, Ye Q. Stripe solitons and lump solutions for a generalized Kadomtsev-Petviashvili equation with variable coefficients in fluid mechanics[J]. Nonlinear Dynamics, 2019, 96(1): 23-29. [Google Scholar]
  2. Liu J G, Zhu W H, He Y. Variable-coefficient symbolic computation approach for finding multiple rogue wave solutions of nonlinear system with variable coefficients[J]. Zeitschrift Für Angewandte Mathematik Und Physik, 2021, 72(4): 154. [Google Scholar]
  3. Ozkan E M. New exact solutions of some important nonlinear fractional partial differential equations with beta derivative[J]. Fractal and Fractional, 2022, 6(3): 173. [Google Scholar]
  4. Tang B, He Y N, Wei L L, et al. A generalized fractional sub-equation method for fractional differential equations with variable coefficients[J]. Physics Letters A, 2012, 376(38-39): 2588-2590. [Google Scholar]
  5. Bekir A, Aksoy E, Cevikel A C. Exact solutions of nonlinear time fractional partial differential equations by sub-equation method[J]. Mathematical Methods in the Applied Sciences, 2015, 38(13): 2779-2784. [Google Scholar]
  6. Sooppy Nisar K, Enam Inan I, Inc M, et al. Properties of some higher-dimensional nonlinear Schrödinger equations[J]. Results in Physics, 2021, 31: 105073. [Google Scholar]
  7. Mirzazadeh M, Eslami M, Biswas A. Solitons and periodic solutions to a couple of fractional nonlinear evolution equations[J]. Pramana, 2014, 82(3): 465-476. [Google Scholar]
  8. Eslami M, Fathi Vajargah B, Mirzazadeh M, et al. Application of first integral method to fractional partial differential equations[J]. Indian Journal of Physics, 2014, 88(2): 177-184. [Google Scholar]
  9. Hosseini K, Mirzazadeh M, Baleanu D, et al. The generalized complex Ginzburg-Landau model and its dark and bright soliton solutions[J]. The European Physical Journal Plus, 2021, 136(7): 709. [Google Scholar]
  10. Hosseini K, Mirzazadeh M, Salahshour S, et al. Specific wave structures of a fifth-order nonlinear water wave equation[J]. Journal of Ocean Engineering and Science, 2022, 7(5): 462-466. [Google Scholar]
  11. Kaplan M, Bekir A. A novel analytical method for time-fractional differential equations[J]. Optik, 2016, 127(20): 8209-8214. [Google Scholar]
  12. Hosseini K, Bekir A, Ansari R. Exact solutions of nonlinear conformable time-fractional Boussinesq equations using the exp(-φ(z))-expansion method[J]. Optical and Quantum Electronics, 2017, 49(4): 131. [Google Scholar]
  13. Khan K, Ali Akbar M, Koppelaar H. Study of coupled nonlinear partial differential equations for finding exact analytical solutions[J]. Royal Society Open Science, 2015, 2(7): 140406. [Google Scholar]
  14. Zafar A, Raheel M, Asif M, et al. Some novel integration techniques to explore the conformable M-fractional Schrödinger-Hirota equation[J]. Journal of Ocean Engineering and Science, 2022, 7(4): 337-344. [Google Scholar]
  15. Nisar K S, Ali K K, Inc M, et al. New solutions for the generalized resonant nonlinear Schrödinger equation[J]. Results in Physics, 2022, 33: 105153. [Google Scholar]
  16. Sooppy Nisar K, Inan I E, Yepez-Martinez H, et al. Some new type optical and the other soliton solutions of coupled nonlinear Hirota equation[J]. Results in Physics, 2022, 35: 105388. [Google Scholar]
  17. Tariq H, Akram G. New approach for exact solutions of time fractional Cahn-Allen equation and time fractional Phi-4 equation[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 473: 352-362. [Google Scholar]
  18. Raslan K R, Ali K K, Shallal M A. The modified extended tanh method with the Riccati equation for solving the space-time fractional EW and MEW equations[J]. Chaos, Solitons & Fractals, 2017, 103: 404-409. [Google Scholar]
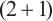  19. Hu H C, Li X D. New interaction solutions of the similarity reduction for the integrable Formula -dimensional Boussinesq equation[J]. International Journal of Modern Physics B, 2022, 36(1): 2250001. [Google Scholar]
  20. Kumar D, Hosseini K, Kaabar M K A, et al. On some novel solution solutions to the generalized Schrödinger-Boussinesq equations for the interaction between complex short wave and real long wave envelope[J]. Journal of Ocean Engineering and Science, 2022, 7(4): 353-362. [Google Scholar]
  21. Khater M M A, Jhangeer A, Rezazadeh H, et al. Propagation of new dynamics of longitudinal bud equation among a magneto-electro-elastic round rod[J]. Modern Physics Letters B, 2021, 35(35): 2150381. [Google Scholar]
  22. Kaplan, M, Bekir, A, Akbulut, A, et al. The modified simple equation method for nonlinear fractional differential equations. Romanian Journal of Physics, 2015, 60(9-10):1374. [Google Scholar]
  23. Kaplan M, Koparan M, Bekir A. Regarding on the exact solutions for the nonlinear fractional differential equations[J]. Open Physics, 2016, 14(1): 478-482. [Google Scholar]
  24. Rahman Z, Abdeljabbar A, Harun-Or-Roshid, et al. Novel precise solitary wave solutions of two time fractional nonlinear evolution models via the MSE scheme[J]. Fractal and Fractional, 2022, 6(8): 444. [Google Scholar]
  25. Gu Y Y, Yuan W J, Aminakbari N, et al. Meromorphic solutions of some algebraic differential equations related Painlevé equation IV and its applications[J]. Mathematical Methods in the Applied Sciences, 2018, 41(10): 3832-3840. [Google Scholar]
  26. Gu Y Y, Wu C F, Yao X, et al. Characterizations of all real solutions for the KdV equation and WR[J]. Applied Mathematics Letters, 2020, 107: 106446. [Google Scholar]
  27. Gu Y Y, Liao L W. Closed form solutions of Gerdjikov–Ivanov equation in nonlinear fiber optics involving the beta derivatives[J]. International Journal of Modern Physics B, 2022, 36(19): 2250116. [Google Scholar]
  28. Liu J G, Zhu W H, Wu Y K, et al. Application of multivariate bilinear neural network method to fractional partial differential equations[J]. Results in Physics, 2023, 47: 106341. [Google Scholar]
  29. Uddin M H, Akbar M A, Khan M A, et al. Close form solutions of the fractional generalized reaction duffing model and the density dependent fractional diffusion reaction equation[J]. Applied and Computational Mathematics, 2017, 6(4): 177-184. [Google Scholar]
  30. Hosseini K, Mayeli P, Bekir A, et al. Density-dependent conformable space-time fractional diffusion-reaction equation and its exact solutions[J]. Communications in Theoretical Physics, 2018, 69(1): 1. [Google Scholar]
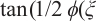  31. Rezazadeh H, Manafian J, Khodadad F S, et al. Traveling wave solutions for density-dependent conformable fractional diffusion-reaction equation by the first integral method and the improved Formula ))-expansion method[J]. Optical and Quantum Electronics, 2018, 50: 1-15. [Google Scholar]
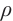  32. Sene N, Fall A N. Homotopy perturbation Formula -Laplace transform method and its application to the fractional diffusion equation and the fractional diffusion-reaction equation[J]. Fractal and Fractional, 2019, 3(2): 14. [Google Scholar]
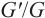  33. Wang M L, Li X Z, Zhang J L. The (Formula )-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics[J]. Physics Letters A, 2008, 372(4): 417-423. [Google Scholar]
  34. Kumar R, Kaushal R S, Prasad A. Some new solitary and travelling wave solutions of certain nonlinear diffusion-reaction equations using auxiliary equation method[J]. Physics Letters A, 2008, 372(19): 3395-3399. [Google Scholar]
  35. Kumar D, Seadawy A R, Joardar A K. Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology[J]. Chinese Journal of Physics, 2018, 56(1): 75-85. [Google Scholar]
  36. Murray J D. Mathematical Biology[M]. Heidelberg: Springer-Verlag, 1993. [Google Scholar]
  37. Kenkre V M, Kuperman M N. Applicability of the Fisher equation to bacterial population dynamics[J]. Physical Review E, 2003, 67(5): 051921. [Google Scholar]
  38. Atangana A, Doungmo Goufo E F. Extension of matched asymptotic method to fractional boundary layers problems[J]. Mathematical Problems in Engineering, 2014, 2014: 107535. [Google Scholar]
  39. Atangana A, Alqahtani R. Modelling the spread of river blindness disease via the caputo fractional derivative and the beta-derivative[J]. Entropy, 2016, 18(2): 40. [Google Scholar]
  40. Hosseini K, Mirzazadeh M, Gómez-Aguilar J F. Soliton solutions of the Sasa-Satsuma equation in the monomode optical fibers including the beta-derivatives[J]. Optik, 2020, 224: 165425. [Google Scholar]
  41. Hosseini K, Kaur L, Mirzazadeh M, et al. 1-Soliton solutions of the 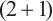Formula -dimensional Heisenberg ferromagnetic spin chain model with the beta time derivative[J]. Optical and Quantum Electronics, 2021, 53(2): 125. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.