EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 30 / No 3 (June 2025) Wuhan Univ. J. Nat. Sci., 30 3 (2025) 241-252 References
Open Access
Issue
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
Page(s) 241 - 252
DOI https://doi.org/10.1051/wujns/2025303241
Published online 16 July 2025
  1. Binding P A, Browne P J, Seddighi K. Sturm-Liouville problems with eigenparameter dependent boundary conditions[J]. Proceedings of the Edinburgh Mathematical Society, 1994, 37(1): 57-72. [Google Scholar]
  2. Hai D D. Positive solutions for semilinear elliptic equations in annular domains[J]. Nonl Anal: Theo, Meth & Appl, 1999, 37(9): 1051-1058. [Google Scholar]
  3. Marinets V V, Pitovka O Y. On a problem with a parameter in the boundary conditions[J]. Nauk Visn Uzhgorod Univ Ser Mat Inform, 2005 (10-11): 70-76. [Google Scholar]
  4. Li Z L. Second-order singular nonlinear boundary value problem with parameters in the boundary conditions[J]. Adv Math, 2008, 37(3): 353-360(Ch). [Google Scholar]
  5. Aslanova N, Bayramoglu M, Aslanov K. On one class eigenvalue problem with eigenvalue parameter in the boundary condition at one end-point[J]. Filomat, 2018, 32(19): 6667-6674. [Google Scholar]
  6. Fonseka N, Muthunayake A, Shivaji R, et al. Singular reaction diffusion equations where a parameter influences the reaction term and the boundary conditions[J]. Topological Methods in Nonlinear Analysis, 2021, 57(1): 221-242. [Google Scholar]
  7. Acharya A, Fonseka N, Quiroa J, et al. σ-shaped bifurcation curves[J]. Adv in Nonl Anal, 2021, 10(1): 1255-1266. [Google Scholar]
  8. Hai D D. Positive solutions to a class of elliptic boundary value problems[J]. J of Math Anal and Appl, 1998, 227(1): 195-199. [Google Scholar]
  9. Njoku F I, Omari P, Zanolin F. Multiplicity of positive radial solutions of a quasilinear elliptic problem in a ball[J]. Adv in Diff Equ, 2000, 5(10-12): 1545-1570. [Google Scholar]
  10. Bereanu C, Jebelean P, Mawhin J. Radial solutions for Neumann problems involving mean curvature operators in Euclidean and Minkowski spaces[J]. Mathematische Nachrichten, 2010, 283(3): 379-391. [Google Scholar]
  11. Jean M. Radial solutions of Neumann problem for periodic perturbations of the mean extrinsic curvature operator[J]. Milan Journal of Mathematics, 2011, 79(1): 95-112. [Google Scholar]
  12. Bartnik R, Simon L. Spacelike hypersurfaces with prescribed boundary values and mean curvature[J]. Communications in Mathematical Physics, 1982, 87(1): 131-152. [Google Scholar]
  13. Azzollini A. On a prescribed mean curvature equation in Lorentz-Minkowski space[J]. Journal de Mathématiques Pures et Appliquées, 2016, 106(6): 1122-1140. [Google Scholar]
  14. Born M, Infeld L. Foundations of the new field theory[J]. Nature, 1933, 132(3348): 1004. [Google Scholar]
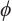  15. Bereanu C, Mawhin J. Existence and multiplicity results for some nonlinear problems with singular Formula -Laplacian[J]. J of Diff Equ, 2007, 243(2): 536-557. [Google Scholar]
  16. Anuradha V, Shivaji R. A quadrature method for classes of multi-parameter two point boundary value problems[J]. Applicable Analysis, 1994, 54(3-4): 263-281. [Google Scholar]
  17. Ma R Y, Lu Y Q. Multiplicity of positive solutions for second order nonlinear dirichlet problem with one-dimension Minkowski-curvature operator[J]. Adv Nonl Studies, 2015, 15(4): 789-803. [Google Scholar]
  18. Dai G W. Bifurcation and positive solutions for problem with mean curvature operator in Minkowski space[J]. Cal of Vari and Part Diff Equ, 2016, 55(4): 72. [Google Scholar]
  19. Xu M, Ma R Y. S-shaped connected component of radial positive solutions for a prescribed mean curvature problem in an annular domain[J]. Open Mathematics, 2008, 17: 929-941. [Google Scholar]
  20. Lu Y Q, Li Z Q, Chen T L. Multiplicity of solutions for non-homogeneous dirichlet problem with one-dimension minkowski-curvature operator[J]. Qualitative Theory of Dynamical Systems, 2022, 21(4): 145. [Google Scholar]
  21. Amann H. Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces[J]. SIAM Review, 1976, 18(4): 620-709. [Google Scholar]
  22. Dhanya R, Ko E, Shivaji R. A three solution theorem for singular nonlinear elliptic boundary value problems[J]. J of Math Anal and Appl, 2015, 424(1): 598-612. [Google Scholar]
  23. Gao H L, Xu J. Bifurcation curves and exact multiplicity of positive solutions for Dirichlet problems with the Minkowski-curvature equation[J]. Boundary Value Problems, 2021, 2021: 81. [Google Scholar]
  24. Goddard II J, Morris Q A, Robinson S B, et al. An exact bifurcation diagram for a reaction-diffusion equation arising in population dynamics[J]. Boundary Value Problems, 2018, 2018(1): 170. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.