Open Access
| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
|
|
|---|---|---|
| Page(s) | 235 - 240 | |
| DOI | https://doi.org/10.1051/wujns/2025303235 | |
| Published online | 16 July 2025 | |
- Galdi G P. An Introduction to the Mathematical Theory of the Navier-Stokes Equations: Steady-State Problems[M]. Second Edition. New York: Springer-Verlag, 2011. [Google Scholar]
-
Chae D, Wolf J. On Liouville type theorems for the steady Navier-Stokes equations in
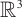 [J]. Journal of Differential Equations, 2016, 261(10): 5541-5560.
[Google Scholar]
[J]. Journal of Differential Equations, 2016, 261(10): 5541-5560.
[Google Scholar]
- Kozono H, Terasawa Y, Wakasugi Y. A remark on Liouville-type theorems for the stationary Navier-Stokes equations in three space dimensions[J]. Journal of Functional Analysis, 2017, 272(2): 804-818. [Google Scholar]
- Luo W, Yin Z Y. The Liouville theorem and the L2 decay for the FENE dumbbell model of polymeric flows[J]. Archive for Rational Mechanics and Analysis, 2017, 224(1): 209-231. [Google Scholar]
- Chae D. Liouville-type theorems for the forced Euler equations and the Navier-Stokes equations[J]. Communications in Mathematical Physics, 2014, 326(1): 37-48. [Google Scholar]
- Chae D, Yoneda T. On the Liouville theorem for the stationary Navier-Stokes equations in a critical space[J]. Journal of Mathematical Analysis and Applications, 2013, 405(2): 706-710. [Google Scholar]
- Superiore S, Gilbarg D, Weinberger H, et al. Asymptotic properties of steady plane solutions of the Navier-Stokes equations with bounded Dirichlet integral[J]. Annali Della Scuola Normale Superiore Di Pisa-classe Di Scienze, 1978, 5: 381-404. [Google Scholar]
- Koch G, Nadirashvili N, Seregin G A, et al. Liouville theorems for the Navier-Stokes equations and applications[J]. Acta Mathematica, 2009, 203(1): 83-105. [Google Scholar]
- Korobkov M, Pileckas K, Russo R. The Liouville theorem for the steady-state Navier-Stokes problem for axially symmetric 3D solutions in absence of swirl[J]. Journal of Mathematical Fluid Mechanics, 2015, 17(2): 287-293. [Google Scholar]
- Gong H J, Liu X G, Zhang X T. Liouville theorem for the steady-state solutions of Q-tensor system of liquid crystal[J]. Applied Mathematics Letters, 2018, 76: 175-180. [Google Scholar]
- Lai N, Wu J. A note on Liouville theorem for steady Q-tensor system of liquid crystal[J]. Journal of Zhejiang University (Science Edition), 2022, 49(4): 418-421(Ch). [Google Scholar]
- Schulz S. Liouville-type theorem for the stationary equations of magnetohydrodynamics[J]. Acta Mathematica Scientia, 2019, 39(2): 491-497. [Google Scholar]
- Wu F. Liouville-type theorems for the 3D compressible magnetohydrodynamics equations[J]. Nonlinear Analysis: Real World Applications, 2022, 64: 103429. [Google Scholar]
- Yuan B Q, Xiao Y M. Liouville-type theorems for the 3D stationary Navier-Stokes, MHD and Hall-MHD equations[J]. Journal of Mathematical Analysis and Applications, 2020, 491(2): 124343. [Google Scholar]
- Yuan B, Wang F. The Liouville theorems for 3D stationary tropical climate model in local Morrey spaces[J]. Applied Mathematics Letters, 2023, 138: 108533. [Google Scholar]
- Jarrín O. A remark on the Liouville problem for stationary Navier-Stokes equations in Lorentz and Morrey spaces[J]. Journal of Mathematical Analysis and Applications, 2020, 486(1): 123871. [Google Scholar]
- Majumdar A. Equilibrium order parameters of nematic liquid crystals in the Landau-de Gennes theory[J]. European Journal of Applied Mathematics, 2010, 21(2): 181-203. [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


