EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 30 / No 3 (June 2025) Wuhan Univ. J. Nat. Sci., 30 3 (2025) 231-234 References
Open Access
Issue
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
Page(s) 231 - 234
DOI https://doi.org/10.1051/wujns/2025303231
Published online 16 July 2025
  1. Hou X D. Permutation polynomials over finite fields: A survey of recent advances[J]. Finite Fields and Their Applications, 2015, 32: 82-119. [Google Scholar]
  2. Li N, Zeng X Y. A survey on the applications of niho exponents[J]. Cryptography and Communications, 2019, 11(3): 509-548. [Google Scholar]
  3. Wang Q. Combinatorics and Finite Fields[M]. Berlin: De Gruyter, 2019. [Google Scholar]
  4. Kyureghyan G, Zieve M. Contemporary Developments in Finite Fields and Applications[M]. Singapore: World Scientific, 2016. [Google Scholar]
  5. Zheng D B, Yuan M, Yu L. Two types of permutation polynomials with special forms[J]. Finite Fields and Their Applications, 2019, 56: 1-16. [Google Scholar]
  6. Qin X E, Yan L. Constructing permutation trinomials via monomials on the subsets of μq+1[J]. Applicable Algebra in Engineering, Communication and Computing, 2021, 34(2): 321-334. [Google Scholar]
  7. Lavorante V P. New families of permutation trinomials constructed by permutations of μq+1[EB/OL]. [2023-2-15]. https://arxiv.org/abs/2105.12012. [Google Scholar]
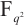  8. Hou X D, Lavorante V. P. A general construction of permutation polynomials of Formula [J]. Finite Fields Appl, 2023, 89: 102193. [Google Scholar]
  9. Gupta R. Several new permutation quadrinomials over finite fields of odd characteristic[J]. Designs, Codes and Cryptography, 2020, 88(1): 223-239. [Google Scholar]
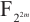  10. Tu Z, Zeng X Y, Helleseth T. New permutation quadrinomials over Formula [J]. Finite Fields Appl, 2018, 50: 304-318. [Google Scholar]
  11. Tu Z R, Zeng X Y, Helleseth T. A class of permutation quadrinomials[J]. Discrete Mathematics, 2018, 341(11): 3010-3020. [Google Scholar]
  12. Zheng L J, Liu B X, Kan H B, et al. More classes of permutation quadrinomials from Niho exponents in characteristic two[J]. Finite Fields and Their Applications, 2022, 78: 101962. [Google Scholar]
  13. Pallozzi Lavorante V P. On permutation quadrinomials from Niho exponents in characteristic two[J]. Finite Fields and Their Applications, 2024, 96: 102418. [Google Scholar]
  14. Ding Z G, Zieve M E. Determination of a class of permutation quadrinomials[J]. Proceedings of the London Mathematical Society, 2023, 127(2): 221-260. [Google Scholar]
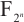  15. Brochero Martínez F E, Gupta R, Quoos L. Classification of some permutation quadrinomials from self reciprocal polynomials over Formula [J]. Finite Fields and Their Applications, 2023, 91: 102276. [Google Scholar]
  16. Akbary A, Wang Q. On polynomials of the form xrf(xq-1/l)[J]. Int J Math Math Sci, 2007, 2007: 23408. [Google Scholar]
  17. Wang Q. Cyclotomic mapping permutation polynomials over finite fields[C]//Sequences, Subsequences, and Consequences. Berlin: Springer-Verlag, 2007: 119-128. [Google Scholar]
  18. Li K Q, Qu L J, Chen X, et al. Permutation polynomials of the form 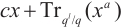Formula and permutation trinomials over finite fields with even characteristic[J]. Cryptography and Communications, 2018, 10(3): 531-554. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.