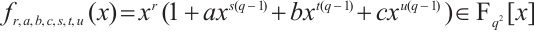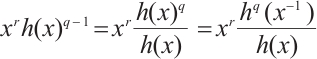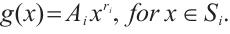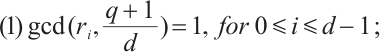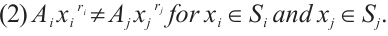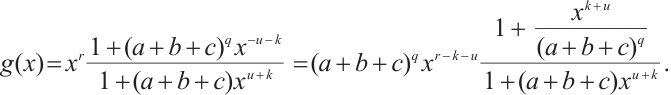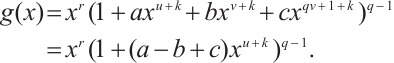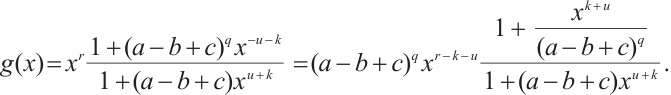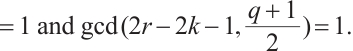| Issue |
Wuhan Univ. J. Nat. Sci.
Volume 30, Number 3, June 2025
|
|
|---|---|---|
| Page(s) | 231 - 234 | |
| DOI | https://doi.org/10.1051/wujns/2025303231 | |
| Published online | 16 July 2025 | |
Mathematics
CLC number: O156.1
A Note on a Class of Permutation Quadrinomials of Fq2
有限域上一类置换四项式的注记
1 School of Mathematics and Big Data, Chongqing University of Education, Chongqing 400065, China
2 School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China
† Corresponding author. E-mail: yanl930@163.com
Received:
15
July
2024
Constructing permutation polynomials is a hot topic in finite fields, and permutation polynomials have many applications in different areas. In this paper, by using monomials on the cosets of a subgroup to characterize the permutational property of rational functions on 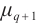 , we construct a class of permutation quadrinomials with the form
, we construct a class of permutation quadrinomials with the form 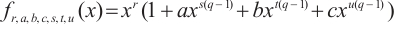 of
of 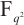 .
.
摘要
构造置换多项式是有限域上的一个热点问题,置换多项式在诸多领域都有应用。本文利用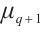 的子群陪集上的单项式来刻画
的子群陪集上的单项式来刻画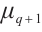 上有理函数的置换性质,构造了一类有限域
上有理函数的置换性质,构造了一类有限域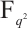 上形如
上形如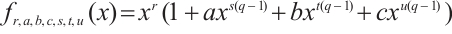 的置换四项式。
的置换四项式。
Key words: permutation quadrinomials / monomials / finite fields
关键字 : 置换四项式 / 单项式 / 有限域
Cite this article: QIN Xiaoer, GUO Xiaonan, QIU Yinuo, et al. A Note on a Class of Permutation Quadrinomials of Fq2[J]. Wuhan Univ J of Nat Sci, 2025, 30(3): 231-234.
Biography: QIN Xiaoer, male, Ph.D., research direction: number theory. E-mail: qincn328@sina.com
Foundation item: Supported by the National Natural Science Foundation of China (11926344), Science and Technology Research Program of Chongqing Municipal Education Commission (KJZD-K202401601), Doctor Talent Program of Chongqing University of Education (2023BSRC003) and Undergraduate Science Research Program of Chongqing University of Education (KY20240046)
© Wuhan University 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0 Introduction
Let 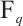 be the finite field with
be the finite field with 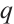 elements. A polynomial
elements. A polynomial  is called a permutation polynomial if
is called a permutation polynomial if 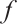 induces a bijection from
induces a bijection from 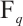 to itself. Permutation polynomials have wide applications in coding theory, cryptography and combinatorial designs. We refer the readers to Refs. [1-3] for more details of the recent advances.
to itself. Permutation polynomials have wide applications in coding theory, cryptography and combinatorial designs. We refer the readers to Refs. [1-3] for more details of the recent advances.
Permutation polynomials with a few terms have attracted more attention in recent years for their simple algebraic forms and some special properties. There are several classes of permutation trinomials of the form 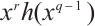 over
over 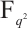 constructed in recent years. Kyureghyan and Zieve[4] described a class of permutation trinomials having the form
constructed in recent years. Kyureghyan and Zieve[4] described a class of permutation trinomials having the form 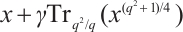 of
of 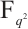 , where
, where 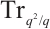 is the trace function from
is the trace function from 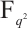 to
to 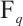 . We note that this kind of permutation trinomials actually has the form
. We note that this kind of permutation trinomials actually has the form 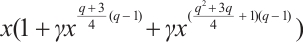 . Zheng et al[5] showed a class of permutation trinomials of the form
. Zheng et al[5] showed a class of permutation trinomials of the form 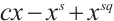 , where
, where 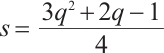 , which can be rewritten as
, which can be rewritten as 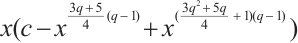 . In Ref. [6], the authors got several classes of more generalized permutation trinomials having similar forms to
. In Ref. [6], the authors got several classes of more generalized permutation trinomials having similar forms to 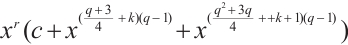
and 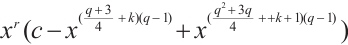 . By using a similar idea to Ref. [6], Lavorante[7] constructed a few new families of permutation trinomials with the form
. By using a similar idea to Ref. [6], Lavorante[7] constructed a few new families of permutation trinomials with the form 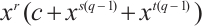 . By using monomial functions on the cosets of a subgroup of
. By using monomial functions on the cosets of a subgroup of 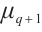 , Hou and Lavorante[8] gave a general method to construct permutation polynomials over
, Hou and Lavorante[8] gave a general method to construct permutation polynomials over 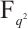 . Specially, they presented several classes of permutation binomials and trinomials.
. Specially, they presented several classes of permutation binomials and trinomials.
On the other hand, permutation quadrinomials also have attracted attention in recent years. Especially, constructing permutation quadrinomials of the form
where 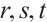 are integers, attracted great interest recently. Gupa[9] studied several classes of permutation quadrinomials of the form (1) over
are integers, attracted great interest recently. Gupa[9] studied several classes of permutation quadrinomials of the form (1) over 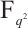 with
with 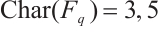 . Tu et al[10] proposed a class of permutation quadrinomials having the form
. Tu et al[10] proposed a class of permutation quadrinomials having the form 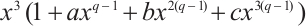 of
of 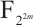 . In Ref. [11], the authors investigated some permutation quadrinomials of
. In Ref. [11], the authors investigated some permutation quadrinomials of 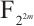 with the case of
with the case of 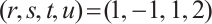 in (1) under some restrictive conditions. In Ref. [12], the authors provided more classes of permutation quadrinomials of the form (1) in characteristic two. Lavorante[13] used the Hasse-Weil type theorems to prove the necessary conditions for a polynomial in Ref. [12] to be a permutation polynomial. Ding and Zieve[14] determined all permutation polynomials over
in (1) under some restrictive conditions. In Ref. [12], the authors provided more classes of permutation quadrinomials of the form (1) in characteristic two. Lavorante[13] used the Hasse-Weil type theorems to prove the necessary conditions for a polynomial in Ref. [12] to be a permutation polynomial. Ding and Zieve[14] determined all permutation polynomials over 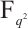 having the form
having the form 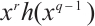 , where, for some
, where, for some 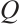 which is the power of the character of
which is the power of the character of 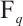 , the terms of
, the terms of 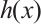 have degrees
have degrees 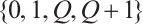 and
and 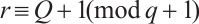 . The authors in Ref. [15] characterized two classes of permutation quadrinomials over
. The authors in Ref. [15] characterized two classes of permutation quadrinomials over 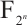 by using self-reciprocal polynomials. In this paper, motivated by the method in Ref. [6], we continue to construct a new class of permutation quadrinomials of
by using self-reciprocal polynomials. In this paper, motivated by the method in Ref. [6], we continue to construct a new class of permutation quadrinomials of 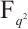 .
.
This paper is organized as follows: In Section 1, we list some results, which will be used in our paper. In Section 2, by using monomials of 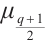 and
and 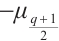 , we construct a class of permutation quadrinomials over
, we construct a class of permutation quadrinomials over 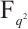 of the form
of the form  for some integers
for some integers 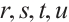 .
.
1 Preliminary
The following result was discovered independently by several authors.
Lemma 1[16-17]
Let 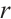 be a positive integer. Then
be a positive integer. Then 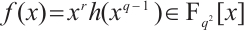 is a permutation polynomial of
is a permutation polynomial of 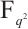 if and only if each of the following is true:
if and only if each of the following is true:
(1) 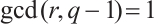 ,
,
(2) 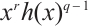 permutes
permutes 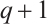 -th roots of unity
-th roots of unity 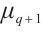 .
.
Specially, by using Lemma 1, constructing permutation polynomials of the form 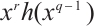 over
over 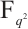 translates to finding permutations having the form
translates to finding permutations having the form 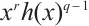 on the set of
on the set of 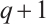 -th roots of unity
-th roots of unity 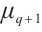 . For
. For 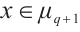 , one has
, one has
where 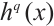 denotes the polynomial obtained
denotes the polynomial obtained 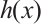 by raising every coefficient to the
by raising every coefficient to the 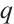 -th power. Thus to show that
-th power. Thus to show that 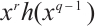 permutes
permutes 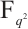 , the point is to prove that the rational function
, the point is to prove that the rational function 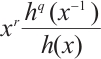 permutes
permutes 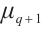 .
.
Let 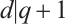 with
with 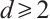 be a positive integer and
be a positive integer and 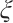 be a primitive
be a primitive 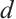 -th root of unity. We make some denotations:
-th root of unity. We make some denotations: 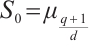 and
and 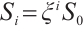 for
for 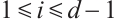 . It is easy to imply that
. It is easy to imply that 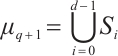 and
and 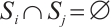 for
for 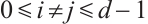 .
.
For 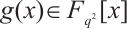 , if
, if 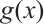 is a monomial on each subset of
is a monomial on each subset of 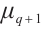 , then by using the piecewise method, we can easily determine the permutational property of
, then by using the piecewise method, we can easily determine the permutational property of 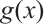 on
on 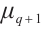 in the following lemma.
in the following lemma.
Lemma 2[6] Let 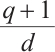 be a positive integer and
be a positive integer and 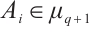 for
for 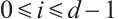 . For
. For 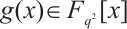 , if
, if
Then 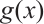 permutes
permutes 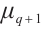 if and only if each of the following is true:
if and only if each of the following is true:
Lemma 2 provides an approach to study the permutational property of 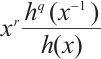 on
on 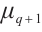 via monomials on the subsets
via monomials on the subsets 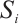 . In Refs. [4,5,7], the authors used the case
. In Refs. [4,5,7], the authors used the case 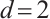 in Lemma 2 to construct a few classes of permutation trinomials of
in Lemma 2 to construct a few classes of permutation trinomials of 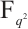 . By using the cases
. By using the cases 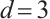 , the authors obtained several kinds of permutation trinomials of
, the authors obtained several kinds of permutation trinomials of 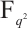 in Refs. [16,18].
in Refs. [16,18].
2 Main Results
Motivated by the method in Ref. [6], we characterize several classes of permutation quadrinomials over 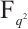 in this section.
in this section.
Theorem 1 Let 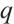 be a prime power with
be a prime power with 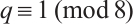 , and
, and 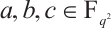 satisfy
satisfy 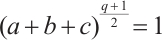 and
and 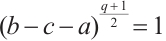 . Let
. Let  be a positive integer and
be a positive integer and  be an even integer. Then
be an even integer. Then 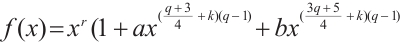
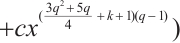 permutes
permutes 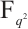 if and only if
if and only if  and
and 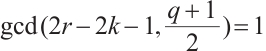 .
.
Proof It follows from Lemma 1 that 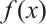 permutes
permutes 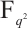 if and only if
if and only if 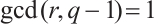 and
and 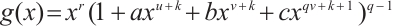 permutes
permutes 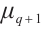 , where
, where 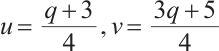 .
.
In the following, we claim that if 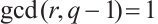 , then
, then 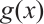 permutes
permutes 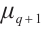 if and only if
if and only if 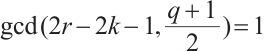 .
.
We divide 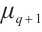 into two subsets
into two subsets 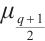 and
and 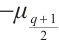 , and consider the following cases. For
, and consider the following cases. For  in
in 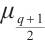 , it is easy to check that
, it is easy to check that 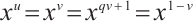 . One has
. One has 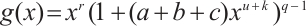 .
.
Since 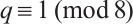 , we have that
, we have that 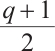 is odd. Then by
is odd. Then by 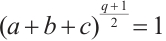 , we deduce that the equation
, we deduce that the equation 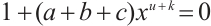 has no roots in
has no roots in 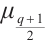 . Furthermore,
. Furthermore,
By using 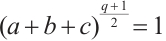 ,
, 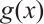 can be simplified as
can be simplified as 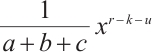 . Since
. Since 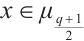 can be written as
can be written as 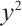 for
for 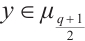 and
and 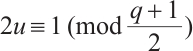 , thus
, thus 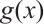 can be rewritten as
can be rewritten as 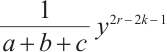 .
.
For 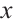 in
in 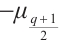 , one has
, one has 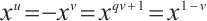 . Then
. Then
Since 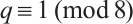 , we have that
, we have that 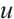 and
and 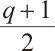 are odd, thus
are odd, thus 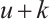 is odd. Then by
is odd. Then by 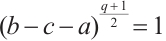 , we know that
, we know that 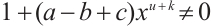 for
for 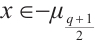 . Thus
. Thus
Since 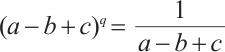 and
and 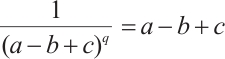 , then
, then 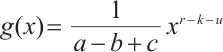 . For
. For 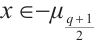 , there exists
, there exists 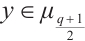 such that
such that 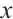 can be presented by
can be presented by 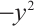 . Then
. Then 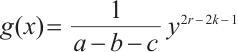 .
.
Note that 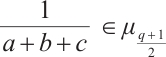 and
and 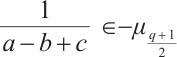 . Then it follows from Lemma 2 that
. Then it follows from Lemma 2 that 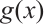 permutes
permutes 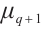 if and only if
if and only if 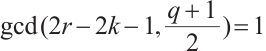 . Namely, the claim is true.
. Namely, the claim is true.
Therefore, we can conclude that 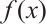 permutes
permutes 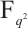 if and only if
if and only if 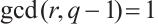 and
and 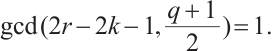
We complete the proof of Theorem 1.
Similarly, we can get the following results, and we omit their detailed proofs.
Theorem 2 Let 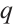 be a prime power with
be a prime power with 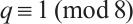 , and
, and 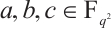 satisfy
satisfy 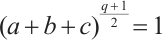 and
and 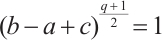 . Let
. Let 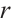 be a positive integer and
be a positive integer and 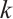 be an even integer. Then
be an even integer. Then 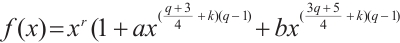
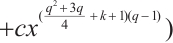 permutes
permutes 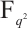 if and only if
if and only if 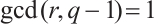 and
and 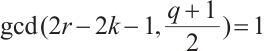 .
.
Theorem 3 Let 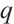 be a prime power with
be a prime power with 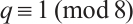 , and
, and 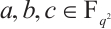 satisfy
satisfy 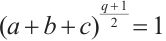 and
and 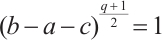 . Let
. Let 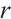 be a positive integer and
be a positive integer and 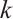 be an even integer. Then
be an even integer. Then 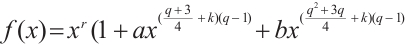
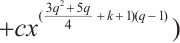 permutes
permutes 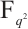 if and only if
if and only if 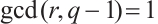 and
and 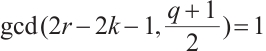 .
.
Theorem 4 Let 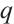 be a prime power with
be a prime power with 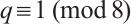 , and
, and 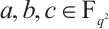 satisfy
satisfy 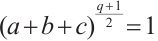 and
and 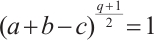 . Let
. Let 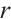 be a positive integer and
be a positive integer and 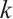 be an even integer. Then
be an even integer. Then 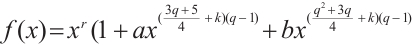
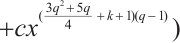 permutes
permutes 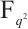 if and only if
if and only if 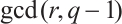
References
- Hou X D. Permutation polynomials over finite fields: A survey of recent advances[J]. Finite Fields and Their Applications, 2015, 32: 82-119. [Google Scholar]
- Li N, Zeng X Y. A survey on the applications of niho exponents[J]. Cryptography and Communications, 2019, 11(3): 509-548. [Google Scholar]
- Wang Q. Combinatorics and Finite Fields[M]. Berlin: De Gruyter, 2019. [Google Scholar]
- Kyureghyan G, Zieve M. Contemporary Developments in Finite Fields and Applications[M]. Singapore: World Scientific, 2016. [Google Scholar]
- Zheng D B, Yuan M, Yu L. Two types of permutation polynomials with special forms[J]. Finite Fields and Their Applications, 2019, 56: 1-16. [Google Scholar]
- Qin X E, Yan L. Constructing permutation trinomials via monomials on the subsets of μq+1[J]. Applicable Algebra in Engineering, Communication and Computing, 2021, 34(2): 321-334. [Google Scholar]
- Lavorante V P. New families of permutation trinomials constructed by permutations of μq+1[EB/OL]. [2023-2-15]. https://arxiv.org/abs/2105.12012. [Google Scholar]
-
Hou X D, Lavorante V. P. A general construction of permutation polynomials of
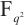 [J]. Finite Fields Appl, 2023, 89: 102193.
[Google Scholar]
[J]. Finite Fields Appl, 2023, 89: 102193.
[Google Scholar]
- Gupta R. Several new permutation quadrinomials over finite fields of odd characteristic[J]. Designs, Codes and Cryptography, 2020, 88(1): 223-239. [Google Scholar]
-
Tu Z, Zeng X Y, Helleseth T. New permutation quadrinomials over
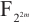 [J]. Finite Fields Appl, 2018, 50: 304-318.
[Google Scholar]
[J]. Finite Fields Appl, 2018, 50: 304-318.
[Google Scholar]
- Tu Z R, Zeng X Y, Helleseth T. A class of permutation quadrinomials[J]. Discrete Mathematics, 2018, 341(11): 3010-3020. [Google Scholar]
- Zheng L J, Liu B X, Kan H B, et al. More classes of permutation quadrinomials from Niho exponents in characteristic two[J]. Finite Fields and Their Applications, 2022, 78: 101962. [Google Scholar]
- Pallozzi Lavorante V P. On permutation quadrinomials from Niho exponents in characteristic two[J]. Finite Fields and Their Applications, 2024, 96: 102418. [Google Scholar]
- Ding Z G, Zieve M E. Determination of a class of permutation quadrinomials[J]. Proceedings of the London Mathematical Society, 2023, 127(2): 221-260. [Google Scholar]
-
Brochero Martínez F E, Gupta R, Quoos L. Classification of some permutation quadrinomials from self reciprocal polynomials over
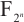 [J]. Finite Fields and Their Applications, 2023, 91: 102276.
[Google Scholar]
[J]. Finite Fields and Their Applications, 2023, 91: 102276.
[Google Scholar]
- Akbary A, Wang Q. On polynomials of the form xrf(xq-1/l)[J]. Int J Math Math Sci, 2007, 2007: 23408. [Google Scholar]
- Wang Q. Cyclotomic mapping permutation polynomials over finite fields[C]//Sequences, Subsequences, and Consequences. Berlin: Springer-Verlag, 2007: 119-128. [Google Scholar]
-
Li K Q, Qu L J, Chen X, et al. Permutation polynomials of the form
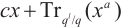 and permutation trinomials over finite fields with even characteristic[J]. Cryptography and Communications, 2018, 10(3): 531-554.
[Google Scholar]
and permutation trinomials over finite fields with even characteristic[J]. Cryptography and Communications, 2018, 10(3): 531-554.
[Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.